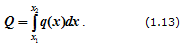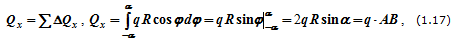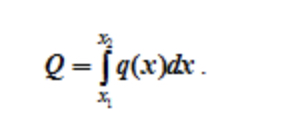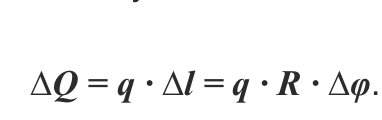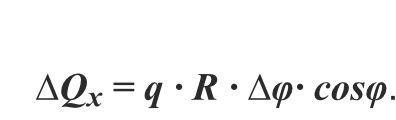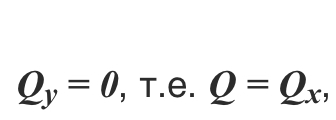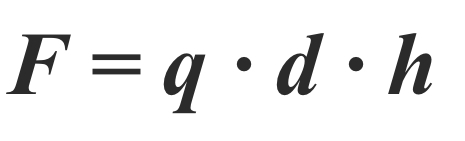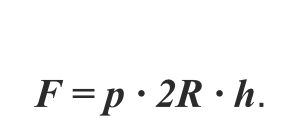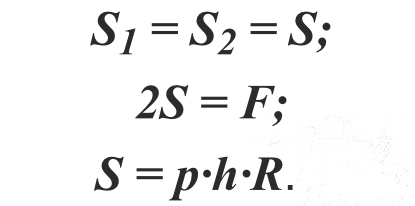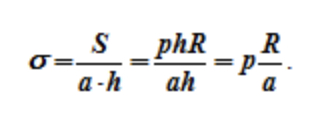что такое равномерно распределенная нагрузка
iSopromat.ru
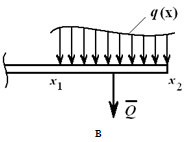
Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены не в одной точке твердого тела (т.е. не сосредоточены в одной точке), а равномерно, случайным образом или по заданному закону распределены по его определенной длине, площади или объему.
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
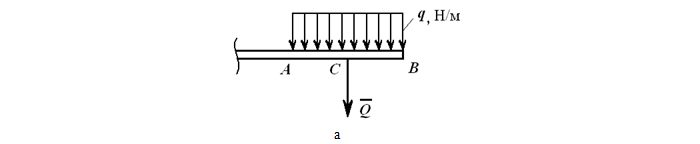
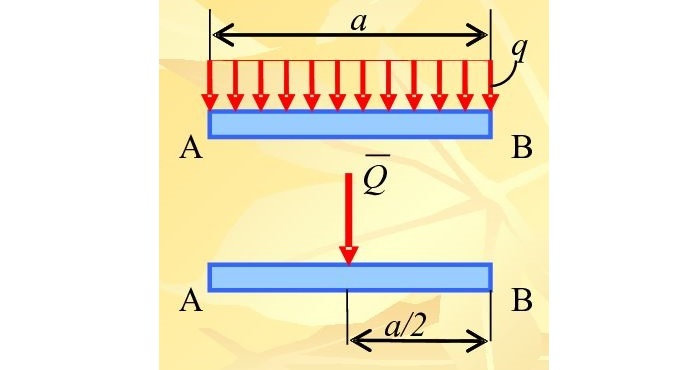
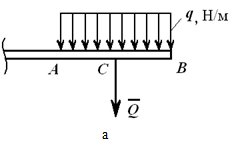
Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
приложенной в середине отрезка AB.
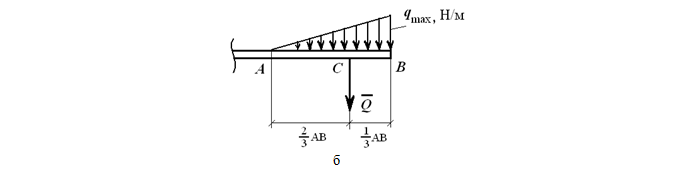
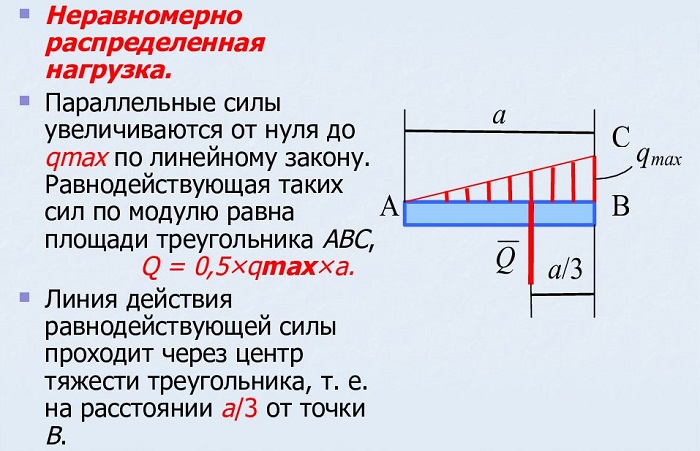
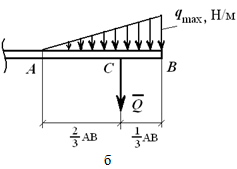
На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
приложенной в точке C, причем AC = 2/3AB.
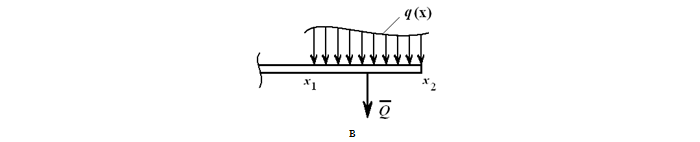
В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу
Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).
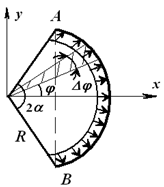
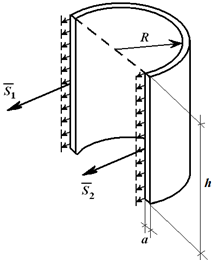
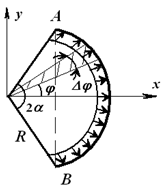
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).
Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:
В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:
где АВ – хорда, стягивающая концы дуги.
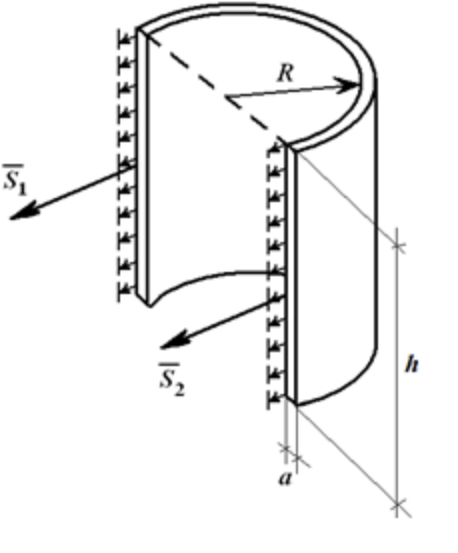
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м, 2 ]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q ∙ d ∙ h ( d – внутренний диаметр) или
Разрывающие баллон по диаметру усилия:
Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Равномерно распределенная нагрузка
Равномерно распределенная нагрузка – распределенная нагрузка постоянной интенсивности на единицу длины (площади поверхности).
[Отраслевой руководящий документ. Техническая эксплуатация железобетонных конструкций производственных зданий. Часть1. г. Москва 1993 г.]
Полезное
Смотреть что такое «Равномерно распределенная нагрузка» в других словарях:
равномерно распределенная нагрузка — Распределенная нагрузка постоянной интенсивности на единицу длины (площади поверхности). [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Лотки в… … Справочник технического переводчика
равномерно распределенная нагрузка (в строительной механике) — равномерно распределенная нагрузка Распределенная нагрузка постоянной интенсивности на единицу длины (площади поверхности). [http://www.isopromat.ru/sopromat/terms] Тематики строительная механика, сопротивление материалов EN continuous load … Справочник технического переводчика
равномерно распределенная нагрузка; РРН — 3.18 равномерно распределенная нагрузка; РРН (uniformly distributed load; UDL): Нагрузка, распределенная равномерно в пределах данной площади. Примечание Методы приложения равномерно распределенной нагрузки приведены в приложениях D, F. Источник … Словарь-справочник терминов нормативно-технической документации
Нагрузка равномерно распределенная — – нагрузка постоянной интенсивности, прилагаемая непрерывно к данной поверхности (линии) или части ее. [СНиП I 2] Рубрика термина: Виды нагрузок на материалы Рубрики энциклопедии: Абразивное оборудование, Абразивы, Автодороги … Энциклопедия терминов, определений и пояснений строительных материалов
Нагрузка равномерно распределенная — распределенная нагрузка постоянной интенсивности на единицу длины (площади) поверхности. Источник: Справочник дорожных терминов … Строительный словарь
НАГРУЗКА ЭКВИВАЛЕНТНАЯ — сплошная равномерно распределенная нагрузка, к рая в данном элементе сооружения (напр. моста) вызывает такое же усилие, как и соответствующие ей сосредоточенные грузы (напр. давления колес поезда). Величина Н. э. зависит от схемы поезда,… … Технический железнодорожный словарь
НАГРУЗКА ПОСТОЯННАЯ — нагрузка, беспрерывно действующая на сооружение, как, напр., собственный вес элементов конструкции, давление земли на устои мостов и др. Величина собственного веса, являющегося постоянной вертикальной нагрузкой, подсчитывается в соответствии с… … Технический железнодорожный словарь
Нагрузка эквивалентная — условная, равномерно распределенная по длине сооружения нагрузка, действие которой вызывают в рассматриваемом сечении конструкции усилия, равные усилиям от действительной нагрузки. Источник: Справочник дорожных терминов … Строительный словарь
ГОСТ Р 52868-2007: Системы кабельных лотков и системы кабельных лестниц для прокладки кабелей. Общие технические требования и методы испытаний — Терминология ГОСТ Р 52868 2007: Системы кабельных лотков и системы кабельных лестниц для прокладки кабелей. Общие технические требования и методы испытаний оригинал документа: 3.10 аксессуар системы (system accessory): Компонент системы,… … Словарь-справочник терминов нормативно-технической документации
Виды нагрузок на материалы — Термины рубрики: Виды нагрузок на материалы Воздействие силовое Динамическая нагрузка Интенсивность нагрузки Коэффициент надежности по нагрузке … Энциклопедия терминов, определений и пояснений строительных материалов
СП 20.13330.2011 Нагрузки и воздействия. Актуализированная редакция СНиП 2.01.07-85*
8.2 Равномерно распределенные нагрузки
8.2.1 Нормативные значения равномерно распределенных временных нагрузок на плиты перекрытий, лестницы и полы на грунтах приведены в таблице 8.3.
Помещения зданий и сооружений
Квартиры жилых зданий; спальные помещения детских дошкольных учреждений и школ-интернатов; жилые помещения домов отдыха и пансионатов, общежитий и гостиниц; палаты больниц и санаториев; террасы
Служебные помещения административного, инженерно-технического, научного персонала организаций и учреждений; офисы, классные помещения учреждений просвещения; бытовые помещения (гардеробные, душевые, умывальные, уборные) промышленных предприятий и общественных зданий и сооружений
Кабинеты и лаборатории учреждений здравоохранения, лаборатории учреждений просвещения, науки; помещения электронно-вычислительных машин; кухни общественных зданий; помещения учреждений бытового обслуживания населения (парикмахерские, ателье и т.п.); технические этажи жилых и общественных зданий высотой менее 75 м; подвальные помещения
б) обеденные (в кафе, ресторанах, столовых и т.п.)
в) собраний и совещаний, ожидания, зрительные и концертные, спортивные, фитнес-центры, бильярдные
г) торговые, выставочные и экспозиционные
Сцены зрелищных предприятий
а) с закрепленными сиденьями
б) для стоящих зрителей
Покрытия на участках:
а) с возможным скоплением людей (выходящих из производственных помещений, залов, аудиторий и т.п.)
б) используемых для отдыха
Балконы (лоджии) с учетом нагрузки:
а) полосовой равномерной на участке шириной 0,8 м вдоль ограждения балкона (лоджии)
б) сплошной равномерной на площади балкона (лоджии), воздействие которой не благоприятнее, чем определяемое по 10, а
Участки обслуживания и ремонта оборудования в производственных помещениях
Вестибюли, фойе, коридоры, лестницы (с относящимися к ним проходами), примыкающие к помещениям, указанным в позициях:
Помещения для скота:
1 Нагрузки, указанные в поз.8, следует учитывать на площади, не занятой оборудованием и материалами.
2 Нагрузки, указанные в поз.9, не следует учитывать одновременно со снеговой нагрузкой.
3 Нагрузки, указанные в поз.10, следует учитывать при расчете несущих конструкции балконов (лоджий) и участков стен в местах защемления этих конструкций. При расчете нижележащих участков стен, фундаментов и оснований нагрузки на балконы (лоджии) следует принимать равными нагрузкам примыкающих основных помещений зданий и снижать их с учетом указаний 8.2.4 и 8.2.5.
4 Нормативные значения нагрузок для зданий и помещений, указанных в позициях 3, 4г, 5, 6, 11 и 14, следует принимать по строительному заданию на основании технологических решений.
8.2.2 Нормативные значения нагрузок на ригели и плиты перекрытий от веса временных перегородок следует принимать в зависимости от их конструкции, расположения и характера опирания на перекрытия и стены. Указанные нагрузки допускается учитывать как равномерно распределенные добавочные нагрузки, принимая их нормативные значения на основании расчета для предполагаемых схем размещения перегородок, но не менее 0,5 кПа.
Коэффициенты надежности по нагрузке для равномерно распределенных нагрузок следует принимать:
Коэффициент надежности по нагрузке от веса временных перегородок следует принимать в соответствии с указаниями 7.2.
8.2.3 Пониженные нормативные значения равномерно распределенных нагрузок (см. позицию 4) определяются умножением их нормативных значений на коэффициент 0,35. Для нагрузок, указанных в позициях 5, 8, 9, в и 11 таблицы 8.3, пониженные значения не устанавливаются.
а) для помещений, указанных в позициях 1, 2, 12, а (при 

б) для помещений, указанных в позициях 4, 11, 12, б (при 

8.2.5 При определении усилий для расчета колонн, стен и фундаментов, воспринимающих нагрузки от двух перекрытий и более, полные нормативные значения нагрузок, указанные в позициях 1, 2, 4, 11, 12, а и 12, б таблицы 8.3, допускается снижать умножением на коэффициенты сочетания или :
а) для помещений, указанных в позициях 1, 2, 12, а

б) для помещений, указанных в позициях 4, 11, 12, б

— общее число перекрытий, нагрузки от которых учитываются при расчете рассматриваемого сечения колонны, стены, фундамента.
Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве – по её площади.
Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м 3 ] для объемной конструкции, в [H/м 2 ] — для площади, для линейной – в [H/м].
Продемонстрируем это на рисунке:
Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:
здесь AB является тяжестью, q – интенсивностью, которая измеряется в [H/м].
Примечательно, что сила приложена к середине данного отрезка AB.
На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:
где qmax – максимальная интенсивность [Н/м].
Q приложена к точке C, где AC равно: AC = 2/3 AB
Рассматривая функцию q(x), представленную на рисунке:
можно высчитать значение эквивалентной силы по формуле:
Равномерно и неравномерно распределенная нагрузка на балку
Единицы измерения распределённой нагрузки [Н/м].
Её также можно заменить на величину Q, которая приложена в середину AB.
Составим формулу: Q = q∗a
Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.
При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.
Пример решения задач с распределенной нагрузкой
Рассмотрим пример распределенной нагрузки на балку. Им может послужить тяга, благодаря которой происходит разрыв стальной стенки баллона с некоторым газом.
Для начала определяем результирующую давления в металлической трубе. Интенсивность равна q, радиус этого сектора трубы – R, ось симметрии Оx, а 2α – это центральный угол. Представим это на рисунке:
Выделим элемент сектора трубы ∆ϕ.
Затем определим единицу силы ∆Q. Она действует на плоскость дуги. Составим формулу:
Проекция результирующей тяги на ось Оx является:
Исходя из вышесказанного, можно найти проекцию этой же силы на ось Оy:
AB является хордой, которая стягивает дугу.
В нашей задаче сосуд – это ёмкость цилиндрической формы с высотой H, внутренним давлением P, действующим на стенки, и нагрузкой q = p [Н/м 2 ].
Разделим цилиндр вдоль его диаметра.
Исходя из этого, равнодействующая результирующих сил определяется по формуле:
где d – это внутренний диаметр цилиндра, h — его высота.
Формулу также можно записать следующим образом:
Итак, почему баллон имеет способность разрываться? На его стенки действуют значения S1, S2, S3 (площади), а также F, p (плотность), h (высота цилиндра) и R (его радиус). Рассчитаем их по формулам:
Изобразим баллон в момент разрыва:
Учтём a – толщину ёмкости. Таким образом напряжение, которое растягивает баллон, (усилия распространяются в том числе на крышку и дно цилиндра) равно:
Важную роль при решении практических задач также играет эпюра распределенной нагрузки – плоская фигура, которая ограничена графиком. Величина, действующая на балку, называется интенсивностью – силой, которая распространяется на единицы площади, объема или длины.
Лекция 7. Параллельные силы. Распределенная нагрузка
7.1. Сложение двух сонаправленных сил
Рассмотрим твердое тело, к точкам A1 и A2 которого приложены сонаправленные силы \(\vec F_<1>\) и \(\vec F_<2>\) (рис. 7.1 а). Если бы они были равны по модулю и перпендикулярны отрезку A1A2, то из соображений симметрии можно было бы заключить, что у них имеется равнодействующая \(\vec R\), приложенная в середине отрезка, сонаправленная с обеими силами и по модулю превосходящая каждую из них вдвое (рис. 7.1 б). Возникает вопрос: существует ли равнодействующая в общем случае, изображенном на рис. 7.1 а)?
Замечание. В нарушении симметрии роль играет лишь неравенство модулей сил, но не угол, образуемый векторами \(\vec F_<1>\), \(\vec F_<2>\) и отрезком A1A2. Например, силу \(\vec F_<2>\) можно перенести вдоль ее линии действия в некоторую точку B так, что новый отрезок A1B будет перпендикулярен этой силе.
Покажем, что и в общем случае у двух сонаправленных сил есть равнодействующая Для этого представим каждую из исходных сил \(\vec F_<1>\), \(\vec F_<2>\) в виде суммы двух новых сил: \(\vec F_<1>=\vec P_<1>+\vec Q_<1>\), \(\vec F_<2>=\vec P_<2>+\vec Q_<2>\). При этом потребуем, чтобы \(\vec P_<1>\) и \(\vec P_<2>\) были равны по модулю, противоположны по направлению и имели общую линию действия – A1A2 (рис. 7.2 а).
Рис. 7.2. Сложение двух сонаправленных сил
Согласно первой аксиоме статики, \(\vec P_<1>\) и \(\vec P_<2>\) уравновешивают друг друга. Поэтому исходная система \(\vec F_<1>,\vec F_<2>\) эквивалентна двум силам \(\vec Q_<1>,\vec Q_<2>\). Очевидно, что они непараллельны и лежат в той же плоскости, что и \(\vec F_<1>,\vec F_<2>\). Следовательно, их линии действия пересекаются в некоторой точке B этой же плоскости. Отложив силы \(\vec Q_<1>,\vec Q_<2>\) от этой точки и сложив по правилу параллелограмма, их можно заменить равнодействующей \(\vec R\).
Поскольку \(\vec P_<1>,\vec P_<2>\) уравновешивают друг друга, их также можно отложить от точки B. Это значит, что в B оказываются приложены силы \(\vec F_<1>=\vec P_<1>+\vec Q_<1>\) и \(\vec F_<2>=\vec P_<2>+\vec Q_<2>\). Поэтому равнодействующая \(\vec R\) равна \(\vec F_<1>+\vec F_<2>\): она сонаправлена с исходными силами, а по модулю равна их сумме.
Определим точку C, в которой линия действия \(\vec R\) пересекает отрезок A1A2. Треугольники, составленные из сил \(\vec F_<1>,\vec P_<1>,\vec Q_<1>\) и \(\vec F_<2>,\vec P_<2>,\vec Q_<2>\), подобны треугольникам BCA1 и BCA2, соответственно, поскольку их стороны параллельны (см. рис. 7.2 б). Поэтому
| $$\frac | (7.1) |
| $$F_<1>\cdot A_<1>C=F_<2>\cdot A_<2>C,\;\frac | (7.2) |
Найденную формулу можно сравнить с соотношением (5.2), выражающим правило рычага: чем больше сила F1, тем ближе к точке ее приложения должна находиться точка C. Такая аналогия не случайна. Действительно, если у сил \(\vec F_<1>,\vec F_<2>\) есть равнодействующая \(\vec R\), то имеется и уравновешивающая \(\vec R’\), которую можно считать приложенной в той же точке C (рис. 7.3).
Рис. 7.3. Аналогии с правилом рычага
Система \(\vec F_<1>,\vec F_<2>,\vec R’\) является уравновешенной. Из уравнений (4.3) следует, что сумма моментов этих сил относительно точки C равна нулю, т.е. F1d1 – F1d2 = 0. Но d1 = A1C cos α, d2 = A2C cos α, где α – угол между A1A2 и общим перпендикуляром к линиям действия сил \(\vec F_<1>,\vec F_<2>\). Поделив обе части равенства F1 d1 = F2 d2 на cos α, мы и придем к равенствам (7.2).
Точка C, таким образом, играет роль неподвижного шарнира, в котором следует закрепить рычаг A1A2, чтобы он оставался в равновесии под действием внешних сил \(\vec F_<1>,\vec F_<2>\). В качестве реакции шарнира надо рассматривать уравновешивающую \(\vec R’\).
Система из двух сонаправленных сил \(\vec F_<1>,\vec F_<2>\) имеет равнодействующую \(\vec R\), сонаправленную с ними. Ее модуль равен сумме исходных сил: R = F1 + F2, а положение ее линии действия между линиями действия исходных сил может быть определено по правилу рычага.
Найдем координаты точки C. Пусть A1 и A2 имеют радиус-векторы \(\vec r_<1>=\
| $$\vec r_ | (7.3) |
или, в координатной форме,
Замечание. Напомним, что точка C делит отрезок A1A2 в отношении λ, если она принадлежит прямой (не обязательно отрезку) A1A2 и \(\overrightarrow
С другой стороны, из уравнения (7.2) следует, что точка C делит отрезок A1A2 в отношении λ = F2/F1, считая от вершины A1. Подставляя это отношение в (7.3) и упрощая, получим окончательно:
| $$\vec r_ | (7.4) |
В частности, при F1 = F2 из (7.4) следует, что \(\vec r_
7.2. Сложение двух противоположно направленных сил
Рассуждая таким же образом, как и в предыдущем пункте, попробуем найти равнодействующую двух противоположно направленных сил \(\vec F_<1>\) и \(\vec F_<2>\). Без ограничения общности будем предполагать, что F1 ≤ F2. Все дополнительные построения и обозначения аналогичны тем, что введены на рис. 7.2.
Линии действия сил \(\vec Q_<1>,\vec Q_<2>\) по-прежнему пересекаются в точке B, что дает возможность отложить силы \(\vec F_<1>,\vec F_<2>\) от этой точки и найти их равнодействующую \(\vec R=\vec F_<1>+\vec F_<2>\) (рис. 7.4).
Рис. 7.4. Сложение двух противоположно направленных сил
За счет того, что \(\vec F_<1>\) и \(\vec F_<2>\) направлены противоположно, теперь модуль равнодействующей равен разности модулей исходных сил: R = F2 – F1. Вектор \(\vec R\) сонаправлен с \(\vec F_<2>\) (этот вектор имеет большую абсолютную величину).
При определении положения точки C можно по-прежнему использовать соотношение (7.1), но теперь эта точка находится вне отрезка A1A2 ближе к A2 (в этом конце отрезка приложена большая по модулю сила). Таким образом, теперь C делит отрезок A1A2 в отрицательном отношении λ = –F2/F1, считая от вершины A1. Подставив это значение в (7.3), найдем радиус-вектор точки приложения равнодействующей:
| $$\vec r_ | (7.5) |
Можно считать, что вместо (7.5) по-прежнему справедлива формула (7.4), если одну из величин F1 или F2 считать отрицательной, принимая во внимание противоположную направленность сил \(\vec F_<1>,\vec F_<2>\). При этом безразлично, какой именно величине, F1 или F1, приписать знак «–». В этом случае F1 и F1 будут уже не просто модулями \(\vec F_<1>,\vec F_<2>\), а проекциями сил на ось, сонаправленную с одним из векторов.
Итак, аналогично случаю двух сонаправленных сил, можно утверждать:
Система из двух не равных по величине противоположно направленных сил \(\vec F_<1>,\vec F_<2>\) имеет равнодействующую \(\vec R\), сонаправленную большей по модулю силой. Модуль равнодействующей равен модулю разности исходных сил: R = |F1 – F2|. Положение ее линии действия можно определить по правилу рычага, но она находится вне области, заключенной между линиями действия \(\vec F_<1>\) и \(\vec F_<2>\).
Оговорка о неравенстве сил по величине сделана не случайно, ее смысл поясняется ниже.
Выясним, что происходит с равнодействующей \(\vec R\) при различных соотношениях между F1 и F2. Если они равны по величине и знаку, то точка C, в которой приложена \(\vec R\), располагается в середине исходного отрезка A1A2, причем по модулю она будет в два раза больше, чем F1 или F2 (рис. 7.5 а).
Рис. 7.5. Равнодействующая при различных соотношениях между F1 и F2
Станем теперь уменьшать F1. Это приведет к тому, что будет уменьшаться и R, а точка C станет смещаться по направлению к A2 (рис. 7.5 б). При F1 = 0 мы получим, что R = F2, а из (7.4) следует, что в этом случае точки C и A2 совпадут. Впрочем, этот результат очевиден и без использования формул: фактически, при F1 = 0 на тело действует лишь сила F2. Если теперь поменять знак у F1 и тем самым «развернуть» \(\vec F_<1>\) в сторону, противоположную \(\vec F_<2>\), то C покинет отрезок A1A2 (рис. 7.5 в), а равнодействующая R окажется меньше, чем F2. При увеличении абсолютной величины F1 (с сохранением отрицательного знака) R продолжит уменьшаться, а C станет все больше и больше удаляться от A2.
Возникает вопрос: что произойдет при |F1| = |F2|, т.е. в случае, когда силы \(\vec F_<1>\) и \(\vec F_<2>\) образуют пару?
С одной стороны, величина равнодействующей (если таковая существует) станет равной нулю. С другой стороны, подставив F1 = –F2 в формулу (7.4) или F1 = F2 в (7.5), мы окажемся перед необходимостью делить на нуль. Следовательно, невозможно определить местоположение точки C – она «улетает» на бесконечность. Отсюда вытекает, что
Ранее этот факт уже упоминался без доказательства.
7.3. Сложение трех и более параллельных сил
Пользуясь результатами предыдущих пунктов, попытаемся найти равнодействующую нескольких (более двух) параллельных сил \(\vec F_<1>,\vec F_<2>,\ldots,\vec F_
Рис. 7.6. Система нескольких параллельных сил
Будем складывать силы попарно, аналогично тому, как ранее вычислялась равнодействующая сходящейся системы. В случае, когда сил всего три, рассуждения таковы. Сложив \(\vec F_<1>\) и \(\vec F_<2>\), найдем их равнодействующую \(\vec R_<1,2>\). Ее проекция на ось l равна сумме проекций \(\vec F_<1>\) и \(\vec F_<2>\), т.е. F1 + F2. Радиус-вектор \(\vec r_<1,2>\) точки приложения \(\vec R_<1,2>\) можно найти по формуле (7.4) с учетом знаков F1 и F2:
Итак, исходная система эквивалентна двум параллельным силам: \(\vec R_<1,2>\) и \(\vec F_<3>\), приложенным в точках с радиус-векторами \(\vec r_<1,2>\) и \(\vec r_<3>\), соответственно. Складывая их и упрощая выражения, найдем равнодействующую трех сил \(\vec R\), проекция которой на ось l составляет R = R1,2 + F3 = F1 + F2 + F3, а радиус-вектор точки приложения C равен
Аналогично, для произвольного количества n сил получим
\begin | (7.6) | |
В координатной форме второе равенство можно переписать так:
| $$x_ | (7.7) |
Конечно, знаменатель дроби в формулах для определения \(\vec r_
Пример. Параллельные силы \(\vec F_<1>,\vec F_<2>\) и \(\vec F_<3>\) имеют проекции 5 Н, –4 Н и 7 Н на направление вектора \(\vec F_<1>\) и приложены в точках A1(–1; 13; 6), A2(6; –3; 5) и A3(3; –3; 2), соответственно; все координаты даны в см. Найти равнодействующую этих сил и точку ее приложения.
Согласно первому из равенств (7.6), R = 5 – 4 + 7 = 8 Н. Тем самым, заданная система сил, действительно, имеет равнодействующую: R ≠ 0.
Вычислим координаты точки приложения найденной равнодействующей, используя (7.7):
xC = (–1·5 + 6·(–4) + 3·7)/8 = –1 см, yC = (13·5 – 3·(–4) – 3·7)/8 = 7 см, zC = (6·5 + 5·(–4) + 2·7)/8 = 3 см.
Соотношения (7.6) и (7.7) справедливы, если сумма проекций всех параллельных сил на одну и ту же ось l отлична от нуля. В противном случае система приводится не к равнодействующей, а к паре, аналогично п. 7.2.
Как следует из второй аксиомы статики, равнодействующая системы параллельных сил – скользящий вектор. Поэтому ее необязательно прикладывать в точке C, определяемой из формул (7.6). Достаточно выбрать любую точку на прямой, проходящей через C и имеющей \(\vec R\) в качестве направляющего вектора. Поэтому, используя указанное выше соотношение, мы накладываем на точку приложения равнодействующей дополнительное ограничение.
Зато появляется другая «свобода маневра». Ось l проводится не произвольно, а «привязывается» к самим параллельным силам. Соответственно, величины F1, F2. Fn описывают лишь ориентацию этих сил относительно друг друга. Если все векторы \(\vec F_<1>,\vec F_<2>,\ldots,\vec F_
Рис. 7.7. Поворот системы параллельных сил
Если система параллельных сил имеет равнодействующую, то ее величина и точка приложения не меняются при одновременном повороте всех сил на один и тот же угол и не зависят от ориентации сил относительно неподвижной системы координат.
Такая точка C, что при любом одновременном повороте системы параллельных сил линия действия ее равнодействующей проходит через C, называется центром параллельных сил. Из вышесказанного следует, что координаты этого центра могут быть вычислены по формуле (7.6), если, конечно, существует сама равнодействующая.
В частности, если силы \(\vec F_<1>,\vec F_<2>,\ldots,\vec F_
7.4. Распределенная нагрузка
Как уже было сказано в п. 1.1, силу (нагрузку) называют распределенной, если она приложена ко всем точкам некоторой линии, поверхности или объема. При проектировании различных механизмов, зданий и сооружений учет распределенных сил играет очень важную и даже решающую роль.
Пример 1. Одной из деталей двигателя внутреннего сгорания является поршень, размещаемый внутри цилиндра (рис. 7.8). При сгорании рабочая смесь воздуха и распыленного топлива в цилиндре расширяется и давит на поршень, толкая его. Это усилие передается на коленчатый вал, а от него – на оси колес автомобиля, что и заставляет их вращаться. Сила давления сгорающей смеси на поршень распределяется по площади его головки.
Рис. 7.8. Поршень с шатуном
Пример 2. Выпадающий снег может создавать значительное давление на крышу здания (рис. 7.9 а). Если эту снеговую нагрузку не учитывать, крыша может не выдержать и обрушиться (рис. 7.9 б).
Рис. 7.9. Снеговая нагрузка на крышу здания
Основная характеристика распределенной нагрузки – ее интенсивность (плотность, удельная нагрузка): сила, приходящаяся на единицу длины, площади или объема. Первые две величины называют также погонной нагрузкой и давлением, соответственно. В системе СИ интенсивность нагрузки измеряют в Н/м, Н/м 2 (паскалях – Па) и Н/м 3 в зависимости от того, распределена сила по длине, площади или объему.
Так, если давление p на участке поверхности площади S постоянно, то для вычисления суммарной силы F, действующей на этот участок, нужно умножить его площадь на давление: F = pS. После этого останется учесть направление приложенной силы (рис. 7.10).
Чтобы найти силу, действующую на всю поверхность (объем, длину), можно было бы умножить интенсивность нагрузки на общую площадь поверхности. Однако трудность заключается в том, что интенсивность распределенной нагрузки может быть не постоянной,а изменяться от точки к точке как по величине, так и по направлению.
Пример 1. При ходьбе босиком по песку пятка и пальцы оставляют более четкий след, чем остальная часть ступни (рис. 7.11). Это значит, что интенсивность нагрузки (в роли которой выступает вес человека), приходящейся на пальцы и пятку, выше.
Рис. 7.11. След на песке показывает, что вес человека распределен по его ступням неравномерно
Пример 2. Значительное влияние на устойчивость зданий и сооружений (особенно тех, что имеют большие размеры), оказывает ветровая нагрузка. Давление, создаваемое подвижными воздушными массами, изменяется от точки к точке и зависит от многих факторов: температуры, влажности и т.д. Ветровая нагрузка на сооружения может расчитываться с помощью ЭВМ. Кроме того, для моделирования такой нагрузки макеты сооружений могут обдуваться в аэродинамической трубе, подобно летательным аппаратам.
Часто можно предположить, что силы, приложенные во всех точках изучаемого объема (поверхности, линии) параллельны друг другу. Тогда можно попытаться найти их равнодействующую, пользуясь формулами (7.6).
Мы рассмотрим лишь простейшую ситуацию: силу, распределенную по прямолинейному отрезку. Будем предполагать, что силы, приложенные в разных точках, параллельны друг другу и перпендикулярны рассматриваемому отрезку. В этом случае наглядно представить интенсивность нагрузки можно с помощью специального графика – эпюры напряжений (рис. 7.12).
Рис. 7.12. Эпюра напряжений
Пусть нагрузка распределена по отрезку [a; b] оси Ox. Тогда величина погонной нагрузки p(x) в каждой конкретной точке зависит от координаты x этой точки. График функции p(x) и является искомой эпюрой.
Если выбрать на исходном отрезке [a; b] настолько мелкий участок Δx, что интенсивность нагрузки на его протяжении практически не успевает измениться, то суммарная сила ΔF, приложенная к этому участку, будет приближенно равна p(x)Δx (см. рис. 7.12). Значит, чтобы вычислить силу F, приложенную ко всему отрезку [a; b], надо разбить его на мелкие участки dx1, dx2. dxn, внутри каждого из них выбрать точку (x1, x2. xn, соответственно), приближенно вычислить силу, приложенную к этим участкам, а результаты сложить:
Действительно, силы, приложенные к разным участкам разбиения, параллельны друг другу (при введенных выше ограничениях), а значит, можно попытаться найти их равнодействующую по формуле (7.6). Чтобы определить координату точки приложения равнодействующей, используем равенство (7.7):
| $$x_ | (7.8 б) |
причем F вычисляется по формуле (7.8 а).
Конечно, результат вычислений в (7.8 а) и (7.8 б) будет тем точнее, чем мельче разбиение отрезка. В пределе, когда длины всех участков dx1, dx2. dxn стремятся к нулю (а их количество, соответственно, к бесконечности), сумма (7.8 а) переходит в определенный интеграл, а выражение для xC – в отношение двух интегралов:
Тем самым, суммарная нагрузка, приложенная к отрезку, представляет собой площадь криволинейной трапеции под графиком функции p(x).
Пример. Нагрузка распределена по отрезку [1; 4] с интенсивностью p(x) = –x 2 + 4x. Найти равнодействующую распределенных сил, приложенных к отрезку, и точку ее приложения.
Как и следовало ожидать для случая сонаправленных сил, точка приложения равнодействующей оказывается внутри отрезка: 1 ≤ 9/4 ≤ 4. Отметим, что p(1) = 3, p(4) = 0, так что правый конец отрезка не нагружен (рис. 7.13).
В наиболее простых случаях нагрузка распределяется по отрезку равномерно или линейно.
При равномерном распределении плотность p постоянна (рис. 7.14). В этом случае сосредоточенная равнодействующая равна произведению плотности на длину отрезка и прикладывается к его середине: F = p·(b–a), xC = (a + b)/2.
Рис. 7.14. Равномерно распределенная нагрузка
Пример. Нагрузку, создаваемую железнодородным составом на рельсы, можно считать равномерно распределенной: на каждый метр железнодорожного полотна, находящийся под составом, приходится примерно равный вес груза.
При линейном распределении погонная нагрузка возрастает от 0 на одном конце отрезка до некоторого значения pmax на другом конце; значения нагрузки в промежуточных точках пропорциональны расстоянию до ненагруженного конца. Для простоты рассмотрим отрезок [0; l] и предположим, что его левый конец свободен от нагрузки (рис. 7.15).
Рис. 7.15. Линейно распределенная нагрузка
Тогда получим p(0) = 0, p(l) = pmax, p(x) = pmax x/l. Подставив a = 0, b = l, а также найденное выражение для p(x) в (7.9), найдем F = lpmax/2, xC = 2l/3. Как и следовало ожидать, суммарная нагрузка равна площади прямоугольного треугольника с катетами pmax и l – именно такую фигуру ограничивает эпюра напряжений. Равнодействующая прикладывается на расстоянии, равном 2/3 длины отрезка, считая от ненагруженного конца.
Пример. Рассмотрим сваю, вертикально вбитую в дно водоема и испытывающую давление со стороны воды (согласно закону Паскаля, давление в жидкости не зависит от направления прилагаемого усилия, поэтому нельзя считать, что давление осуществляется только на горизонтальное дно водоема). Как известно из курса физики, указанное давление равно p = ρgz, где ρ – плотность жидкости, g – ускорение свободного падения, z – глубина, отсчитанная от свободной поверхности жидкости. Тем самым, интенсивность распределенной нагрузки линейно зависит от глубины z. Поэтому при замене распределенной нагрузки на сосредоточенную следует прикладывать равнодействующую на глубине, равной 2/3 глубины водоема (рис. 7.16).
Если силы, распределенные по объему (поверхности, линии) не параллельны, то можно по отдельности найти сосредоточенные равнодействующие \(\vec R_
Пример. Как уже говорилось, при жесткой заделке реактивная нагрузка распределяется по некоторой площади. При замене этой распределенной нагрузки на сосредоточенную возникает не только сила, но и реактивный момент.
Вопросы для самоконтроля
Задачи к лекции
Горизонтальная балка AE длины 7 м находится под действием сосредоточенной силы \(\vec F\), приложенной в точке D, находящейся на расстоянии 1 м от точки E, а также нагрузки, распределенной по отрезкам AB = 2 м и BC = 3 м. Отрезок AB нагружен равномерно с интенсивностью pmax = 100 кН/м, отрезок BC – линейно (рис. 7.17). Величина силы \(\vec F\) составляет 50 кН. Определить реакции жесткой заделки в точке A. Найти координату точки приложения сосредоточенной равнодействующей всех перечисленных сил (за исключением реакции заделки). Весом балки пренебречь.
Ответы. 1. A4(7; 1; 9). 2. XA = 0, YA = 300 кН, mA = 350 кН·м, x = 7/6 м. 3. Да.
Также рекомендуется решить задачи из §§3,4 [2]; РГР С1 [3].