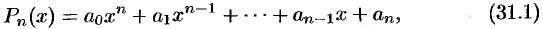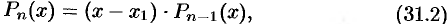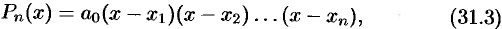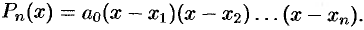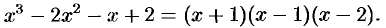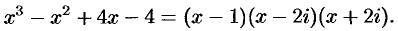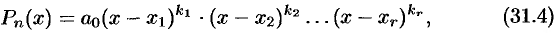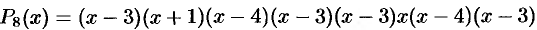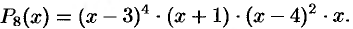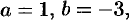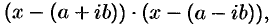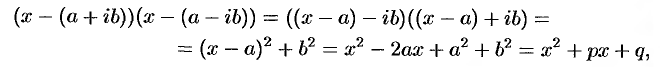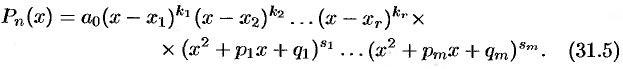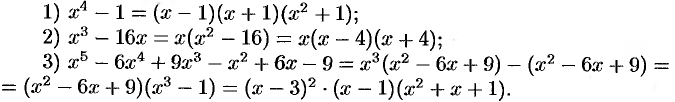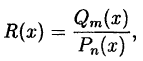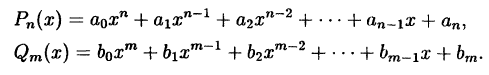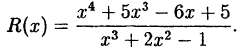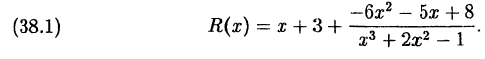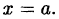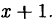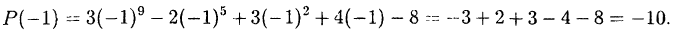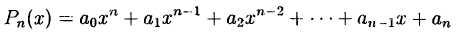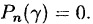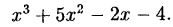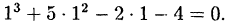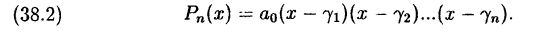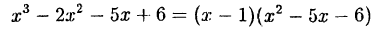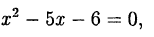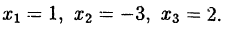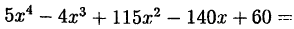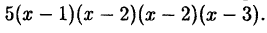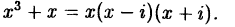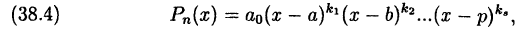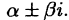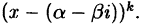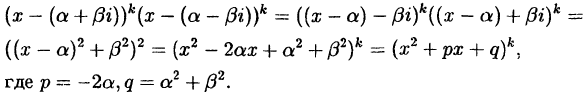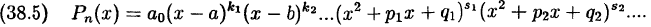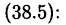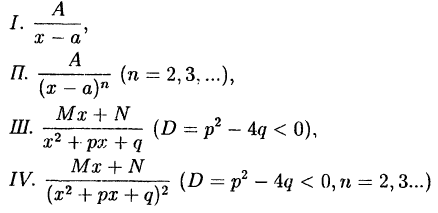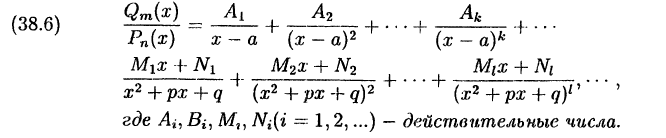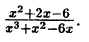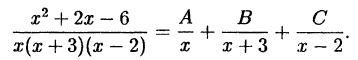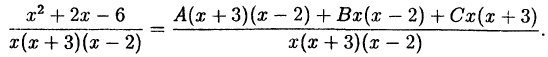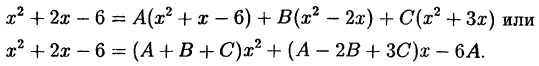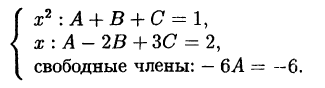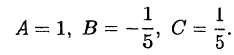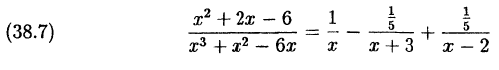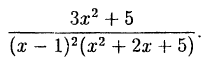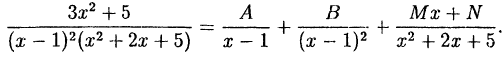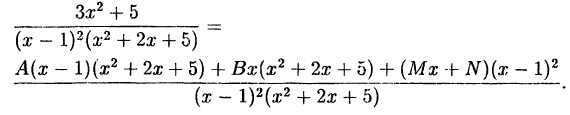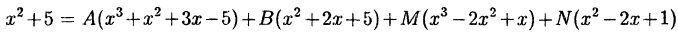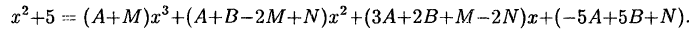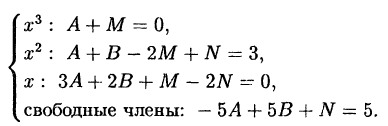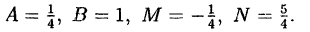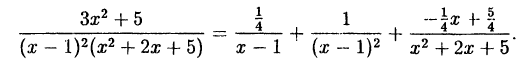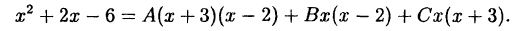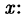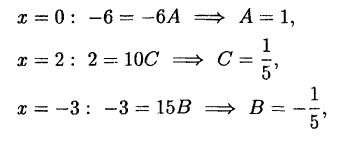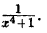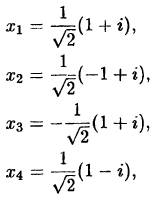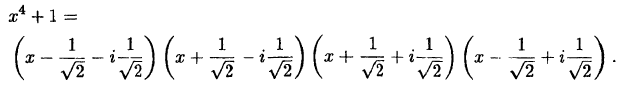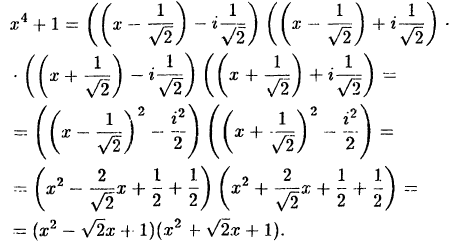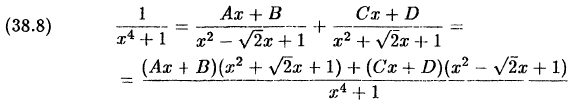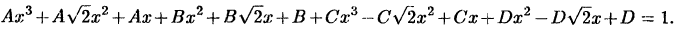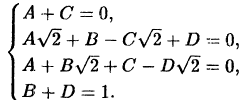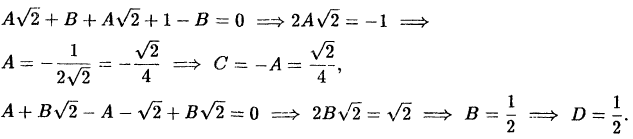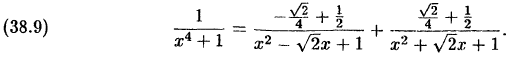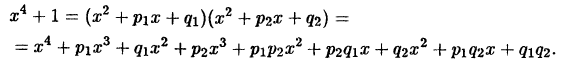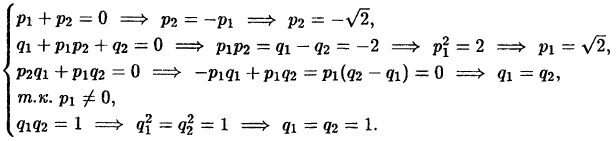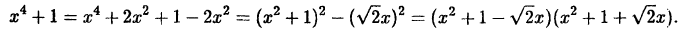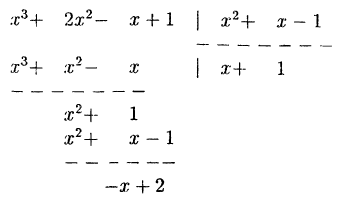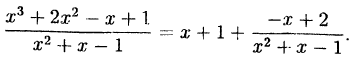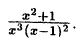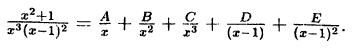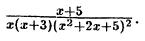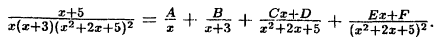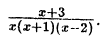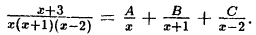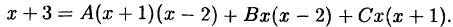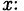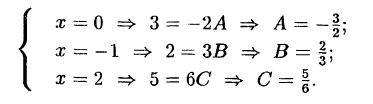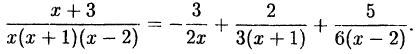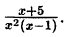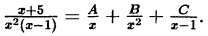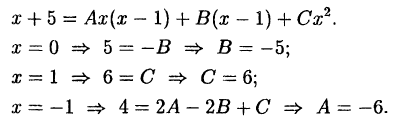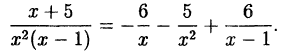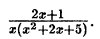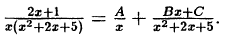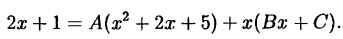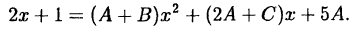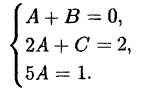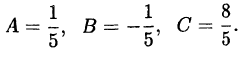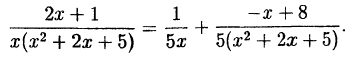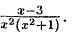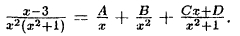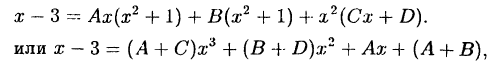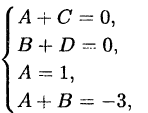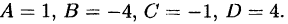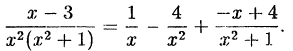что такое рациональная функция
Рациональная функция
Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид
где 

Частным случаем являются рациональные функции одного переменного:

Другим частным случаем является отношение двух линейных функций — дробно-линейная функция.
Свойства
Правильные дроби
Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.
Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби
Любую рациональную дробь многочленов с вещественными коэффициентами можно представить как сумму рациональных дробей, знаменателями которых являются выражения 


См. также
Полезное
Смотреть что такое «Рациональная функция» в других словарях:
РАЦИОНАЛЬНАЯ ФУНКЦИЯ — функция, получающаяся в результате конечного числа арифметических операций (сложения, умножения и деления) над переменным x и произвольными числами; имеет вид: R(x) = P(x)Q(x), где P(x) и Q(x) многочлены от x … Большой Энциклопедический словарь
рациональная функция — функция, получающаяся в результате конечного числа арифметических операций (сложения, умножения и деления) над переменным х и произвольными числами; имеет вид: R(х) = Р(х)/Q(х), где P(х) и Q(х) многочлены от х. * * * РАЦИОНАЛЬНАЯ ФУНКЦИЯ… … Энциклопедический словарь
РАЦИОНАЛЬНАЯ ФУНКЦИЯ — функция, получающаяся в результате конечного числа ариф метич. операций (сложения, умножения и деления) над переменным х и произвольными числами; имеет вид: R(x) = P(x)/Q(x), где Р(х) и Q(x) многочлены от х … Естествознание. Энциклопедический словарь
РАЦИОНАЛЬНАЯ ФУНКЦИЯ — 1) Р. ф. функция w=R(z), где R(z) рациональное выражение от z, т. е. выражение, полученное из независимого переменного z и нек рого конечного набора чисел (действительных или комплексных) посредством конечного числа арифметич. действий. Р. ф.… … Математическая энциклопедия
ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ — см. Рациональная функция … Математическая энциклопедия
Целая рациональная функция — алгебраический многочлен, т. е. функция вида w = a0 + a1z + a2z2 +. + anzn. См. Многочлен … Большая советская энциклопедия
Рациональная интерполяция — (интерполяция рациональными функциями) представление интерполируемой функции (точнее говоря, ряда табличных значений) в виде отношения двух полиномов. Ряд функций, плохо интерполируемых полиномиальными методами, удаётся хорошо приблизить… … Википедия
Рациональная дробь — Рациональная дробь это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид где P(x) и Q(x) некоторые многочлены. Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями.… … Википедия
Математика
This wiki’s URL has been migrated to the primary fandom.com domain.Read more here
Рациональная функция
Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид
где 

Частным случаем являются рациональные функции одного переменного:

Другим частным случаем является отношение двух линейных функций — дробно-линейная функция.
Свойства
Правильные дроби
Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби
Любую рациональную дробь многочленов с вещественными коэффициентами можно представить как сумму рациональных дробей, знаменателями которых являются выражения 


Рациональная функция с примерами решения и образцами выполнения
Многочлен (некоторые сведения справочного характера):
где 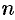
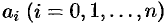
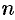
Корнем многочлена (31.1) называется такое значение 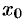
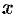
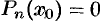
Теорема:
Если 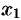
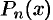
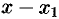
где 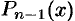

Возникает вопрос: всякий ли многочлен имеет корень? Положительный ответ на этот вопрос дает следующее утверждение.
Теорема:
Основная теорема алгебры. Всякий многочлен 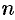
Доказательство этой теоремы мы не приводим.
Пользуясь основной теоремой алгебры, докажем теорему о разложении многочлена на линейные множители.
Теорема:
Всякий многочлен 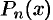
где 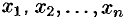
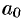
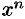
Рассмотрим многочлен (31.1). По теореме 31.2 он имеет корень. Обозначим его через 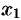
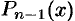
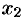
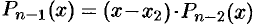
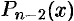
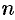
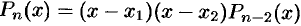
Продолжая этот процесс, получим в итоге:
Множители 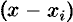
Пример:
Разложить многочлен 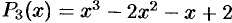
Решение:
Многочлен 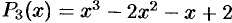
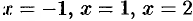
Пример:
Представить выражение 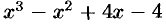
Решение:
Легко проверить, что
Если в разложении многочлена (31.3) какой-либо корень встретился 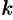
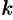
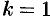
Разложение многочлена (31.3) можно записать в виде
если корень 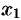
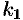
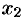
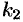

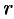
можно записать так:
Пользуясь теоремой 31.3, можно доказать следующие утверждения.
Теорема:
Если многочлен 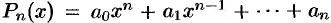
Теорема:
Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Например, если 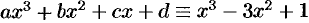
Теорема:
Если многочлен 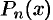
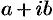
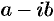
В разложении многочлена (31.3) комплексные корни входят сопряженными парами. Перемножив линейные множители
получим трехчлен второй степени с действительными коэффициентами 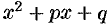
где 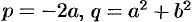
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами.
С учетом вышеизложенного справедлив следующий факт.
Теорема:
Всякий многочлен с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами, т. е. многочлен 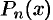
При этом 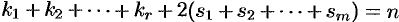
Примеры разложений (31.5):
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
Рациональная функция одной переменной
Рациональной функцией или рациональной дробью называется функция, равная частному от деления двух многочленов:
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя и неправильной — в противном случае. Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной дроби.
Пример:
Представить в виде суммы многочлена и правильной
дроби следующую неправильную дробь:
Решение:
Разделив числитель на знаменатель получим в частном 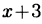
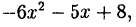
Остаток от деления многочлена 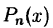
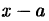
Теорема Везу:
Остаток от деления многочлена 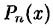
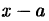
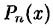
Пример:
Найти остаток от деления многочлена 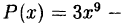
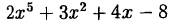
Решение:
Здесь 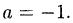
Некоторые сведения о многочленах
Рассмотрим кратко
некоторые сведения о многочленах, которые понадобятся нам в
дальнейшем.
называется всякое число 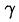
Пример:
Проверить, что 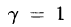
Решение: Действительно:
2. Имеет место следующая теорема, принимаемая без доказательства:
Теорема:
Всякий многочлен степени 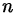
представлен в виде произведения 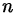

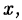
Числа 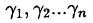
Если в разложении 38.2 раскрыть скобки, то свободный член
многочлена будет равен произведению корней многочлена
Отсюда вытекает следующее правило: Если многочлен 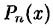
целые корни, то эти корни являются делителями свободного члена.
Так как любое число имеет конечное множество целых делителей, то
это правило позволяет решать алгебраические уравнения степени выше двух при условии, что хотя бы один корень — целое число.
Пример:
Решение:
Если у него есть целые корни, то только 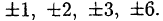
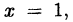
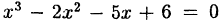
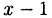
Решив квадратное уравнение
Пример:
Легко проверить, что
Пример:
Многочлен
3. Среди линейных множителей в (38.2) могут быть одинаковые.
Объединяя их, можем записать разложение многочлена на множители в виде:
где все корни 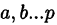
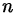
Корни 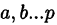
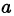
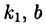
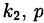
4. Среди корней в разложении (38.2) могут быть комплексное
В алгебре доказывается: если 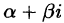
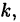
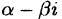
5. Поэтому, если в разложении (38.4) есть множитель 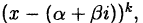
Перемножив два множителя, соответствующие комплексным
сопряженным корням, получим (см. 37.7):
Обратите внимание что трехчлен 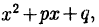
квадратов имеет отрицательный дискриминант.
6. Все вышесказанное позволяет сформулировать утверждение:
всякий многочлен с действительными коэффициентами можно представить в следующем виде:
В
В нем линейные множители соответствуют действительным корням,
а квадратные трехчлены, имеющие по два корня — комплексным корням многочлена.
Разложение правильной рациональной дроби на простейшие
Определение:
называются простейшими дробями первого, второго, третьего и
четвертого типов.
В высшей алгебре доказывается следующая теорема, которую мы
принимаем без доказательства:
Теорема:
Правильную рациональную дробь 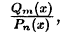
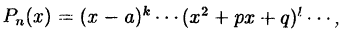
разложить на сумму простейших дробей:
В формуле (38.6) первое многоточие в разложении многочлена 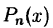
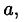
Из формулы (38.6) следует, что линейным множителям в разложении знаменателя соответствуют дроби I и II типов, а квадратичным множителям соответствуют простейшие дроби III и IV типов.
При этом число простейших дробей, соответствующих данному
множителю, равно степени, с которой этот множитель входит в разложение знаменателя дроби на множители.
Правило разложения правильной рациональной дроби остается
справедливым при любом числе линейных и квадратичных множителей в разложении знаменателя
Рассмотрим два способа нахождения коэффициентов разложения (38.6).
Метод неопределенных коэффициентов
Этот метод основан
на следующем утверждении, принимаемом без доказательства: если два многочлена тождественно равны, то равны и коэффициенты при
одинаковых степенях неизвестной в обеих частях тождества.
Поэтому приводя в правой части разложения (38.6) к общему
знаменателю, получаем тождественное равенство двух рациональных дробей с равными знаменателями.
Следовательно, числители тождественно равны. Приравнивая
коэффициенты при одинаковых степенях неизвестной, получим систему линейных уравнений, относительно неизвестных коэффициентов 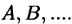
Пример:
Разложить на простейшие дроби:
Решение:
Приводим правую часть этого тождества к общему знаменателю:
Приравниваем коэффициенты при одинаковых степенях
Можно показать, что эта система всегда имеет единственное решение.
Это решение следующее:
Подставив найденные коэффициенты в разложение (38.7),
окончательно получим:
Пример:
Разложить на простейшие дроби:
Решение:
Приведем правую часть к общему знаменателю:
Приравнивая числители, получаем:
Приравнивая коэффициенты при одинаковых степенях ж получаем
систему:
Ее решение:
Следовательно, подставив найденные коэффициенты в (38.8), получим:
Метод произвольных значений
Этот метод основан на
утверждении: если два многочлена тождественно 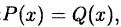
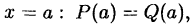
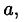
Поэтому вместо приравнивания коэффициентов при одинаковых
степенях неизвестной в разложении (38.6) можно подставлять туда вместо 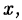
Этот метод особенно эффективен когда многочлен 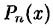
знаменателе имеет различные действительные корни и в качестве
произвольных значений берутся числа, равные действительным корням знаменателя.
Пример:
Разложить на простейшие дроби функцию из примера (38.7).
Решение:
Ранее, при использовании метода неопределенных
коэффициентов было получено:
Подставим в это тождество последовательно три значения
Опять получаем соотношение (38.7).
Рассмотрим теперь пример, в котором для разложения знаменателя на множители можно использовать операцию извлечения корня из комплексного числа.
Пример:
Разложить на простейшие дроби
Решение:
Многочлен 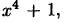
комплексные корни, которые мы нашли в лекции 37:
Объединив первую скобку с последней, вторую с третьей, получим:
В соответствии с формулой (38.6) и методом неопределенных
коэффициентов, находим:
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях равенства, получим систему уравнений для определения неизвестных
Выразив из первого уравнения С через А, а из последнего D через В и подставив 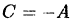
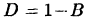
Подставляя найденные значения 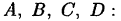
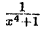
Замечание:
Разложение (38.9) многочлена 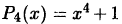
множители можно было бы получить и методом неопределенных коэффициентов.
Учитывая, что комплексные корни входят в разложение многочлена на множители как корни квадратных трехчленов вида 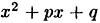
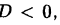
Приравнивая коэффициенты при одинаковых степенях 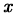
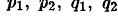
Отметим, что 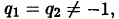
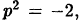
Замечание:
Разложить 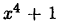
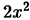
Этот пример показывает, что нестандартные приемы решения часто очень эффективны!
Разложение рациональных дробей на простейшие
Рассмотрим прежде всего примеры на выделение целой части в
неправильной дроби.
Пример:
Представить неправильную дробь 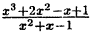
Решение:
Разделим числитель на знаменатель
В следующих примерах представим (без отыскания коэффициентов)
правильную дробь в виде суммы элементарных дробей.
Пример:
Решение:
Пример:
Решение:
В следующих примерах разложить правильную дробь на простейшие и найти коэффициенты разложения с помощью метода произвольных значений.
Пример:
Решение:
В правой части тождества приводим к общему знаменателю и
приравниваем числители:
Подставляем в обе части тождества произвольные значения
Пример:
Решение:
В следующих примерах разложить правильную дробь на простейшие и найти коэффициенты с помощью метода неопределенных коэффициентов.
Пример:
Решение:
Приведем в правой части к общему знаменателю и приравняем
числители
Раскроем скобки и приведем подобные члены
Приравняем коэффициенты при одинаковых степенях
Решив эту систему, найдем
Пример:
Решение:
откуда
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института