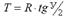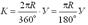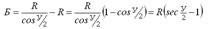что такое радиус кривой в геодезии
РАДИУС КРИВОЙ
расстояние от центра кривой до оси пути. От размеров Р. к. зависит кривизна данного участка жел.-дор. пути: чем больше Р. к., тем меньше кривизна, тем меньше сопротивление движению поезда в пределах кривой и тем меньше износ рельсов и колесных пар подвижного состава. При проектировании ж. д. в кривых участках пути стремятся поэтому применять большие радиусы (2 000 — 1 000 м); однако в трудных топографических условиях (напр. в гористой местности) это не всегда выполнимо и может вызывать значительное увеличение объема земляных работ и удорожание строительства. В связи с этим ТУ проектирования ж. д. разрешается в отдельных трудных местах уменьшать размеры Р. к. до 300 м. В случаях необходимости расположения станций, разъездов и обгонных пунктов на кривых радиус их д. б. не менее 600 м, а в горных условиях — 500 м (ПТЭ, § 11).
Смотреть что такое «РАДИУС КРИВОЙ» в других словарях:
Радиус кривой в плане наименьший — радиус, при котором обеспечивается безопасное движение автомобилей с расчетной скоростью при чистом увлажненном покрытии, с устройством виражей и уширением проезжей части. Источник: Справочник дорожных терминов … Строительный словарь
РАДИУС — (лат. radius луч). 1) полупоперечник круга; в кривых линиях и кривых поверхностях линия, проведенная от центра в окружности. 2) кость, лежащая рядом с локтевою и образующая с нею локтевую часть руки. Радиус вектор. Расстояние какой нибудь точки… … Словарь иностранных слов русского языка
Радиус — окружности У этого термина существуют и другие значения, см. Радиус (значения). Радиус (лат. … Википедия
радиус кривизны переходной кривой зуба в точке — (ρf) радиус кривизны переходной кривой [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины понятия, относящиеся к зубчатому колесупрофиль зуба Синонимы радиус кривизны переходной кривой … Справочник технического переводчика
РАДИУС-ВЕКТОР — термин, которым в конических сечениях (эллипсе, гиперболе, параболе) называется расстояние какой нибудь точки кривой линии от её фокуса. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. радиус вектор 1) мат. а)… … Словарь иностранных слов русского языка
радиус поворота планировщика полей — радиус поворота Радиус минимальной окружности, в которую вписывается тягач с планировщиком полей при движении по кривой. [ГОСТ 22313 77] Тематики машины и орудия для обработки почвы Синонимы радиус поворота … Справочник технического переводчика
радиус кривизны переходной кривой исходного контура в граничной точке профиля зуба — (ρf) [ГОСТ 19325 73] Тематики передачи зубчатые конические Обобщающие термины исходные контуры и производящие поверхности конических зубчатых колес … Справочник технического переводчика
Радиус кривизны — радиус круга кривизны (См. Кривизна) в данной точке кривой … Большая советская энциклопедия
радиус кривизны — 2.8 радиус кривизны: Радиус дуги окружности, наиболее точно соответствующей форме закругления рассматриваемого элемента. Источник … Словарь-справочник терминов нормативно-технической документации
Основные элементы круговой кривой. Расчет



На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего транспортного средства устраивают закругления или кривые. Закругления могут быть любыми. Простейшим является дуга окружности определенного радиуса, т.е. круговая кривая.
На железнодорожных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 400 и 300 м. Конкретное решение о применении радиусов железнодорожных кривых принимают в соответствии с конкретными условиями и строительно-техническими нормами СТН Ц-01-95.
Круговая кривая характеризуется четырьмя главными точками и шестью основными элементами (рис. 83).
Главными точками кривой, которые определяют положение кривой на местности, являются: вершина угла ВУ; начало круговой кривой НКК; середина круговой кривой СКК; конец круговой кривой ККК.
Основными элементами кривой являются:
1. Угол поворота трассы У.
2. Радиус закругления R.
Во время изысканий угол У вычисляют, а радиус R назначают. Остальные элементы находят по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НКК, О (рис. 83).
3. Тангенс кривой (касательная) Т – расстояние по прямой от вершины угла до начала или конца кривой.
4. Длина кривой К от начала кривой до её конца.
5. Биссектриса кривой Б – отрезок от вершины угла до середины кривой.
6. Домер Д – разность между длиной двух тангенсов и кривой.
Все элементы кривой можно вычислить по вышеприведенным формулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла поворота и радиуса, то для их определения составлены специальные таблицы для разбивки кривых.
Вычислить пикетажные значения главных точек кривой – значит узнать на каких пикетах и плюсовых точках они находятся.
Сначала определяют пикетаж вершины угла поворота ВУ, а затем находят пикетажное значение начала, конца и середины кривой
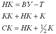
Расчет радиуса круговой кривой по стрелам изгиба — геодезия
Радиус круговой кривой может быть выражен через стрелу изгиба по общеизвестной формуле:
т.е. величину стрелы изгиба можно рассматривать как кривизну, выраженную в определенном масштабе.
Положение в плане точек деления существующей кривой, а также проектной кривой относительно касательной АВ может быть установлено по величине отрезков 1—2, 2—5, 3—4 и т.д., равных ΔK, и углам поворота этих отрезков α1, α2, α3 и т.д.
Выражая в последней формуле величины углов поворота через стрелы изгиба согласно равенствам (III.22), в результате чего ΔK сократится, получим следующие формулы для длины эвольвенты:
Таким образом, длина эвольвенты какой-либо точки деления кривой равна согласно первому выражению удвоенной сумме сумм всех предыдущих стрел изгиба, измеренных в точках деления кривой, и равна также согласно второму выражению удвоенной сумме статических моментов всех предыдущих стрел изгиба относительно этой точки.
Если сумму статических моментов стрел выразить через момент суммы стрел (через момент равнодействующей), то длина эвольвенты будет равна:
Круговые и переходные кривые.
Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).
Рис. 15.3 Схема круговой кривой
Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:
Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):
Домер вычисляют по формуле

Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.
В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:
Правильность вычислений контролируют по формулам:
Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.
По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.
Вычислим пикетажное положение главных точек:
ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00
ПК НК 5 + 39,27 7 + 32,73
ПК КК 7 + 31,08 ПК КК 7 + 31,08
ПК НК 5 + 39,27 ПК ВУ 6 + 36,00
ПК СК 6 + 35,17 ПК СК 6 + 35,18
Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой 

R – радиус кривизны в конце переходной кривой.
Индексом k отмечены значения переменных в конце переходной кривой.
Для радиуса кривизны переходной кривой в текущей точке i найдём:
где через l обозначена длина переходной кривой sk. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.
Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол

Подставляя выражение радиуса кривизны r из (15.5), получим

Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:

Рис. 15.4 Схема переходной кривой:
а – углы поворота трассы: φ – в текущей точке i, β – в конце
Из полученного уравнения вытекают формулы:


Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):
Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):
Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:




Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:

Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.
Рис. 15. 5 Смещение начала переходной кривой
Рис. 15.6 Сопряжение круговой кривой
Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q1 и имеющая длину K = Ra.
При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна
Тангенс и биссектриса определяются по формулам:
Домер в этом случае равен

В полевых условиях значения m, Тp и Бp вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).
Круговая кривая
Круговая кривая — дуга круга, служащая для плавного сопряжения в горизонтальной плоскости двух смежных прямых участков железнодорожного пути. Круговая кривая соединяется с прямым участком при помощи переходных кривых. Круговые кривые применяют на участках обхода препятствий и развития трассы с целью уменьшения объёмов земляных работ и стоимости строительства искусственных водопропускных сооружений. По сравнению с прямыми участками круговая кривая обладает недостатками (снижение скорости движения поездов, уменьшение сцепления ведущих колёс локомотива с рельсами, увеличение износа колёс подвижного состава и расходов по текущему содержанию и ремонту пути, необходимость усиления конструкции верхнего строения пути).
Круговая кривая характеризуется углом поворота, радиусом и положением вершины угла. На практике для определения элементов круговой кривой и её разбивки применяют специальные таблицы.
Кривые участки пути новых железных дорог следует проектировать возможно больших радиусов. Радиусы кривых следует назначать в соответствии с таблицей 1 и принимать равными, м: 4000, 3000, 2500, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 500, 400, 350, 300, 250, 200.
Величину наименьшего радиуса кривых при проектировании дополнительных главных путей и усиления (реконструкции) существующих железных дорог следует устанавливать в зависимости от намечаемых скоростей движения пассажирских и грузовых поездов и величины радиусов кривых существующего пути.
| Категории железнодорожной линии | Радиусы кривых в плане, м | |||
|---|---|---|---|---|
| рекомендуемые | допускаемые | |||
| в трудных условиях | в особо трудных условиях | по согласованию | ||
| Скоростные | 4000 – 3000 | 2500 | 1200 | 800 |
| Особогрузонапряжённые | 4000 – 2000 | 1500 | 1000 | 600 |
| I | 4000 – 2500 | 2000 | 1000 | 600 |
| II | 4000 – 2000 | 1500 | 800 | 400 |
| III | 4000 – 1200 | 800 | 600 | 350 |
| IV (железнодорожные линии) | 2000 – 1000 | 600 | 350 | 200 |
| IV (подъездные пути) | 2000 – 600 | 500 | 200 | 200 |
| IV (соединительные пути) | 2000 – 350 | 250 | 200 | 200 |
1. В случаях, когда на особогрузонапряженных линиях предусматривается максимальная скорость движения пассажирских поездов свыше 120 км/ч, радиусы кривых, рекомендуемые и допускаемые в трудных условиях, на указанных линиях следует принимать по нормам, предусмотренным для линий I категории.
2. При проектировании участков железнодорожных линий на пересечении высотных препятствий, где по условиям продольного профиля пути реализуются скорости движения пассажирских поездов менее 120 км/ч и грузовых поездов менее 60 км/ч по согласованию с владельцем инфраструктуры допускается применять кривые радиусами: 300 м — на линиях I и II категории, 250 м — на линиях III категории.
3. При проектировании уширений междупутий допускается применять кривые радиусом более 4000 м.
4. При проектировании развязок в железнодорожных узлах допускается применять кривые радиусом 250 м.
Кривые участки дополнительных главных путей, располагаемые на общем земляном полотне с существующим путем, следует проектировать концентричными по отношению к выправленным кривым существующего пути.
При переустройстве кривых существующего пути следует принимать постоянные значения радиусов на всем протяжении круговой кривой. В трудных условиях, когда выполнение этого требования вызывает необходимость переустройства существующего земляного полотна или искусственных сооружений, допускается сохранять радиусы различных значений при длине участков однообразной кривизны не менее 300 м и в исключительных случаях — не менее 200 м.
На новых магистральных скоростных линиях, особогрузонапряженных и линиях I—III категорий применять составные кривые не допускается. Составные кривые на новых линиях IV категории и подъездных путях допускается применять при соответствующем технико-экономическом обосновании.
Радиусы закрестовинных кривых должны быть не менее радиуса переводной кривой прилегающего стрелочного перевода. Размещается при этом устройство закрестовинной кривой без возвышения наружного рельса.
Радиусы кривых внутристанционных, соединительных и ходовых локомотивных путей, кривых в голове горочных сортировочных парков следует принимать не менее 200 м.