что такое процентиль в психодиагностике

Что такое процентиль?

Что такое процентиль?

Термин ″процентиль″ (percentile) часто встречается в зарубежной литературе про инвестиции и вообще в статистических исследованиях – одно из таких исследований я упоминал в этой статье. Другими вариантами русских названий являются ″персентиль″ и ″перцентиль″. Думаю, что небольшая известность термина в России не вполне заслужена, поскольку нередко именно в процентилях удобно выразить полученные результаты.

Процентиль это определенная часть выборки данных

Возьмем простой пример. Группа студентов из 200 человек пишет тест, состоящий из 100 вопросов. Проходной порог, когда тест считается сданным, составляет 2/3 правильных ответов, т.е. не менее 66. Что получается с точки зрения отдельного студента?

Допустим, Иван правильно ответил на 70 вопросов. Задачу он выполнил — тест засчитан. Результат каждого участника теста также сравнивается с числом 66: если правильных ответов больше, тест сдан. В результате формируется список сдавших и не сдавших: каждый студент проходил через это. Пока ничего нового.

Но задачу можно поставить и по-другому: нужно сравнить результаты студентов не с проходным баллом в 66 пунктов, а между собой. Зачем это нужно? В данном случае, например, для объективной оценки сложность теста, что достигается группировкой результатов.

Вернемся к Ивану, который получил 70 правильных ответов. Много это или мало по сравнению с остальными? Это и покажет процентиль.

Процентили делят всю выборку на определенные части. Например, пятый процентиль охватывает 5% объема выборки. Предположим, показатель Ивана равен пятому процентилю. Это означает, что Иван написал тест лучше, чем 5% студентов (10 человек из 200 получили от нуля до 70 баллов). Не густо, поскольку в этом случае остальные 190 человек набрали больше, чем 70. Значит, тест был очень легкий и порог в 66 баллов можно и повысить.

Но в том же самом тесте может быть и обратная ситуация: результат Ивана равен 90-ому процентилю. Это значит, что Иван написал тест лучше, чем 90% студентов. Или по другому: только 10% (20 человек) набрали более 70 правильных ответов. Следовательно, тест был весьма трудным. Преимущество метода еще и в том, что разбивкой на процентили можно сравнивать тесты с разным числом участников.

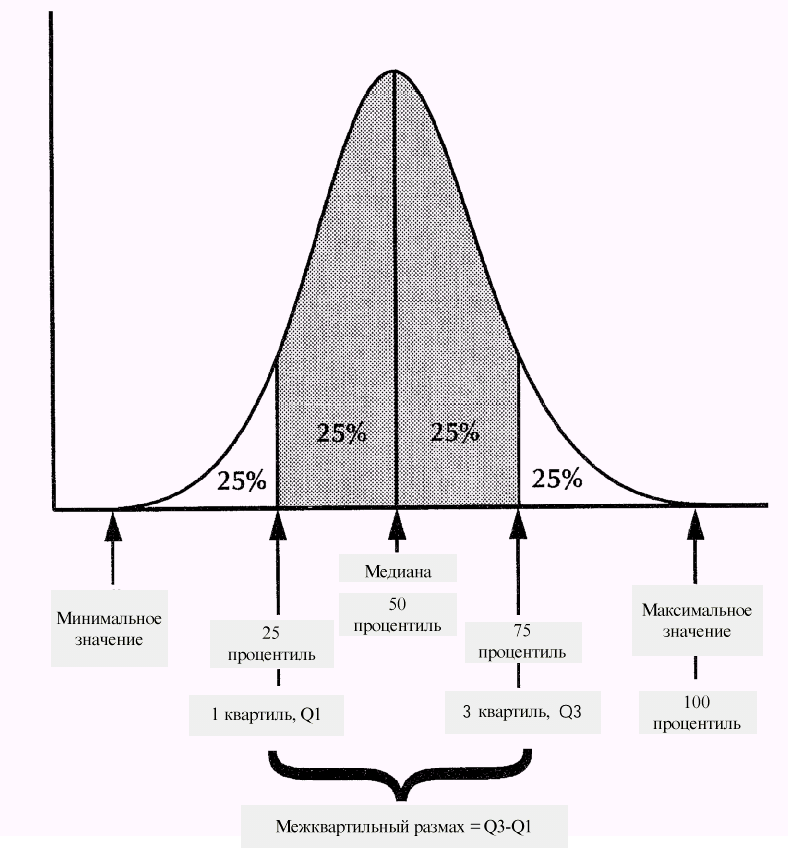
Функция Гаусса

Чем более высок процентиль, тем больше данных он включает

Расчет процентиля в Excel

Процентиль несложно вычислить по формуле:

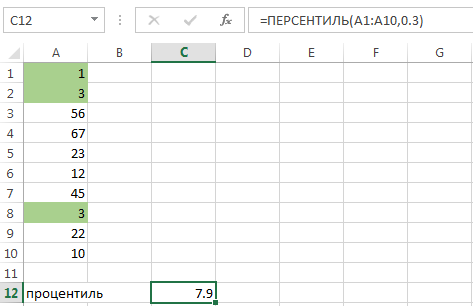
но проще обрабатывать массив данных одноименной функцией Excel. Для примера возьмем произвольную выборку полученных баллов и рассчитаем в ней процентили:

Функция PERCENTILE (ПЕРСЕНТИЛЬ) включает в себя ввод диапазона ячеек данных (А1:А10) и значения процентиля К, деленного на 100%. Т.е. в данном случае ввод 0.3 означает нахождение тридцатого процентиля. Смысл расчета: к 30-му процентилю будут относиться все результаты, меньше или равные 7.9.

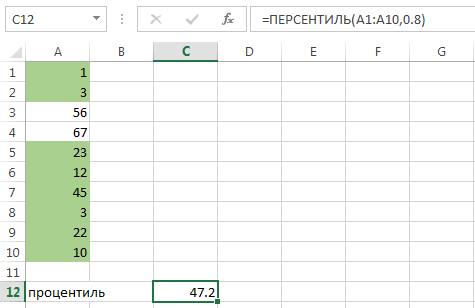
Если мы хотим узнать процентиль участника, получившего 10 баллов, то это несложно сделать, варьируя значение К до тех пор, пока значение в ячейке С12 не станет близким 10. Получится примерно 34-ый процентиль. При увеличении процентиля в выборку попадает больше табличных значений:

Итого, в 80-ый процентиль попадает уже 8 табличных значений из 10, которые меньше или равны 47.2. При этом подчеркнуть результат можно диапазоном процентилей — например, между восьмидесятым и сотым. В этом случае значения будут лежать между 47.2 и 67 (максимальным числом выборки).

Источник

ЛЕКЦИЯ № 18. Психологический диагноз

2. Шкальные оценки

Шкальные оценки — способ оценки результата теста путем установления его места на специальной шкале. Шкала содержит данные о внутригрупповых нормах выполнения данной методики в выборке стандартизации. Так, индивидуальные результаты выполнения заданий (первичные оценки испытуемых) сравниваются с данными в сопоставимой нормативной группе (например, результат, достигнутый учеником, сравнивается с показателями детей того же возраста или года обучения; результат исследования общих способностей взрослого сопоставляется со статистически обработанными показателями репрезентативной выборки лиц в заданных возрастных пределах).

Шкальные оценки в этом смысле имеют четко определенное количественное содержание и могут быть использованы при статистическом анализе. Одной из распространенных в психологической диагностике форм оценки результата теста путем соотнесения с групповыми данными является расчет процентилей.

Процентиль — процентная доля индивидов из выборки стандартизации, результат которых ниже данного первичного показателя. Шкалу процентилей можно рассматривать как совокупность ранговых градаций (см. ранговая корреляция) при числе рангов 100 и отсчете от 1-го ранга, соответствующего самому низкому результату; 50-й процентиль (PSQ) соответствует медиане (см. меры центральной тенденции) распределения результатов, Р_›50 и Р_‹50 соответственно представляют ранги результатов выше и ниже среднего уровня результата.

Процентили не следует смешивать с обычными процентными показателями. Последние представляют собой долю правильных решений из общего количества заданий теста в индивидуальном результате (см. первичные оценки). Ранги Р, и Р₁₀₀ получают соответственно самый низкий и самый высокий результаты из наблюдавшихся в выборке, однако этим рангам могут соответствовать и далеко не нулевой (ни одного правильного решения) или абсолютный (все решения правильны) показатели (например, при общем количестве 120 заданий минимальный результат, соответствующий первому рангу, может составить 6 правильных решений, в то время как максимальный результат, соответствующий рангу Р₁₀₀, будет составлять 95 правильно решенных заданий). Такая ситуация наблюдается, например, при оценке тестов скорости.

Основной недостаток процентильных шкал состоит в неравномерности единиц измерения. При нормальном распределении отдельные переменные тесно группируются в центре распределения и по мере удаления к краям рассеиваются. Поэтому равным частотам случаев вблизи центра соответствуют более короткие интервалы по оси абсцисс, расположенные по краям распределения оценок. Процентили показывают относительное положение каждого испытуемого в нормальной выборке, но не величину различий между результатами. Это создает некоторые неудобства в интерпретации индивидуальных результатов. Так, разница в первичных показателях, соответствующая интервалу Р₇₀-Р₈₀, может составить 10 баллов, а различие в количестве правильных решений в интервале рангов Р₅₀-Р₆₀ — лишь 1–3 балла.

Вместе с тем процентильные оценки обладают и рядом достоинств. Они легкодоступны пониманию пользователей психодиагностической информацией, универсальны по отношению к различным типам методик и легко рассчитываются.

Процентильные оценки не относятся к типичным шкальным показателям. Более широкое распространение в психодиагностике получили стандартные показатели, рассчитываемые на основе линейного и нелинейного преобразования первичных показателей, распределенных по нормальному или близкому к нормальному закону. При таком расчете проводится г-преобразование оценок (см. стандартизация, нормальное распределение). Чтобы определить 2-стандартный показатель, определяют разность между индивидуальным первичным результатом и средним значением для нормальной группы, а затем делят эту разность на а нормативной выборки. Полученная таким образом шкала z имеет среднюю точку М = 0, отрицательные значения обозначают результаты ниже среднего и убывают по мере удаления от нулевой точки; положительные значения обозначают, соответственно, результаты выше среднего. Единица измерения (масштаб) в шкале z равна 1а стандартного (единичного) нормального распределения.

Для преобразования полученного при стандартизации распределения первичных нормативных результатов в стандартную z-шкалу необходимо исследовать вопрос о характере эмпирического распределения и степени его согласованности с нормальным. Поскольку для большинства случаев значения показателей в распределении умещаются в пределах М ± 3σ, единицы измерения простой z-шкалы слишком велики. Для удобства оценивания применяется еще одно преобразование типа z = (x — ‹x›) / σ. Примером такой шкалы могут быть оценки тестовой батареи SAT(СЕЕВ) методики для оценки способности к обучению (см. тесты достижений). Эта r-шкала пересчитана таким образом, что средней точке соответствует значение 500, а σ = 100. Другим аналогичным примером является шкала Векслера для отдельных субтестов (см. шкала измерения интеллекта Векслера, где М = 10, σ = 3).

Наряду с определением места индивидуального результата в стандартном распределении групповых данных введение ШО направлено и на достижение другой важнейшей цели — обеспечение сопоставимости количественных результатов различных тестов, выраженных в стандартных шкалах, возможности их совместных интерпретаций, сведение оценок к единой системе.

В случае, если оба распределения оценок в сравниваемых методиках близки к нормальному, вопрос о сопоставимости оценок решается довольно просто (в любом нормальном распределении интервалам М ± nσ соответствует одинаковая частота случаев). Для обеспечения сопоставимости результатов, принадлежащих к рас-пределениям другой формы, применяются нелинейные преобразования, позволяющие придать распределению форму заданной теоретической кривой. В качестве такой кривой обычно используется нормальное распределение. Как и 160–150 в простом г-преобразовании, нормализованным стандартным показателям можно придать любую желаемую форму. К примеру, умножив такой нормализованный стандартный показатель на 10 и прибавив константу 50, получаем Т-показатель (см. стандартизация, миннесотский многоаспектный личностный опросник).

Примером нелинейно преобразованной в стандартную шкалу является и шкала станайнов (от англ. standart nine — «стандартная девятка»), где оценки принимают значения от 1 до 9, М = 5, σ=2.

Шкала станайнов получает все большее распространение, сочетая в себе достоинства стандартных шкальных показателей и простоту процентилей. Первичные показатели легко преобразуются в станайны. Для этого испытуемых ранжируют по возрастанию результатов и из них образуют группы с числом лиц, пропорциональным определенным частотам оценок в нормальном распределении тестовых результатов (табл. 14).

Источник

Ваш психолог. Работа психолога в школе.

Самое популярное

Занятие. Стандартизация результата и нормы теста
Вводные замечания
Психодиагностические методики являются измерительными инструментами. Для того чтобы измерить какой-либо мерой величину измеряемого, необходимо, чтобы были соблюдены определенные условия (К.М. Гуревич [24]).
Первое условие касается самого измерительного инструмента: он должен иметь на протяжении всего измерения одну и ту же тождественную самой себе меру. Нельзя измерять инструментом, у которого нет такой тождественной самой себе меры (например, если бы на линейке расстояния от одного деления до другого были неодинаковы на разных участках).

Второе условие – необходимо, чтобы то, что измеряется, во всех случаях оставалось одним и тем же, т.е. также было тождественно самому себе.
Как показывает далее К.М. Гуревич, соблюсти эти два условия в психодиагностических исследованиях крайне затруднительно. Вопрос стабильности измеряемых психических характеристик находится в компетенции соответствующих предметных областей психологической науки. В настоящем параграфе будут рассмотрены требования к психодиагностическим методикам, как профессиональным инструментам измерения индивидуально-психологических характеристик. К числу этих требований относятся стандартизация, надёжность и валидность.
Стандартизация – это единообразие процедуры проведения и оценки выполнения теста. Она рассматривается в двух планах: как выработка единых требований к процедуре эксперимента и как определение единого критерия оценки результатов (рис. 9.1.1).
Стандартизация процедуры проведения обследования подразумевает единообразие инструкций, бланков и других материалов обследования, способов регистрации результатов, условий проведения обследования.
Стандартизация психодиагностической методики

Рис. 9.1.1 Составляющие процесса стандартизации психодиагностической методики

При проведении психодиагностического обследования надо соблюдать следующие требования:
– инструкции следует сообщать испытуемым одинаковым образом, лучше письменно; в случае устных указаний они даются в разных группах одними и теми же словами, понятными для всех, в одинаковой манере;
– ни одному испытуемому не следует давать никаких преимуществ перед другими;
– в процессе эксперимента не следует давать отдельным испытуемым дополнительные пояснения;
– эксперимент с разными группами следует проводить по возможности в одно и то же время дня в сходных условиях;
– временные ограничения в выполнении заданий для всех испытуемых должны быть одинаковыми.
Стандартизация критериев выполнения теста осуществляется путём её проведения на большой представительной выборке испытуемых, которая ничем не отличатся от той, для которых данная методика предназначена. Такая выборка называется выборкой стандартизации. Она представляет собой меньшую по размеру точную модель генеральной совокупности. Правила формирования выборки стандартизации подробно изложены в учебном пособии «Методы психолого-педагогической оценки» [38].
Стандартизация оценки выполнения применяется в основном для тестов и опросников и включает определение нормативных данных и построение шкалы стандартных показателей.
Нормы – это статистические показатели выборки стандартизации (среднее значение и стандартное отклонение), позволяющие охарактеризовать положение обследованного индивидуума относительно выборки стандартизации. Рассчитанные на основе обследования выборки стандартизации среднее значение (обозначается латинской буквой М или греческой буквой µ – мю) и стандартное отклонение (обозначается греческой буквой σ – сигма) являются основой для разработки шкалы оценок в стандартных показателях, к которым относятся Z-показатели, Т-показатели, стены, станайны.
Z-показатели
Z-показатель – выражение шкальных показателей в единицах стандартного отклонения:

Таблица 9.1.1 Нормы теста Равена в процентилях

Источник

Лекция «Психометрические основы диагностики»

Тема «Психометричекие основы диагностики»

Стандартизация и стандартные показатели.

Диагностическая методика отличается от любой исследовательской тем, что она стандартизирована. Стандартизация — это единообразие процедуры проведения и оценки выполнения теста. Рассматривается она в двух планах:

♦ как выработка единых требований к процедуре эксперимента;

♦ как определение единого критерия оценки результатов диагностических испытаний.

Стандартизация процедуры эксперимента подразумевает унифика­цию инструкций, бланков обследования, способов регистрации резуль­татов, условий проведения обследования.

К числу требований, которые необходимо соблюдать при проведе­нии эксперимента, можно, например, отнести такие:

1) инструкции следует сообщать испытуемым одинаковым образом, как правило, письменно; в случае устных указаний они даются в разных группах одними и теми же словами, понятными для всех, в одинаковой манере;

2) ни одному испытуемому не следует давать никаких преимуществ перед другими;

3) в процессе эксперимента не следует давать отдельным испытуемым дополнительные пояснения;

4) эксперимент с разными группами следует проводить в одинако­вое, по возможности, время дня, в сходных условиях;

5) временные ограничения в выполнении заданий для всех испыту­емых должны быть одинаковыми и т. д.

Обычно авторы методики в руководстве приводят точные и подроб­ные указания по процедуре ее проведения. Формулирование таких указаний составляет основную часть стандартизации новой методи­ки, так как только строгое их соблюдение дает возможность сравнить между собой показатели, полученные разными испытуемыми.

Другим наиболее важным этапом в стандартизации методики явля­ется выбор критерия, по которому следует проводить сравнение ре­зультатов диагностических испытаний, поскольку диагностические методики не имеют заранее определенных стандартов успешности или неудачи в их выполнении.

Так, например, ребенок шести лет, выполняя тест умственного развития, получил балл, равный 117. Хорошо это или плохо? Часто ли такой показатель встречается у детей данного возраста? Количественный результат как таковой ничего не означает. Полученный дошколь­ником балл нельзя интерпретировать как показатель относительно вы­сокого, среднего или низкого развития, так как это развитие выражено в мерах, присущих данной методике, и, таким образом, абсолютного значения полученные результаты иметь не могут. Очевидно, нужно располагать точкой отсчета и какими-то дозированными мерами, что­бы с их помощью оценивать полученные при диагностировании инди­видуальные и групповые данные. Возникает вопрос, что за эту точку отсчета брать?

В традиционном тестировании такая точка добывается статистическим путем — это так называемая статистическая норма.

В общих чертах стандартизация диагностической методики, ориен­тированной на норму, осуществляется путем ее проведения на большой представительной выборке испытуемых, которая ничем не отли­чается от той, для которой данная методика предназначена. На этой группе испытуемых, называемой выборкой стандартизации, разрабатываются нормы, указывающие не только средний уровень выпол­нения, но и его относительную вариативность выше и ниже среднего уровня. В результате можно оценить разные степени успешности или неуспешности в выполнении диагностической пробы. Это позволяет определить положение конкретного испытуемого относительно выборки стандартизации.

Для вычисления статистической нормы психологи-диагносты об­ратились к приемам математической статистики.

Кроме статистической нормы, основой для сравнения, интерпретации результатов диагностических испытаний могут стать и такие показатели, как процентили.

Процентиль — это процентная доля индивидов из выборки стандар­тизации, первичный результат которых ниже данного первичного показателя.

Например, если 28 % людей правильно решат не более 15 задач в арифметическом тесте, то первичному показателю 15 соответствует 28-й про­центиль (Р₂₈). Процентили указывают на относительное положение ин­дивида в выборке стандартизации. Их также можно рассматривать, как ранговые градации, общее число которых равно 100, с той лишь разницей, что при ранжировании принято начинать отсчет сверху, т. е. с луч­шего члена группы, получающего ранг 1. В случае же процентилей от­счет ведется снизу, поэтому чем ниже процентиль, тем хуже позиция индивида.

50-й процентиль (Р₅₀) соответствует медиане — одному из показателей центральной тенденции. Процентили свыше 50 представляют показатели выше среднего, а те, которые лежат ниже 50, — сравнительно низкие показатели. 25-й и 75-й процентили известны также под названием 1-го и 3-го квартилей, поскольку они выделяют нижнюю и верхнюю четверти распределения. Как и медиана, они удобны для описания распределения показателей и сравнения с другими распреде­лениями.

Процентили не следует смешивать с обычными процентными пока­зателями. Последние являются первичными показателями и представляют собой процент правильно выполненных заданий, тогда как процентиль — это производный показатель, указывающий на долю от общего числа членов группы.

Процентильные показатели обладают рядом достоинств, в частности:

♦ их легко рассчитать и понять даже сравнительно неподготовленному человеку;

♦ их применение достаточно универсально и подходит к любому типу тестов.

Выборка стандартизации. При разработке и применении любой точки отсчета следует обращать особое внимание на выборку испыту­емых, на которой проводится стандартизация диагностической мето­дики. В математической статистике принято различать такие понятия, как генеральная совокупность (популяция) и выборка.

Всякая большая совокупность людей, которую хотели бы исследо­вать или относительно которых собираются делать выводы, называет­ся генеральной совокупностью.

Выборка — это часть или подмножество совокупности. Проводить исследование всей популяции не принято. Обычно из нее выделяют группу людей — выборку стандартизации — которая реально подверга­ется тестированию, и с ее помощью оценивается генеральная совокуп­ность. Чтобы оценки носили достоверный характер, выборка должна быть репрезентативна, представительна рассматриваемой популя­ции, т. е. ее вероятностные свойства должны совпадать или быть близ­кими к свойствам генеральной совокупности.

А. Анастази [10, т. 1] приводится пример формирования репрезентативной выборки при стандартизации шкалы Векслера. Выборка вклю­чала 1700 человек с равным количеством мужчин и женщин. Испытуе­мые в возрасте от 16 до 64 лет были распределены по семи возрастным уровням. При формировании выборки исследователи опирались на дан­ные последней переписи населения США. Учитывалось пропорциональ­ное распределение населения по географическим районам, принадлеж­ность к городскому и сельскому населению, принадлежность к белой или цветной расе, учитывались также уровень образования и профес­сия. На каждом возрастном уровне в выборку были введены один муж­чина и одна женщина, находящиеся в учреждениях для умственно от­сталых.

По мнению А. Анастази, подавляющее большинство диагностиче­ских методик стандартизовано не для столь широких популяций, как многие полагают. Трудно рассчитывать, что по какому-либо тесту имеются адекватные нормы для таких обширных популяций, как, напри­мер, «взрослые американцы-мужчины» или «американские дети 14-лет­него возраста». Выборки, ориентированные на широкие популяции, не всегда репрезентативны и чаще всего бывают смещены в тех или иных отношениях (т. е. некоторые подгруппы популяции могут быть пред­ставлены непропорционально своей численности). Так, если опре­делить популяцию как «14-летние дети», а выборку стандартиза­ции составить из 14-летних школьников, то ее нельзя рассматривать в качестве репрезентативной, поскольку не все 14-летние дети являют­ся школьниками. В этом случае лучше сузить определение популяции (т. е. определить ее как «14-летние школьники»), чем переносить нор­мы, полученные на школьниках, на популяцию 14-летних детей.

Таким образом, одним из способов обеспечения репрезентативно­сти выборки является ограничение популяции. Ограничить популяцию можно по разным признакам: по возрасту, полу, социальному проис­хождению, профессии, социально-экономическому статусу, здоровью и т. д. Такая популяция определяется как специфическая, и стандар­тизация диагностических методик осуществляется на узконаправлен­ных выборках, которые репрезентативны специфической популяции. Создатель диагностической методики должен всегда сообщать, для ка­кой специфической популяции были разработаны нормативные по­казатели.

Отбор испытуемых в выборку стандартизации осуществляется сле­дующим образом:

1) дается определение популяции с выделением в ее структуре пе­ременных, значимых и малозначимых для изучаемого психиче­ского явления (возраст, образование, профессия и т. д.);

2) популяция делится на части в соответствии со значимыми пере­менными;

3) испытуемые отбираются в случайном порядке и пропорциональ­но численности каждой значимой части совокупности. Случай­ный отбор может осуществляться по алфавиту, по таблице слу­чайных чисел или другим способом. Важно, чтобы у всех пред­ставителей популяции были равные шансы попасть в выборку стандартизации. Это условие подразумевает, что каждый выбор не зависит от остальных.

Стандартные показатели. Преимущественное использование в тестах стандартных показателей объясняется их пригодностью во многих отношениях. Такие показатели выражают отклонение индивидуального результата от средней нормы в единицах, пропорциональных стандартному отклонению распределения.

Стандартные показатели могут быть получены как линейным, так и нелинейным преобразованием первичных показателей. Если используется линейное преобразование, то при этом сохраняются соотношения между первичными показателями, поскольку они вычисляются вычитанием из каждого первичного показателя одной и той же величины с последующим делением результата на другую постоянную величину.

На рисунке –кривая нормального распределения

Z = 44+1.

Источник