что такое противоположное событие данному событию
1.2.2. Совместные и несовместные события.
Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
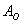
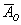
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
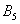
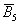
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
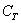
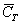
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, 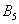
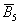
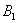
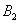
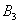
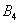
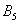
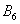
События 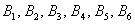
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 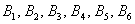
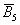
В примере с картами события 
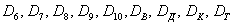
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
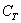
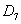
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
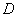
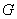
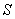
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Конспект урока по алгебре «Противоположное событие и его вероятность»(9 класс)
Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа № 38
Конспект урока по алгебре « Теория вероятностей и статистика» в 9 классе:
«Противоположное событие и его вероятность»
Учитель: Стародымова Г.Д.
Тема урока: Противоположное событие и его вероятность.
C оздание условий для овладения учащимися системой математических знаний и умений, необходимых для применения в практической деятельности, при изучении смежных дисциплин, продолжения образования .
Развивающая : способствовать формированию метапредметных умений, развивать познавательные процессы, память, воображение, наблюдательность, расширение кругозора.
Воспитательная : воспитание ответственного отношения к труду, воли и настойчивости в достижении конечных результатов, ответственного отношения к коллективной деятельности, умения оценивать свою работу и работу товарищей; воспитание культуры математической речи.
Оборудование: интерактивная доска, проектор, оценочный лист.
1.Организационный момент. Приветствие, проверка готовности учащихся к уроку.
— Здравствуйте, дети! Садитесь. Запишите в тетрадях число, классная работа.
Постановка целей и задач урока.
— Мы продолжаем изучать тему « Теория вероятностей и статистика ».
« Теория-это, когда все известно, но ничего не работает . Практика-это, когда все работает , но никто не знает почему. Мы объединяем теорию и практику: ничего не работает…и никто не знает почему!»
(Например, сколько нужно запасти порций рыбы и курицы в самолет, чтобы практически наверняка не было недовольных пассажиров?)
Я надеюсь, что вы вскоре приведете еще больше примеров задач, которые можно решить с помощью теории вероятностей.
2.Актуализация опорных знаний.
Какими можно назвать события «выигрыш» и «не выигрыш» в лотерее?
(обратными событиями, противоположными событиями ).
Приведите примеры других противоположных событий:
— студент сдаст зачет и что он его не сдаст;
— попадание и промах при выстреле;
— выпадение орла и решки при одном броске;
— отказ прибора в данном интервале времени и его исправная работа.
Решите задачу: на школьном вечере среди 100 присутствующих были распространены лотерейные билеты (каждому достался один билет), среди которых 5 выигрышных. Какова вероятность, что конкретному школьнику достался выигрышный билет? (Ответ: р=5/100=0,05) Какова вероятность, что конкретному школьнику достался невыигрышный билет? (Ответ: невыигрышных билетов 100-5=95, тогда вероятность равна 95/100=0,95)
Бросают две монеты. Чему равна вероятность появления хотя бы одного герба?
Решая эту задачу по известной схеме учащиеся приходят к выводу, что формула Р(С) = P(A) +P(B) не применима, т. к. события в этом испытании совместны. Для решения в сложившийся ситуации я рекомендую предложить учащимся избрать другой путь решения, а именно:
2) найти вероятность этого события Р(Ā) = 1/4.
-Какова же связь между вероятностями противоположных событий?
(сумма вероятности двух противоположных событий равна единице)
Сумма вероятностей противоположных событий равна 1:
Решим задачу: Вероятность того, что день будет дождливым, равна 0,7. Найдите вероятность того, что день будет ясным.
( События «день дождливый» и «день ясный» — противоположные, поэтому искомая вероятность 1 — 0,7 = 0,3)
С целью формирования нового понятия предлагаю решить задачи, для первой задачи прежде составить алгоритм решения:
Задача 1. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,05. Покупатель в магазине выбирает одну ручку. Найдите вероятность того, что эта ручка пишет хорошо.
1.Определим событие А – выбранная ручка пишет хорошо.
2.Противоположное событие 
3.Вероятность противоположного события Р( 
4. Применяя формулу вероятности противоположных событий, получаем ответ: Р(А)=1-Р( 
Задача 2. В магазине стоят два платежных автомата. Оба могут быть неисправны с вероятностью 0,0025. Найдите вероятность того, что хотя бы один автомат исправен.
Событие 

Задача 3. При изготовлении подшипников диаметром 55 мм вероятность того, что диаметр будет отличаться от заданного не более чем на 0,01 мм, равна 0,925. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 54,99, или больше, чем 55,01 мм.
Обозначим через 



Учащиеся получают 1 балл за каждую верно решенную задачу, за составленный алгоритм – 1 балл.
Физкультминутка. Проводит физорг класса.
Задача: Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.
(Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,8 2 = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128).
— Проверьте решение по образцу(слайд), исправьте допущенные ошибки, окажите взаимопомощь товарищу.
(Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,8 = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128)
Учащиеся, справившиеся с заданием, получают 2 балла.
1 . Отметь событие, являющееся противоположным событию:
Выпало одно из чисел: 1,2,3,4,5,6
Выпало одно из чисел: 1,2,3,4,6
2. Выясни, является ли следующее высказывание истинным:
(Ответ запиши в виде десятичной дроби)
4. В ящике лежат 5 белых, 10 черных и 15 красных шаров. Какова вероятность того, что наугад вынутый шар не будет белым?»
(Ответ запиши в виде десятичной дроби, дробь округлите до сотых)
3. Подведение итогов. Рефлексия.
— Какой ответ вы дадите после этого урока?
— Я надеюсь, что сегодняшний урок будет для вас еще одним аргументом в пользу изучения теории вероятностей.
— Оцените свою деятельность в оценочном листе, отметьте в листе свое настроение.
4. Домашнее задание. Инструктаж по его выполнению.
— Составьте кроссворд с математическими терминами из темы «Вероятность». На следующем занятии мы разгадаем самые интересные кроссворды.
4 и меньше баллов – подойти к учителю для консультации.
Урок по алгебре и началам математического анализа на тему: «Комбинация событий. Противоположные события»
Тема. Комбинация событий. Противоположные события
Цель урока: создание условий для овладения учащимися системой математических знаний и умений, необходимых для применения в практической деятельности, при изучении смежных дисциплин, продолжения образования.
ü Образовательная: познакомить учащихся с понятием «противоположные события», формулами зависимостей противоположных событий, совершенствовать вычислительный навык, включая округление и оценку результатов действий.
ü Развивающая: способствовать формированию метапредметных умений, развивать познавательные процессы, память, воображение, наблюдательность, расширение кругозора.
ü Воспитательная: воспитание ответственного отношения к труду, воли и настойчивости в достижении конечных результатов, ответственного отношения к коллективной деятельности, умения оценивать свою работу и работу товарищей; воспитание культуры математической речи.
II . Актуализация опорных знаний. Проверка домашнего задания.
1. Закончить предложение.
1) Событие называется случайным, если …
2) Событие называется достоверным, если …
3) Событие называется невозможным, если …
4) Приведите пример несовместных событий.
5) Приведите пример равновозможных событий.
2. Какие из следующих событий – случайные (с.), достоверные (д.), невозможные (н.):
1) черепаха научится говорить;
2) вода в чайнике, стоящем на горячей плите закипит;
3) ваш день рождения – 16 октября;
4) день рождения вашего друга – 30 февраля;
5) вы выиграете, участвуя в лотерее;
6) вы не выигрываете, участвуя в беспроигрышной лотерее;
7) вы проиграете партию в шахматы;
8) на следующей неделе испортится погода;
9) после четверга будет пятница;
10) после пятницы будет воскресенье;
11) в полночь выпадет снег, а через 24 часа будет светить солнце;
12) вас изберут руководителем фирмы.
ІІ I . Изучение нового материала.
Суммой ( объединением 
Произведением (пересечением 
Например. Пусть в опыте с бросанием игральной кости события: А – выпало число очков, кратное 2; В – выпало число очков, кратное 3. Тогда событие А + В означает, что выпало хотя бы одно из чисел 2, 3, 4, 6; событие АВ – выпало число 6.
Задача . Пусть из колоды вынимают одну карту. Рассмотрим события:
А – это король, В – это карта масти пик.
Тогда: А + В – вынут король или карта масти пик;
АВ – из колоды вынут король пик.
Для каждого события А можно рассмотреть противоположное событие Ā, которое наступит тогда и только тогда, когда событие А не наступает.
Например: А – выпадение чётного числа очков, Ā – выпадение нечетного числа очков; А – попадание в цель, Ā – промах.
№ 1118 – № 1123 (устно) стр. 341, № 1122 (7 – 10).
I V . Итог урока. Д/З. Рефлексия «Микрофон».
І V . Домашнее задание: §66, № 1119, № 1121, № 1123.
Записать по 3 примера событий: достоверных, невозможных, случайных.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Конспект урока по теории вероятности


У читель математики: Храброва Екатерина Викторовна
Предмет : теория вероятностей и статистика.
Литература : 1. Е.А. Бунимович, В.А. Булычев. Вероятность и статистика в курсе математики общеобразовательной школы: лекции 1-4,Москва Педагогический университет «Первое сентября»,2006г
2. Ю. Н. Тюрин, А. А. Макаров, И. Р. Высоцкий, И. В. Ященко Теория вероятностей и статистика, Издательство МЦНМО Москва 2011
Тема урока: « Противоположное событие и его вероятность. Диаграммы Эйлера ».
Продолжительность урока : 45 мин.
познакомить учащихся 8-го класса с понятиями противоположные события, формулами их вероятности
развивать умения решать задачи.
воспитывать аккуратность, внимательность, самостоятельность.
формировать вероятностное мышление;
способствовать запоминанию основной терминологии;
формировать умение упорядочить полученные знания для рационального применения;
способствовать развитию интереса к математике; умений применять новый материал на практике и в жизни.
Тип урока : изучение нового материала.
I . Организационный этап.
IІ. Этап подготовки учащихся к активному и сознательному усвоению нового материала:
Сообщение темы изучения нового материала.
Формулировка цели и задач изучения нового материала.
Мотивация учащихся к усвоению нового материала.
Напомним, то случайный опыт оканчивается каким-либо одним элементарным событием. Какое именно элементарное событие наступит в данном опыте – дело случая. Два разных элементарных события произойти не могут.
Можно сказать, что всякое событие А состоит из элементарных событий. Эти элементарные события называются благоприятствующими событию А.
ІІІ. Этап усвоения новых знаний:
События «выигрыш» и «не выигрыш» в лотерее являются противоположными событиями.
Определение: Событие 
Приведем несколько примеров:
1) «выигрыш» и «не выигрыш» в лотерее;
2) «появление орла» и «появление решки» в результате одного бросания;
3) «появление двух оков» и «появление не двух оков» (т.е. появление либо 1, либо 3, либо 4, либо 5, либо 6) в результате бросания игрального кубика;
4) «остановка стрелки на секторе 4» и «остановка стрелки не на секторе 4» в результате раскручивания рулетки.
Если событие В противоположно событию А, т.е В = 


Приведите примеры противоположных событий.
1) Рассмотрим следующие случайные события:
Каждое из них можно записать в виде множества благоприятных исходов:
Противоположные события будут:





Взаимно противоположные события одновременно произойти не могут, но какое-либо из них происходит обязательно. Поэтому
Р(А) + Р( 
Другими словами, сумма вероятностей взаимно противоположных событий равна единицы.
Следовательно , Р( 

Из этих формул следует, что для вычисления Р(А) достаточно знать Р( 
Какова вероятность того, что при бросании двух игральных костей на них выпадет разное (не одинаковое) число очков?
тогда 
Событию 
Вероятность каждого из этих элементарных событий, как мы знаем, равна 
Следовательно, Р( 


Тогда Р(А) = 1 – Р( 


Пусть прямоугольник изображает все элементарные события. Событие А изобразим в виде круга внутри прямоугольника. В этом случае оставшаяся часть прямоугольника изображает событие 
На рисунке с помощью диаграммы Эйлера изображены два события: событие А и противоположное событие 
Если нужно изобразить несколько событий, то рисуют несколько фигур – по одной для каждого события. При этом фигуры могут располагаться по-разному, показывая, как связаны между собой данные события.
1. В случайном эксперименте 20 элементарных событий. Событию А благоприятствуют 12 из них. Сколько элементарных событий благоприятствуют событию 
2. В некотором случайном опыте может произойти событие К. Найдите вероятность события 
а) 0,4; б) 0,85; в) 0,13; г) 
Решение: Воспользуемся формулой Р( 
а) Р( 


3. В ящике лежит 3 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не белый?
Пусть А – вынутый шар не белый.
Найдет вероятность противоположного события 
4. Монету бросают 6 раз. Событие А записано как подмножество исходов:
А = <ОРОРОР, РОРОРО>. Найдите Р ( 
5. В школьном научном обществе 10 человек: 7 мальчиков и 3 девочки. Случайным образом из членов общества выбирают двух учащихся на городскую конференцию. Какова вероятность того, что среди выбранных двух человек окажется хотя бы одна девочка?
Решение: Пусть А – среди выбранных двух человек окажется хотя бы одна девочка. Тогда событие 

N = 

число всевозможных пар, составленных их 10 школьных, равно
n = 




Итак, мы сегодня познакомились с понятием противоположные события и формулами их вероятности. Для закрепления нового понятия диктант.
Назвать событие, противоположные указанному в данном испытании.
1. При бросании игральной кости выпало четное число очков.
(«При бросании игральной кости выпало нечетное число очков» или «При бросании игральной кости не выпало четное число очков»).
2. Алеша вытащил выигрышный билет в розыгрыше лотереи.
(«Алеша вытащил билет без выигрыша» или «Алеша не вытащил выигрышный билет»)
3. После раскручивания стрелки рулетки она остановилась на секторе 2.
(«После раскручивания стрелки рулетки, она остановилась на секторе 1 или 3 или 4 » или «После раскручивания рулетки она остановилась не на секторе 2»)
4. Из ящика, в котором лежат 2 белых и 3 черных шара случайным образом вынут белый шар. («Из ящика случайным образом вынут черный шар» или «Из ящика вынут не белый шар»)
3) а) Докажите, что события А и В не могут быть противоположными, если Р(А) = 0,7, а Р(В) = 0,44. (Для того, то бы события были противоположными, сумма их вероятностей должна быть равной 1, а Р(А) + Р(В) = 0,7 + 0,44 = 1,14 не равно 1, значит события А и В не могут быть противоположными.)
б) вероятность события А равна 0,3, а вероятность события В равна 0,7. Могут ли события А и В быть противоположными. (Р(А) + Р(В) = 0,3 + 0,7 = 1, значит события А и В могут быть противоположными.
5) Бросают одну игральную кость. События А состоит в том, что:
в) выпало число очков, кратное 3.Пересислите элементарные события, благоприятствующие событию 

(А – < 3,6 >, 
7) В классе 15 мальчиков и 10 девочек. Из класса случайным образом выбирают одного ученика. Событие D – «выбрана девочка».
в) Опишите словами событие 
г) чему равна вероятность Р( 
( а) 10, б) Р( D ) = 

г) Р( 




