что такое простое число в математике 5 класс определение

Числа. Простые числа.

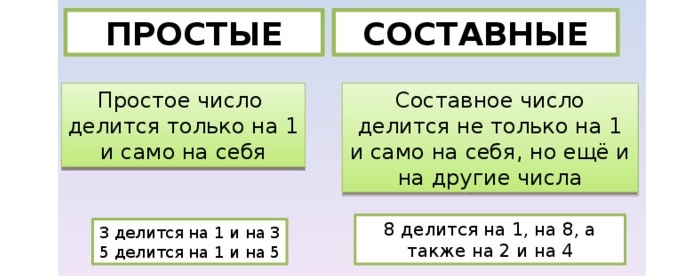
Натуральные числа, большие единицы и числа, которые не являются простыми, называют составными числами. Т.о., все натуральные числа делятся на 3 класса: единица (имеет 1 делитель), простые числа (имеют 2 делителя) и составные числа (имеют больше 2-х делителей).

Начало последовательности простых чисел выглядит так:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, …

Если представить натуральные числа как произведение простых, то это будет называться разложение на простые либо факторизация числа.

Самое большое простое число, которое известно.

Некоторые свойства простых чисел.

Допустим, p — простое, и p делит ab, тогда p делит a либо b.

Кольцо вычетов Z_n будет называться полем только в случае, если n — простое.

Характеристика всех полей — это нуль либо простое число.

Когда G — конечная группа, у которой порядок |G| делят на p, значит, у G есть элемент порядка p (теорема Коши).

Натуральное p > 1 будет простым лишь в случае, если (p-1)! + 1 можно подулить на p (теорема Вильсона).

Когда n > 1 — натуральное, значит, есть простое p: n 1 — целые взаимно простые числа, содержит нескончаемое число простых чисел (Теорема Дирихле о простых числах в арифметической прогрессии).

Любое простое число, которое большее тройки, можно представить как 6k+1 либо 6k-1, где k — натуральное число. Исходя из этого, когда разность нескольких последовательных простых чисел (при k>1) одинаковая, значит, она точно делится на шесть — к примеру: 251-257-263-269; 199-211-223; 20183-20201-20219.

Теорема Грина-Тао. Есть бесконечные арифметические прогрессии, которые состоят из простых чисел.

Ни одно простое число нельзя представить как n 2k+1 +1, где n>1, k>0. Другими словами, число, которое предшествует простому, не может быть кубом либо более высокой нечётной степенью с основанием, которое больше единицы.

Есть многочлены, у которых множество неотрицательных значений при положительных значениях переменных совпадает с множеством простых чисел. Пример:

Источник

Математика. 5 класс

Конспект урока

Простые и составные числа

Перечень рассматриваемых вопросов:

— простые и составные числа;

Простым числом называют такое натуральное число, которое больше 1 и делится только на 1 и само на себя.

Составные числа – это непростые натуральные числа больше единицы

1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС//С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 кл.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Посмотрите, на какие числа можно разделить 2 и 10.

Число 2 делится на 1 и 2.

Число 10 делится на 1, 2, 5 и 10.

По тому, на какие числа делятся натуральные числа, их можно классифицировать на простые и составные. Сегодня мы выясним, какими способами можно определить, является данное число простым или составным. Начнём с определения простых и составных чисел.

Простым числом называют такое натуральное число, которое больше 1 и делится только на 1 и само на себя.

Например, это числа 2, 3, 5 и т. д.

Составные числа – это непростые натуральные числа больше 1, Например, числа 4 и 15.

4 делится на 1, 2, 4.

15 делится на 1, 3, 5 и 15.

Важно знать, что 1 – это не простое и не составное число.

Простых и составных чисел очень много. Множество натуральных чисел состоит из простых чисел, составных чисел и единицы.

В ряду простых чисел существует самое первое число – это 2, но самого последнего нет.

Самое первое натуральное составное число – это 4, а самого последнего нет.

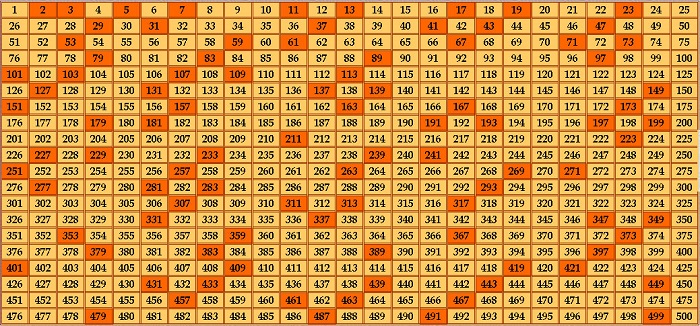
Так как простых чисел много, то для удобства составляют таблицу простых чисел. В качестве примера приведём её часть, где представлены все простые числа от 2 до 503.

Ответим с помощью неё на следующий вопрос.

Простым или составным является число 159?

Посмотрим в таблицу простых чисел, этого числа там нет, следовательно, 159 – составное число.

Выполним ещё одно задание.

Разложим составное число 234 на простые множители. Для этого воспользуемся признаками делимости на 2, 3.

39: 3 = 13 – простое число.

Следовательно, число 234 можно разложить на простые множители следующим образом:

Простые числа учёные пытались найти ещё в Древней Греции. Так, во II веке до н.э. Эратосфен составил алгоритм нахождения простых чисел до некоторого целого числа. Этот алгоритм назвали «решето Эратосфена». Суть заключается в том, что путём отсеивания составных чисел определяются простые. Опишем этот алгоритм нахождения простых чисел от 1 до 100.

Для начала запишем все числа от 1 до 100.

1 вычеркнем, т. к. это число не простое и не составное. Выделим 2 – это первое простое число – и далее вычеркнем все кратные ему числа до ста (4, 6, 8 и т. д., то есть каждое второе число). Далее отметим следующее простое число – это 3. Вычеркнем все кратные ему числа до ста (6, 9, 12 и т. д., то есть каждое третье число).

Повторяем все шаги пока возможно с остальными простыми числами. В результате получается искомая таблица простых чисел.

№ 1. Какую из цифр 2,3,1 нужно подставить в число 2_ вместо пропуска, чтобы получить простое число?

Решение. Для решения этой задачи достаточно посмотреть на таблицу простых чисел, из приведённых цифр подходит только 3, т.е. искомое простое число – 23.

№ 2. Подчеркните то число, которое делится одновременно на простые числа 5 и 7.

Варианты ответа: 35; 50; 21.

Решение. Найдём делители каждого из чисел:

К данному условию подходит только число 35, т.к. только оно имеет делитель и 5, и 7 одновременно.

Источник

Простые числа в математике

Что такое простые числа

Простые числа — натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Другими словами, число x является простым, если оно больше 1 и при этом делится без остатка только на 1 и на x.

Например, 11 — это простое число. Его можно разделить только на 1 и 11. Деление простого числа на другое приводит к тому, что остается остаток, что называют простым числом.

13 ÷ 4 = 3 (остаток 1).

Число, имеющее более двух множителей, называется составными числами. Наименьшее простое число равно 2, потому что оно делится само на себя и только на 1.

30 не является примером простого числа, потому что его можно разделить на 1,2,3,5,6,10,15,30. Таким образом, 30 является примером составного числа, поскольку оно имеет более двух факторов.

Ноль, единица и числа меньше единицы не считаются простыми числами.

Основная теорема арифметики, лемма Евклида

Основная идея теоремы арифметики — это любое целое число больше 1 либо является простым числом, либо может быть получено путем умножения простых чисел вместе.

Фундаментальная теорема арифметики (название которой указывает на ее основную важность) гласит, что любое число может быть учтено в уникальном списке простых чисел.

Простое число (2,3,5,7,11. ) против составного (4=2×2, 6=2×3, 8=2x2x2, 12=2x2x3. ).

Этот ряд примеров можно продолжить:

Таким образом, они либо простые, либо простые числа, умноженные друг на друга.

Число 42. Можем ли мы получить 42, умножив только простые числа?

Да, 2, 3 и 7 являются простыми числами, и при умножении вместе они составляют 42.

Число 7. 7 уже является простым числом

Число 22. 22 может быть получено путем умножения простых чисел 2 и 11 вместе.

Никакая другая комбинация простых чисел не будет работать.

Лемма — это, как правило, незначительное, доказанное утверждение, которое используется в качестве ступеньки к доказательству более сложной математической теории. По этой причине она также известна как «вспомогательная теорема».

В теории чисел лемма Евклида — это лемма, которая отражает фундаментальное свойство простых чисел, а именно: если простое число p делит произведение ab двух целых чисел a и b, то p должно разделить, по крайней мере, одно из этих целых чисел a и b.

Если p = 19, a = 133, b = 143, то ab = 133 × 143 = 19019, и поскольку это делится на 19, лемма подразумевает, что один или оба из 133 или 143 также должны быть. На самом деле 133 = 19 × 7.

Если предпосылка леммы не выполняется, т. е. p является составным числом, его следствие может быть либо истинным, либо ложным.

В случае p = 10, a = 4, b = 15 составное число 10 делит ab = 4 × 15 = 60, но 10 не делит ни 4, ни 15.

Это свойство является ключевым в доказательстве фундаментальной теоремы арифметики. Лемма Евклида показывает, что в целых числах неприводимые элементы также являются простыми элементами.

Таким образом, изучение чисел в основном сводится к изучению свойств простых чисел. Математики на протяжении тысячелетий довольно много выяснили о простых числах. Одно из самых известных доказательств Евклида показывает, что существует бесконечно много простых чисел.

Как определить простые числа

Сначала попробуйте разделить его на 2 и посмотреть, получится ли целое число. Если да, то оно не может быть простым числом. Если вы не получите целое число, затем попробуйте разделить его на простые числа: 3, 5, 7, 11 (9 делится на 3) и так далее, всегда делясь на простое число.

8 простых чисел до 20: 2, 3, 5, 7, 11, 13, 17 и 19.

Первые 10 простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

Таблица простых чисел до 1000:

2 — наименьшее простое число. Это также единственное четное простое число — все остальные четные числа могут быть разделены сами по себе на 1 и 2, что означает, что у них будет, по крайней мере, 3 фактора.

Один из самых известных математиков классической эпохи, Евклид, записал доказательство того, что не существует самого большого простого числа. Самое большое известное простое число (по состоянию на ноябрь 2020 года) составляет 282 589 933-1, число, которое имеет 24 862 048 цифр при записи в базе 10. До этого самым большим известным простым числом было 277 232 917-1, состоящее из 23 249 425 цифр.

За исключением 2 и 3, все остальные простые числа могут быть выражены в общей форме как 6n + 1 или 6n — 1, где n — натуральное число.

Чтобы определить, является ли число простым или составным, нужно решить пример на делимость в следующем порядке (от простого к сложному): 2, 5, 3, 11, 7, и 13. Если вы обнаружите, что число делится на одно из них, и вы знаете, что оно составное, не нужно выполнять остальные тесты.

Если число меньше 121 не делится на 2, 3, 5 или 7, оно простое; в противном случае оно составное.

Если число меньше 289 не делится на 2, 3, 5, 7, 11, или 13, это простое число; в противном случае оно составное.

Примеры решения задач

Является ли 19 простым числом или нет?

Как понять, что число простое можно двумя способами.

Формула для простого числа равна 6n + 1

Запишем данное число в виде 6n + 1.

Проверьте на наличие факторов 19

Следовательно, с помощью обоих методов докажем, что 19 имеет только два фактора 1 и 19, что означает простое число.

53 — это простое число или нет?

Как доказать, что число простое, используя приведенную ниже формулу. Чтобы узнать простые числа, превышающие 40, можно:

32 + 3 + 41 = 9 + 3 + 41 = 53

53 имеет только факторы 1 и 53.

Итак, 53 является простым числом по обоим методам.

Является ли число простым или составным?

Число 185 заканчивается на 5, поэтому оно делится на 5. Оно составное.

Как проверить простое ли число 243?

Число 243 заканчивается нечетным числом, поэтому оно не делится на 2. Он не заканчивается на 5 или 0, поэтому он не делится на 5. Его цифровой корень равен 9 (потому что 2 + 4 + 3 = 9), так что оно делится на 3.

Источник

Простые числа – это натуральные числа, их можно разделить только на два значения: единицу и себя. К натуральным относят те, которые используются во время счета, поэтому должно выполняться требование, чтобы они были положительными и целыми. Делители также не должны быть отрицательными и дробными.

Они широко применяются в криптографии, когда необходимо закодировать важную информацию от посторонних глаз. Шифрование касается каждого человека, так как используется в создании электронной почты, банковских карт. Даже мобильная связь защищается кодами.

Кроме того, используются на системах, защищающих транспортные средства от угонщиков, создают преграду для атак вирусов и взломов компьютерных сайтов. При попытке продолжить разложение простых чисел или определить закономерность появления, возникают новые способы математических расчетов.

Математика предлагает начинать знакомиться с данными понятиями в средней школе, в 5 или в 6 классе.

Проверка на принадлежность к определенному множеству достаточно простая:

Простые числа можно делить только на 1 и на такое же число. Например 3 и 7 — простые числа, 3 делится на 1 и на 3, 7 делится на 1 и на 7.

Составные числа можно делить не только на себя и единицу. При этом не должно получаться остатка. Они делятся на одно или несколько значений. Например, 8 и 6 относят к составным. Восьмерка делится на 1, 2, 4, 8; шестерка – на 1, 2, 3 и 6.

Определение простых чисел позволяет исключить из их ряда единицу. Она характеризуется наличием только одного делителя, не являющегося отрицательным значением. Получить ее можно, используя только один способ, умножив саму на себя.

Простые двузначные числа определяются по внешнему виду:

Если оканчиваются четной цифрой, то точно являются составными. То же касается и значений, имеющих больше двух знаков.

Если на конце находится цифра 5, то она входит в число делителей.

Такие простые способы помогают легко классифицировать многозначные показатели.

Некоторые двузначные вводят в заблуждение с первого взгляда, если оканчиваются на единицу. Кажется, что разложить на множители их невозможно. Но есть исключения, например: 21, 81. Чем дальше, тем больше отклонений от этой закономерности.

Последовательность простых чисел

Есть целые алгоритмы, помогающие получать новое, ранее неизвестное значение.

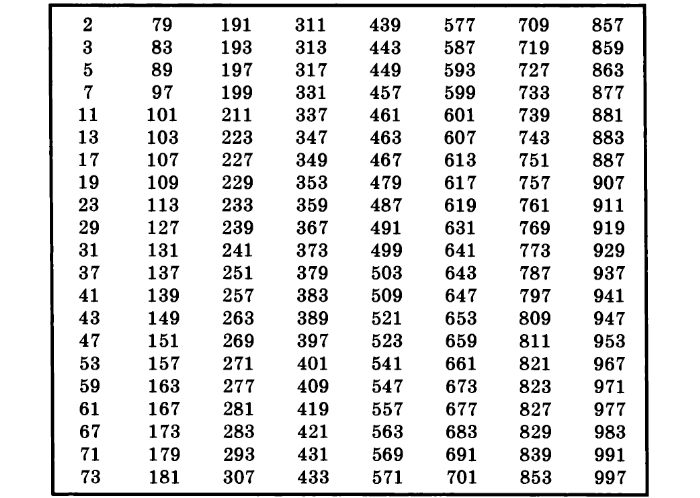
Существуют таблицы, в которых собраны найденные числа, имеющие не больше двух делителей, например, до 200, 1000 или больше.

Последовательность можно продолжать бесконечно, начинается она так: 2, 3, 5, 7, 11, 13, 17, 19 и т. д.

Наименьшее и наибольшее простое число

Самым меньшим значением, делящимся на себя и 1, является 2. Это единственное простое значение, являющееся четным. Остальные всегда делятся на два, то есть получают третий делитель.

Простых чисел много и их количество стремится к бесконечности, потому узнать самое большое невозможно.

Нескончаемость ряда была доказана еще до нашей эры Евклидом. Он предложил перемножить все известные исследуемые значения и прибавить к ним единицу.

При его делении в любом случае будет оставаться остаток, то есть отнести к составным невозможно. Что противоречит тому факту, что были использованы все известные простые числа, в том числе и самое большое. Значит, предположение о конечности ряда является неверным.

В настоящее время известно значение, имеющее около 25 миллионов знаков. Оно относится к наибольшему из открытых наукой, это 2 82 589 933

Множество простых чисел

Множествами называются совокупности элементов, объединенных в одно целое общими свойствами.

Для изучаемых объектов к ним относятся:

принадлежность к натуральным;

наличие максимум двух делителей.

Простые числа можно определить, используя решето Эратосфена. Нужно выписать в ряд все значения, с которыми предстоит работать. Выбрать самое маленькое и вычеркнуть его, затем продолжать действие, убирая кратные ему.

Например, в ряду от 1 до 100 первым таким объектом будет 2. Поэтому и вычеркивать нужно значения, кратные двойке, то есть те, которые делятся на нее.

По окончании из оставшихся выбрать новое простое, искать кратные ему и также убирать. Повторять, пока это представляется возможным.

В итоге, все составные окажутся зачеркнутыми.

Эратосфен использовал свое открытие следующим образом. Он брал папирус, записывал на нем необходимые значения, при отборе прокалывал неподходящие острым предметом (отсюда название «решето Эратосфена»). Поэтому они как будто просеивались через сито, и в списке оставались видимыми только необходимые.

Некоторые свойства простых чисел

Выделяют свойства, объединенные в теоремы, постулаты. Многие являются основой математических правил, используемых в настоящее время.

Изучением занимается теория чисел, при использовании формул простые числа обозначаются буквой n.

Известны следующие правила:

Если рассматривать два простых числа (n), одно из которых делится на другое, то можно утверждать, что они равны.

Все являются нечетными, за исключением двойки.

Можно выделить пары, разница между которым равна 2. При их сложении получается значение, кратное трем. Их так и называют парными или близнецами. Исключение составляют две первые цифры в ряду, 3 и 5, так как сумму, полученную при их сложении, нельзя разделить на 3.

Для каждого натурального значения (N), большего единицы, существует n, превышающее его. При этом удвоенное натуральное будет больше n.

Если одно из двух N делится на n, то их произведение также будет делиться на него.

Любое N, за исключением единицы, можно отнести к n или представить в виде их произведения.

Если взять составное число и разложить его на множители n, то среди них окажется один, квадрат которого будет меньше первоначального составного.

Некоторые n имеют пары, которые можно найти, перевернув n наоборот. Например, 13 и 31, 37 и 73. То же самое касается трехзначных n: 107 и 701, 709 и 907.

Если N возвести в степень, представленную n, а затем вычесть N, то полученное значение будет делиться на используемое n. Это правило представляет собой малую теорему Ферма.

Действия с простыми числами

Можно использовать разные арифметические действия, складывать, умножать, вычитать, делить. Простые числа могут являться основанием и показателем степени.

Извлечь корень из них невозможно.

Таблица простых чисел до 1000

Таблица простых числе до 10000

Источник

Что такое Простые числа

Простые числа — это натуральные числа, больше единицы, которые делятся без остатка только на 1 и на само себя. Например: 2, 3, 5, 7, 11, 13, 17, 19, 23. Единица не является ни простым числом, ни составным.

Последовательность простых чисел начинается с 2 и является бесконечной; наименьшее простое число — это 2 (делится на 1 и на самого себя).

Составные числа — это натуральные числа, у которых есть больше двух делителей (1, оно само и например, 2 и/или 3); это противоположность простым числам. Например: 4, 6, 9, 12 (все делятся на 2, на 3, на 1 и на само себя).

Все натуральные числа считаются либо простыми, либо составными (кроме 1).

Натуральные числа — это те числа, которые возникли натуральным образом при счёте предметов; например: 1, 2, 3, 4. (нет ни дробей, ни 0, ни чисел ниже 0).

Зачастую множество простых чисел в математике обозначается буквой P.

Простые числа до 1000

Как определить, является ли число простым?

Очень простой способ понять, является ли число простым — нужно его разделить на простые числа и посмотреть, получится ли целое число. Сначала нужно попробовать его разделить на 2 и/или на 3. Если получилось целое число, то оно не является простым.

Если после первого деления не получилось целого числа, значит нужно попробовать разделить его на другие простые числа: 5, 7, 11 и т. д. (на 9 делить не нужно, т. к. это не простое число и оно делится на 3, а на него вы уже делили).

Более структурированный метод — это решето Эратосфена.

Решето Эратосфена

Это алгоритм поиска простых чисел. Для этого нужно:

Те числа, которые не будут вычеркнуты в конце этого процесса, являются простыми.

Взаимно простые числа

Это натуральные числа, у которых 1 — это единственный общий делитель. Например:

Число Мерсенна

Простое число Мерсенна — это простое число вида:

До 1536 г. многие считали, что числа такого вида были все простыми, пока математик Ульрих Ригер не доказал, что 2 (^11) – 1 = 2047 было составным (23 x 89). Затем появились и другие составные числа (p = 23, 29, 31, 37 и др.).

Например, для p = 23 это 2 (^23) – 1 = 8 388 607; И 47 x 178481 = 8 388 607, значит оно составное.

Почему 1 не является простым числом?

Российские математики Боревич и Шафаревич в своей знаменитой работе «Теория чисел» (1964 г.) определяют простое число как p (элемент кольца D), не равен ни 0, ни 1. И p можно называть простым числом, если его невозможно разложить на множители ab (т.е. p = ab), притом ни один из них не является единицей в D. Так как 1 невозможно представить ни в одном, ни в другом виде, 1 не считается ни простым числом, ни составным.

Почему 4 не является простым числом?

Простое число — это натуральное число, больше единицы, которое делится без остатка на 1 и на само себя. Т. к. 4 можно разделить на 1, на 2 и на 4, из-за деления на 2 оно не является простым.

Самое большое простое число

21 декабря 2018 года Great Internet Mersenne Prime Search (проект, целью которого является открытие новых простых чисел Мерсенна) обнаружил новое самое большое известное простое число:

Новое простое число также именуется M82589933 и в нём более чем на полтора миллиона цифр больше, чем в предыдущем (найденном годом ранее).

Источник

• ← что такое бронепленка для смартфона
• что такое виндовс бут менеджер в биосе →