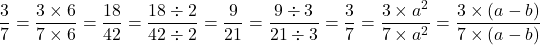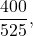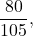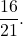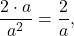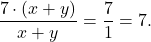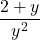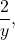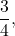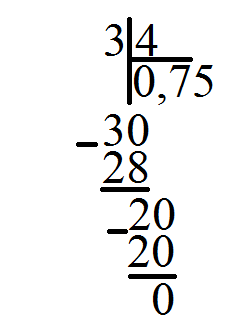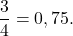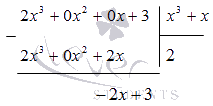что такое простейший вид дроби

Виды дробей

В математике дробь вводиться для отображения части целого числа. Например, одна вторая или половина, одна четвертая или четверть, две пятых и т.д. Все дроби можно разделить на три вида:

1. Количество частиц, на которые делится пицца 8.

2. Количество кусков, которые мы берем 5.

Основное свойство простой дроби.

Если числитель и знаменатель какой — либо дроби умножить или разделить на одно и тоже число, то значение дроби не изменится:

То есть, таким образом можно получить бесконечное количество записей одного и того же дроби.

Вопрос в том, как это свойство дроби используется на практике. Например, мы имеем дробь

разделим числитель и знаменатель этой дроби на пять и получим дробь

а если знаменатель и числитель снова разделить на 5, то вообще получим дробь:

Понятно, что работать с последней дробью гораздо удобнее и легче, чем с начальной, хотя величины обеих дробей одинаковы. Процедура деления числителя и знаменателя на одно и тоже число, описанная в примере выше, называется сокращением дроби и для простоты вычислений ее, по возможности, нужно проводить всегда.
Так же можно сокращать дробь на выражения:

И в старших классах, кроме двух чисел, нужно уметь сокращать именно выражения. Однако многие старшеклассники, взяв на вооружение процедуру сокращения, начинают применять ее там, где это недопустимо. Например, дробь вида

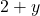
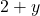
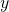
нельзя сократить, поскольку не делится ни на одно число, кроме всего выражения в целом на себя . Но старшеклассника это может не остановить, и в знаменателе и числителе будет сокращен, таким образом дробь превратится в

что для учителя будет равноценно неумению работать с дробями вообще.

Правильная и неправильная простые дроби.

3.Дробь .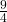

Преобразование десятичной дроби в простую и наоборот.

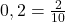
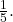
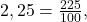
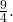
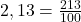
Для того, чтобы перейти от десятичной к простой дроби нужно записать десятичную дробь так как она читается, но з помощью числителя и знаменателя, а затем, по возможности, провести процедуру сокращения. Например, и после сокращения на 2 получим
и после сокращения на 25 получим Число после перевода в простую дробь сократить нельзя, так что это окончательная форма записи.

Часто приходится переводить простую дробь в десятичную, в частности для записи ответов в тестах. Что делать, если, решив задачу, получили результат в виде простой дроби

нужно, как учили в начальной школе, разделить в столбик одно число на другое.

Как видно из результатов деления, получим

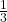
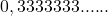
Если попытаться, например, дробь перевести в десятичную, то есть выполнить процедуру деления в столбик, то получим число и так тройки до бесконечности. Поэтому можно сделать вывод, что любая десятичная дробь переводится в обычную (простую) дробь.

Какой же формой записи дроби пользоваться лучше? Конечно же, это зависит от ситуации. Например, если у вас есть задача, где дроби находятся во всех трех видах, в таком случае надежнее перевести все эти дроби в обычные и затем проводить вычисления. Если же в задании предлагается посчитать десятичные 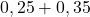дроби, то конечно же переходить к простым дробям не требуется. То есть мы выбираем тот способ решения, что является наиболее удобным.

Источник

Разложение дроби на простейшие

Для закрепления материала будут рассмотрены несколько примеров и рассмотрена теория по разложению дробей на простейшие. Подробно рассмотрим метод неопределенных коэффициентов и метод частных значений, изучим всевозможные комбинации.

Простые дроби имеют название элементарных дробей.

Типы дробей

При упрощении выражения быстрее выполняются вычислительные функции. Представление дробно-рациональной дроби как суммы простейших дробей аналогично. Для этого применяют ряды Лорана для того, чтобы разложить в степенные ряды или для поиска интегралов.

Когда степень числителя многочлена меньше степени многочлена в знаменателе, имеет место разложение на простейшие дроби. Иначе применяется деление для выделения целой части, после чего производят разложение дробно-рациональной функции.

Применим деление углом. Получаем, что

Отсюда следует, что дробь примет вид

Алгоритм метода неопределенных коэффициентов

Для того, чтобы правильно произвести разложение, необходимо придерживаться нескольких пунктов:

Рассмотрим на нескольких примерах:

P 4 x + Q 4 ( x 2 + p x + q ) 4 + P 3 x + Q 3 ( x 2 + p x + q ) 3 + P 2 x + Q 2 ( x 2 + p x + q ) 2 + P 1 x + Q 1 x 2 + p x + q + + R 2 x + S 2 ( x 2 + r x + s ) 2 + R 1 x + S 1 x 2 + r x + s

Приведение полученной суммы простейших дробей при наличии неопределенного коэффициента к общему знаменателю, применяем метода группировки при одинаковых степенях х и получаем, что

Необходимо постоянно выполнять проверки. Это способствует тому, что приведение к общему знаменателю получит вид

Методом неопределенных коэффициентов считают метод разложения дроби на другие простейшие.

Использование метода частных значений способствует представлению линейных множителей таким образом:

По условию имеем, что степень многочлена числителя меньше степени многочлена знаменателя, тогда деление выполнять не нужно. Необходимо перейти к разложению на множители. для начала необходимо выполнить вынесение х за скобки. Получим, что

x 1 + x 2 = 5 x 1 · x 2 = 6 ⇔ x 1 = 3 x 2 = 2

Имея такой знаменатель, дробь раскладываем на простейшие дроби с неопределенными коэффициентами. Выражение примет вид:

Полученный результат необходимо приводить к общему знаменателю. Тогда получаем:

После упрощения придем к неравенству вида

Метод коэффициентов и метод частных значений отличаются только способом нахождения неизвестных. Данные методы могут быть совмещены для быстрого упрощения выражения.

По условию имеем, что степень числителя многочлена меньше знаменателя, значит зазложение примет вид

Производим приведение к общему знаменателю. Имеем, что

Приравняем числители и получим, что

157 = 8 C 3 ⇒ C 3 = 157 8

Поэтому подставим полученный значения в числитель, тогда

Раскроем скобки для того, чтобы привести подобные слагаемые с одинаковыми степенями. Придем к выражению вида

Итог решения – это искомое разложение дроби на простейшие вида:

При непосредственном применении метода неопределенных коэффициентов необходимо было бы решать все пять линейных уравнений, объединенных в систему. Такой метод упрощает поиск значения переменных и дальнейшее решение в совокупности. Иногда применяется несколько методов. Это необходимо для быстрого упрощения всего выражения и поиска результата.

Источник