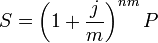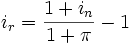что такое простая процентная ставка

Простая процентная ставка

Процентная ставка (англ. interest rate ) — это сумма, указанная в процентном выражении к сумме кредита, которую платит получатель кредита за пользование им в расчете на определенный период (месяц, квартал, год).

С позиции теории денег, процентная ставка — это цена денег как средства сбережения.

Содержание

Простые, сложные и непрерывно начисляемые проценты

При многократном начислении простых процентов начисление делается по отношению к исходной сумме и представляет собой каждый раз одну и ту же величину. Иначе говоря,

,

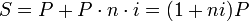
В этом случае говорят о простой процентной ставке.

При многократном начислении сложных процентов начисление каждый раз делается по отношению к сумме с уже начисленными ранее процентами. Иначе говоря,

(при тех же обозначениях).

В этом случае говорят о сложной процентной ставке.

В этом случае говорят о номинальной процентной ставке. Сравнение сложных процентных ставок с разными интервалами начисления производят при помощи показателя годовая процентная доходность(APY).

В этом случае номинальную процентную ставку δ называют сила роста.

Реальная и номинальная ставка

Различают номинальную и реальную процентную ставку.

Реальная процентная ставка — это процентная ставка, очищенная от инфляции.

Взаимосвязь реальной, номинальной ставки и инфляции в общем случае описывается следующей (приближённой) формулой:

Ирвинг Фишер предложил более точную модель взаимосвязи реальной, номинальной ставок и инфляции, выражаемую названной в его честь формулой Фишера:

Легко видеть, что при небольших значениях уровня инфляции π результаты мало отличаются, но если инфляция велика, то следует применять формулу Фишера.

Согласно Фишеру, реальная процентная ставка численно должна быть равна предельной производительности капитала.

Ссылки

См. также

Литература

Полезное

Смотреть что такое «Простая процентная ставка» в других словарях:

Простая процентная ставка — процентная ставка, которая применяется к одной и той же, начальной сумме на протяжении всего срока ссуды. Обычно простая процентная ставка используется для начисления выплат и процентов по краткосрочным ссудам со сроком до одного года. См. также … Финансовый словарь

Переменная простая процентная ставка — процентная ставка, которая применяется к одной и той же, начальной сумме на протяжении всего срока кредита; но которая может изменяться в определенные моменты времени в течение срока ссуды. См. также: Плавающие процентные ставки Финансовый… … Финансовый словарь

Учётная ставка — финансовый термин, финансовая категория, употребляемая для характеристики следующих процессов, связанных с кредитованием[1]: Под учётной ставкой понимается процентная ставка, по которой Центральный банк страны предоставляет кредиты коммерческим… … Википедия

Учетная ставка — Учётная ставка (англ. Discount rate) это сумма, указанная в процентном выражении к величине денежного обязательства (векселя), которую взимает приобретатель обязательства. Фактически, учётная ставка это цена, взимаемая за приобретение… … Википедия

ПРОЦЕНТ — INTERESTЦена (ссуды) денег; плата за заимствование денег; сумма, уплачиваемая должником кредитору за пользование деньгами последнего. П. выражается в виде годовой процентной ставки от общей суммы кредита. Так, процентная ставка 6% означает, что… … Энциклопедия банковского дела и финансов

Nonfarm Payrolls — (Количество новых рабочих мест вне сельского хозяйства) Nonfarm Payrolls это макроэкономический показатель занятости населения США вне сферы сельского хозяйства Макроэкономический показатель занятости Nonfarm Payrolls, количество рабочих мест вне … Энциклопедия инвестора

Макроэкономическая статистика — (Macroeconomic statistics) Понятие макроэкономической статистики, виды статистических показателей Информация о понятии макроэкономической статистики, виды статистических показателей Содержание >>>>>>>>>>>> … Энциклопедия инвестора

Недвижимость — (Real estate) Определение недвижимости, виды недвижимости, аренда и продажа недвижимости Информация о понятии недвижимость, виды недвижимости, аренда и продажа недвижимости, налогообложение и страхование Содержание – это вид имущества,… … Энциклопедия инвестора

Капитал — (Capital) Капитал это совокупность материальных, интеллектуальных и финансовых средств, используемых для получения дополнительных благ Определение понятия капитала, виды капитала, рынок капитала, кругооборот капитала, проблема оттока… … Энциклопедия инвестора

Кэрри-трейд — (Carry trade) Кэрри трейд это стратегия на рынке Forex, основанная на покупке/продаже национальных валют Кэрри трейд: определение и понятие, валютные пары, стратегии, основы, выгоды и риски, правила торговли, критерии и механика доходных… … Энциклопедия инвестора

Источник

Банковский процент

Банковский процент представляет собой не что иное, как плату за пользование заемными денежными средствами. В гражданском обороте самые известные случаи применения процента – это плата за кредит и плата за депозит. В обоих случаях в отношениях присутствуют два субъекта, один из которых – всегда банковское учреждение, которое на основании определенных методик экономических расчетов определяет размер банковского процента по конкретному виду операций.

Виды банковского процента

В практике осуществления банковской деятельности проценты различают несколько видов:

Ссудный процент – эта та сумма, которая начисляется заемщику за пользование кредитными средствами. Депозитный процент по сути то же самое, что и ссудный, но заемщиком в данном случае выступает банковское учреждение, которое за пользование вашими деньгами оплачивает вам вознаграждение в виде этого самого депозитного процента.

Дисконтный процент предполагает размер скидки от какой либо суммы в денежной операции. Учетный представляет собой определяемую Центробанком ставку, по которой это учреждение выдает другим банкам заемные средства.

Расчет банковских процентов

В финансовой практике принято выполнять расчет банковских процентов в годовом выражении. Это означает, что если банк указывает, что ставка принимаемых на депозит средств составляет, например, 10% годовых, вы получаете сумму, большую на эти 10%, начисленную в течении года. Если вам необходимо просчитать, сколько это будет получаться в месяц или в день – просто разделите процентную ставку на нужный вам период времени. Чтобы узнать, сколько вы получите за месяц, нужно 10% разделить на 12 (число месяцев в году). А для расчета процента в сутки необходимо будет процентную ставку разделить уже на 365 (количество дней в году).

Простой и сложный банковские проценты

Начисление банковских процентов может выполняться двумя способами, получившими название простой и сложный процент. В первом случае понимается, что за основу расчетов всегда в течении срока договора принимается сумма кредита (депозита). Сложный процент учитывает, ч то в каждом последующем периоде сумма, на которую насчитывается процент, увеличивается на размер процентов, полученных в предыдущем период.

Традиционно более выгодными принято считать депозиты по которым банк начисляет сложные проценты. По кредитам ситуация обратная. Выгодным считается процент, рассчитываемый не на всю сумму кредита, а на остаток невозвращенных банку денежных средств.

Расчет банковской процентной ставки

Перед подписанием кредитного договора желательно понимать, какие суммы придется выплачивать, поэтому важен правильный расчет банковской процентной ставки. Многие онлайн-банки предлагают на своих сайтах заемщику калькулятор для этих расчетов, но на самом деле применить его не так и просто, но возможно сделать приблизительный расчет.

Многие методы расчета банковской процентной ставки сложны и требуют математических знаний. Поэтому остановимся на более простых способах. Если сложить все предложенные в списке платежи, то можно посчитать приблизительный процент, который придется выплатить за заемные средства:

Для правильного расчета следует учитывать разные обстоятельства, которые могут возникнуть в момент пользования заемными деньгами, например, досрочное погашение, пени, штрафы и многое другое.

Некоторые клиенты банка, наоборот, доверяют кредитной организации на хранение свои финансы. Банк за это выплачивает процент, зависит его размер от многих факторов.

Процентная ставка в брокерских компаниях

Брокерская компания является посредником между продавцом и покупателем. Если раньше сберегательными операциями занимались только банки, то теперь все популярнее становятся подобные услуги в других учреждениях. Активы клиента в брокерской конторе тоже могут иметь сберегательный характер. Свободные денежные средства на депозите клиента брокер может использовать в своих целях и за это заплатить клиенту.

При кредитовании выделяют несколько особенностей банковского процента

Заемщиком выплачивается в кредитное учреждение процентная ставка, на сегодняшний день при кредитовании выделяют несколько особенностей банковского процента:

Каждый из них предназначен для определенных функций: сберегательной, регуляторной и перераспредели тельной. На расчет процентной ставки банка влияет множеств различных факторов.

От чего зависит размер банковского процента

В настоящий момент существует единая формула расчета процентной ставки по депозитному счету. Необходимо понимать, от чего зависит размер банковского процента и учитывать, что различные факторы могут его скорректировать:

М = D * (1 + r/100* t/360).

М – сумма полученная клиентом в конце срока вложения денежных средств;

r – процентная ставка банка;

t – количество дней, на которое клиент доверяет свои финансы банку.

В финансовом мире считается, что в каждом месяце 30 дней.

Пример: положить в банк 100000 рублей под 3% годовых сроком на 6 месяцев.

100000 * (1 + 3%/100 * 180/360) = 100000 * (1+ 0,03 * 0,5) = 100000 * 1,015= 101500

Предложенная формула подходит только для вкладов, процент на которые начисляется один раз в год. Если проценты на вклад зачисляются несколько раз в год, например, каждый месяц, то придется рассчитывать проценты по сложной банковской формуле:

M = D * (1 + r/100*30/360)^(360/30).

Виды банковских рисков

Виды рисков финансовых учреждений разделяются на общие и банковские, достаточно сложно разграничить их между собой. В процессе функционирования предприятие сталкивается с разными проблемами. В специализированной литературе виды банковских рисков группируются по финансовым операциям:

Риски бывают в любом предприятии, поэтому для банка важно не избежать их, а предвидеть и, как следствие, снизить угрозу до минимума.

Источник

Процентная ставка

Проценты — основные понятия

Процент — одна сотая от заранее оговоренной базы (то есть база соответствует 100%).

первоначальная сумма долга
(дни)	фиксированный промежуток времени, к которому приурочена процентная (учетная) ставка (как правило, один год — 365, иногда 360 дней)
процентная (учетная) ставка за период
срок долга в днях
срок долга в долях от периода
сумма долга в конце срока

Процентная ставка

Процентная ставка — относительная величина дохода за фиксированный отрезок времени. Отношение дохода (процентных денег — абсолютная величина дохода от представления денег в долг) к сумме долга.

Период начисления — это временной интервал, к которому приурочена процентная ставка, его не следует путать со сроком начиления. Обычно в качестве такого периода принимаю год, полугодие, квартал, месяц, но чаще всего дело имеют с годовыми ставками.

Капитализация процентов — присоединение процентов к основной сумме долга.

Наращение — процесс увеличения суммы денег во времени в связи с присоединением процентов.

Дисконтирование — обратно наращению, при котором сумма денег, относящаяся к будущему уменьшается на величину соответствующую дисконту (скидке).

Величина называется множителем наращения, а величина — множителем дисконтирования при соответствующих схемах.

Интерпретация процентной ставки

При схеме «сложных процентов» (для целых ) исходной базой для начисления процентов в течение всего срока на каждом периоде применения процентной ставки является наращенная за предыдущий период сумма долга.

Интерпретация учетной ставки

При схеме «сложных процентов» (для целых ) (сложный дисконт) — исходной базой для начисления процентов в течение всего срока на каждом периоде применения учетной ставки является сумма долга в конце каждого периода.

Простая и сложная процентные ставки

Известны две основные схемы начисления процентов в финансовых операциях.

В первой схеме применяются так называемые простые процентные ставки.

Простыми называются такие процентные ставки, которые применяются к одной и той же первоначальной сумме па протяжении всей финансовой операции.

Во второй схеме используются сложные процентные ставки.

Сложными называются ставки, применяемые после каждого интервала начисления к сумме первоначального долга и начисленных за предыдущие интервалы процентов.

«Прямые» формулы

Простые проценты	Сложные проценты
— процентная ставка			наращение
— процентная ставка			дисконтирование (банковский учет)

«Обратные» формулы

Простые проценты	Сложные проценты
— процентная ставка			дисконтирование (математический учет)
— процентная ставка			наращение

Переменная процентная ставка и реинвестирование вкладов

— при схеме простых процентов

— при схеме простых процентов

Рыночная процентная ставка как важнейший макроэкономический показатель

Важным макроэкономическим показателем выступает процентная ставка. Процентная ставка — это плата за деньги, предоставляемые в кредит. Были времена, когда законом не допускалось вознаграждение за то, что неизрасходованные, заемные деньги давали в заем. В современном мире широко пользуются кредитами, за пользование которыми устанавливается процент. Поскольку процентные ставки измеряют издержки использования денежных средств предпринимателями и вознаграждение за неиспользование денег потребительским сектором, то уровень процентных ставок играет значительную роль в экономике страны в целом.

Очень часто в экономической литературе пользуются термином «процентная ставка», хотя существует множество процентных ставок. Дифференциация процентных ставок связана с риском, на который идет заимодатель. Риск возрастает с увеличением срока кредита, так как становится выше вероятность того, что деньги могут потребоваться кредитору раньше установленной даты возврата ссуды, соответственно повышается процентная ставка. Она увеличивается, когда за кредитом обращается малоизвестный предприниматель. Мелкая фирма уплачивает более высокую процентную ставку, чем крупная. Для потребителей процентные ставки также варьируются.

Однако как бы ни отличались ставки процента, все они находятся под воздействием рыночного механизма: если предложение денег уменьшается, то процентные ставки увеличиваются, и наоборот. Именно поэтому рассмотрение всех процентных ставок можно свести к изучению закономерностей одной процентной ставки и в дальнейшем оперировать термином «процентная ставка»

Различают номинальные и реальные процентные ставки

Реальная процентная ставка определяется с учетом уровня инфляции. Она равна номинальной процентной ставке, которая устанавливается под воздействием спроса и предложения, за вычетом уровня инфляции:

Если, например, банк предоставляет кредит и взимает при этом 15%, а уровень инфляции составляет 10%, то реальная процентная ставка равна 5% (15% — 10%).

Способы начисления процентов:

проценты начисляются в конце каждого интервала начисленияссудный процент

Простая процентная ставка

Сложная процетная ставка

Начисленные за весь срок проценты:Наращенная сумма

Простая процентная ставка

График роста по простым процентам

Ситуация, когда срок ссуды меньше периода начисления

Пример. Ссуда в размере 1 млн.рублей выдана 20 января до 5 октября включительно под 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? Рассчитать в трех вариантах подсчета простых процентов.

Для начала определим число дней ссуды: 20 января это 20 день в году, 5 октября — 278 день в году. 278 — 20 = 258. При приближенном подсчете — 255. 30 января — 20 января = 10. 8 месяц умножить на 30 дней = 240. итого: 240 + 10 + 5 = 255.

Точные проценты с точным числом дней ссуды (365/365)

Обыкновенные проценты с точным числом дней ссуды (360/365)

Обыкновенные проценты с приближенным числом дней ссуды (360/360)

Переменные ставки

В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки. Если это простые ставки, то наращенная на конец срока сумма определяется следующим образом:

Источник

Простые и сложные проценты по вкладам

Выгода банковского вклада оценивается не только по процентной ставке. Большое влияние на доходность депозита оказывает способ начисления процентов. В финансовой сфере существует понятие простого и сложного процента. Когда применяется тот или иной метод расчета? Как осуществляется начисление процентов по каждому способу? И какой метод выгоднее для вкладчика?

Понятие простых процентов и как они рассчитываются

Метод расчета простых процентов основан на принципе наращения денег по арифметической прогрессии. Допустим, инвестор в начале года положил в банк депозит на сумму 100 000 руб. под 10% годовых:

Поскольку банки указывают ставку за год, то чтобы определить доход за другой период (к примеру, 3 месяца), применяя простую ставку процентов, формула будет такой:

S – сумма насчитанных процентов (руб.);

P – начальная сумма вложенных средств;

I – процентная ставка за год;

Т – срок действия вклада в днях;

K – число дней в году.

То есть при вкладе 100 000 руб. на 3 месяца под 10% годовых вычисление простых процентов будет выполняться так:

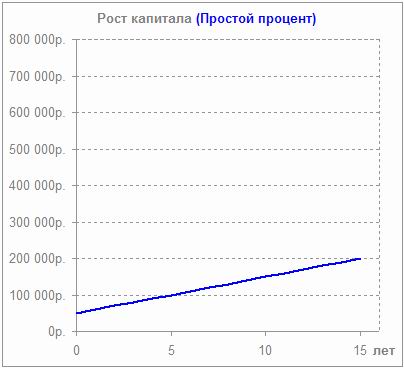
(100 000 х 10 х 92 / 365) / 100 = 2520,55 (руб.).

Получается, что в конце срока вкладчик получит на руки внесенные 100 000 руб. плюс 2520,55 руб. дохода, т.е. 102 520,55 руб.

Как рассчитать сложный процент по вкладу

В отличие от простой ставки процентов, сложная начисляется на постоянно растущую основу с учетом процентов, которые начислены за предыдущие периоды. Иными словами проценты, полученные за определенный период (неделю, месяц, квартал год) прибавляются к начальной сумме вклада (капитализируются). А в следующем периоде они начисляются уже на всю эту сумму вместе, и так каждую неделю, месяц или квартал.

Выходит, что в отличие от модели простых процентов, основа для начисления сложных будет расти с каждым новым периодом. Ведь главная суть расчетов состоит в том, что выполняется начисление процентов на процент.

Если метод простых процентов основывается на арифметической прогрессии, то сложных – на геометрической. Формула их расчета выглядит таким образом:

S – сумма насчитанных процентов (руб.);

P – начальная сумма вложенных денег;

I – процентная ставка за год;

J – период, за который проводится капитализация (дней);

K – число дней в году.

Например, при первоначальном вкладе 100 000 руб. под 10% с учетом ежемесячной капитализации за первый месяц (допустим, март) вкладчик получит:

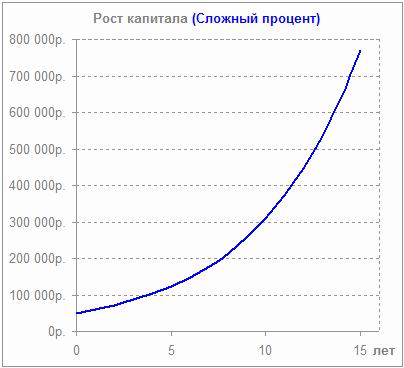
Чтобы увидеть эффект метода сложных процентов, нужно сравнить полученную сумму (102 541,79 руб.) с суммой, определенной путем расчета простых процентов (102 520,55 руб.) при тех же условиях (100 000 руб. под 10% на 3 месяца).

Получается, что во втором случае величина прибыли немного больше. При этом существует прямая зависимость: чем больше срок вклада, тем больше разница в доходах, рассчитанных разными способами.

В каких случаях используется начисление простых и сложных процентов?

Формула простых процентов по вкладам применяется, когда полученные проценты плюсуются к телу депозита лишь в конце периода или совсем не прибавляются, а переводятся на другой счет. Формулу сложных процентов используют, когда проценты насчитываются через равные временные промежутки (месяц, квартал, год). Это означает проведение капитализации процентов (когда проценты насчитываются на проценты).

Простые проценты используются в случаях оформления краткосрочных вкладов, период действия которых, в основном, меньше года. Метод сложных процентов применяется при долгосрочных вкладах, которые открываются на срок больше года.

Сравнение методов сложных и простых процентов

Хранение денег в банке с целью увеличения собственных накоплений называется наращением. Даже при самом упрощенном примере начисление процентов происходит один раз в год. Поэтому через год вкладчик закрывает депозит и забирает всю сумму плюс начисленные проценты.

Наращение по простым процентам определяется согласно формуле:

S = P (1 + ni), где:

P – начальная сумма вложенных денег;

n – количество этапов начисления процентов;

i – процентная ставка.

Величина (1 + ni) на языке финансистов называется множитель наращения простых процентов. Она показывает, во сколько раз наращенная сумма превышает изначальную.

Наращенную величину можно также представить в виде суммы:

P – первоначальная сумма вложенных денег;

I = Pni – сумма процентов.

Пример. Положив депозит в сумме 200 000 руб. под 12% годовых на полгода, клиент получает такую сумму процентов:

I = Pni = 200 000х0,5х0,12 = 12 000 (руб.);

и наращенную величину:

S = P+ I = 200 000+12 000 = 212 000 (руб.).

Величина, обратная наращению, называется дисконтирование по простым процентам. Она определяет сегодняшнюю стоимость будущей денежной суммы. Этот показатель дает возможность определить, сколько сегодня будут стоить средства, которые получит вкладчик в будущем.

Ставка дисконтирования, которая используется в расчетах, учитывает такие риски, как инфляция, изменение ставки или нормы доходности. У банков, имеющих высокую степень надежности, таких, как Сбербанк, ставка дисконтирования находится в пределах процентной ставки.

В отличие от начисления простых процентов, формула наращения по сложным процентам представляется так:

P – первоначальная сумма вложенных денег;

i – процентная ставка;

ny – количество циклов капитализации на протяжении года;

nd– количество циклов капитализации за все время депозита.

Пример. При вложении 200 000 руб. с ежеквартальной капитализацией на полгода наращенная сумма вклада составит:

S = P (1 + i/ny) nd = 200 000 (1+0,12/4) 2 = 200 000х1,03 2 = 200 000х1,0609 = 212 180 (руб.).

Если этот же пример рассчитать с учетом ежемесячной капитализации, получится:

S = P (1 + i/ny) nd = 200 000 (1+0,12/12) 6 = 200 000х1,01 6 = 200 000х1,0615 = 212 300 (руб.).

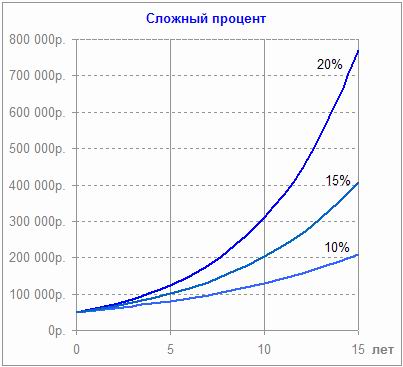
Простая и сложная ставка процентов: какие вклады выгоднее?

Из описанных примеров становится понятно: чем больше множитель наращения, на который будет умножаться сумма депозита, тем больше получится наращенный доход по вкладу.

Чтобы более наглядно продемонстрировать разницу по использованию простой схемы начисления процентов и сложной, данные занесены в таблицу:

При подсчете коэффициентов использовалась ежегодная капитализация процентов. Из таблицы видно, что:

Составив аналогичную таблицу с учетом проведения ежеквартальной капитализации, можно увидеть, что доход будет одинаков при вкладе на квартал. При более коротких депозитах (на месяц или два) больший доход будет получаться по простым процентам. При вкладах на срок более квартала, наоборот, выгоднее будут сложные проценты.

Этот принцип определения доходности вклада зависимо от метода вычисления процентов сохраняется и при расчетах на месяц. Подведя итог, можно сказать, что применение сложного процента выгодно, если период вклада превышает период капитализации. Иначе говоря:

Если срок депозита меньше, чем периодичность проведения капитализации, то расчет простых процентов по вкладам получится выгоднее.

Источник