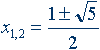что такое пропорции в живописи и архитектуре
Пропорции
Литература: Н. Врунов, Пропорции античной и средневековой архитектуры, (М., 1936); М. Гика, Эстетика пропорций в природе и искусстве, (пер. с франц.), М., 1936; Э. Мессель, Пропорции в античности и в средние века., пер. с нем., М., 1936; Graf H., Bibliographie zum Problem der Proportionen, Speyer, 1958.
Смотреть что такое «Пропорции» в других словарях:
пропорции — 3.41 пропорции: Соотношение геометрических параметров бриллианта, определяемых отношением размеров его основных элементов к среднему диаметру или ширине (для бриллиантов фантазийных форм), выраженное в процентах или числовым значением.… … Словарь-справочник терминов нормативно-технической документации
ПРОПОРЦИИ — (от лат. proportio соотношение, соразмерность) в архитектуре соразмерность элементов, система отношений частей здания, сооружения и т. п. между собой и с целым, придающие ему гармонич. целостность и художеств. завершённость. П. возникают как… … Большой энциклопедический политехнический словарь
Пропорции — (от лат. proportio соотношение, соразмерность) термин худож. практики, к рым определяется соотношение величин эл тов худож. произв., а также отд. эл тов и всего произв. в целом. Понятие П. применяется как к изображению, так и к натуре. Различают… … Российский гуманитарный энциклопедический словарь
Пропорции общественного производства — соотнесение материально вещественных элементов производства и рабочей силы, а также отраслей производства и частей совокупного общественного продукта в процессе воспроизводства. Выделяют следующие пропорции: между сферой материального… … Финансовый словарь
ПРОПОРЦИИ ОБЩЕСТВЕННОГО ПРОИЗВОДСТВА — (от лат. proportio соотношение, соразмерность) англ. proportions of public/social production; нем. Proportionen der gesellschaftlichen Produktion. Соотнесение материально вещественных элементов производства и рабочей силы, а также отраслей… … Энциклопедия социологии
ПРОПОРЦИИ ТЕЛА ЧЕЛОВЕКА — (от лат. proportio соразмерность, соотношение), соотношения размеров отдельных частей тела (туловища, конечностей и их сегментов и др.). Как правило, размеры отд. частей тела рассматриваются в соотношении с ростом (длиной тела) в целом, либо по… … Биологический энциклопедический словарь
пропорции шрифта — (Proportion) Отношение ширины [расстояние от крайней левой до крайней правой точки] и высоты знаков шрифта. Измеряется, как правило, по внешним контурам основных штрихов [доминирующий вертикальный или наклонный штрих] знака «Н». Изменения… … Шрифтовая терминология
пропорции архитектурные — Средство архитектурной композиции, заключающееся в закономерном соотношении размеров архитектурных форм и их частей [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики архитектура, основные понятия EN… … Справочник технического переводчика
пропорции издания — Соотношение размеров ширины высоты и толщины издания, устанавливаемое в зависимости от функциональных особенностей издания и художественного стиля времени. [ГОСТ Р 7.0.3 2006] Тематики издания, основные виды и элементы Обобщающие термины… … Справочник технического переводчика
Пропорции тела — Телосложение размеры, формы, пропорции и особенности частей тела, а также особенности развития костной, жировой и мышечной тканей. Размеры и формы тела каждого человека генетически запрограммированы. Эта наследственная программа реализуется в… … Википедия
10 СРЕДСТВА ГАРМОНИЗАЦИИ ФОРМЫ: ПРОПОРЦИИ
Время чтения: 7 минут
10.1 Понятие о пропорции в архитектуре
Одним из важнейших методов построения выразительной и целостной архитектурной формы является пропорционирование.
Пропорция (лат. proportio) – соразмерность, определённое соотношение частей между собой. В современной литературе понятие пропорции употребляется в трёх основных значениях:
1. Наиболее близкое к понятию соразмерности. Означает соотношение основных параметров формы (длина, ширина, высота). Именно это значение имеют в виду, когда говорят о пропорциях какого-либо здания, сооружения. Пропорция здесь характеризует объект как целое, составляет основу его образа.
2. Под пропорцией в архитектуре (также, как и математике) понимают равенство отношений количественной меры одних и тех же объективных свойств в сопоставляемых формах или их частях. В математической форме записывают как а/в = c/d. Это значение понятия «пропорция» используется в большинстве работ, посвящённых пропорционированию в архитектуре. Из математической записи такого понимания следует, что здесь в основе образования целостной формы лежит принцип геометрического подобия. Наиболее распространённым в архитектуре примером применения пропорции как равенства математических отношений является образование формы на основе подобных прямоугольников, диагонали которых либо параллельны (прямая пропорция), либо перпендикулярны (обратная пропорция) (рис. 33).
Рисунок 33 – Виды пропорций на основе подобных прямоугольников
Пропорцию, средние члены которой равны между собой, называют непрерывной. Примером непрерывной пропорции может служить ряд подобных прямоугольников, в котором длина предыдущего прямоугольника равна ширине последующего.
3. Под пропорцией в архитектуре понимают любую закономерность в соотношениях величин, которая связывает отдельные части и параметры формы в единое целое (наиболее правильное определение). Таким образом, пропорция в архитектуре есть понятие, отражающее однородность (закономерность) изменений количественной меры при переходах от одной части формы к другой и к форме в целом.
Первое и второе определения пропорции являются частными случаями последнего определения.
10.2 Виды пропорциональных отношений
В теории и практике архитектуры хорошо известны такие виды закономерных (однородных) изменений величин, как арифметическая, гармоническая и геометрическая прогрессии.
Арифметическая прогрессия выражается рядом чисел, в котором каждое последующее число больше предыдущего на одну и ту же величину. Простейшим примером арифметической прогрессии является ряд натуральных чисел 0, 1, 2, 3, 4, 5 и т. д.
Гармоническая прогрессия – это ряд чисел, обратных ряду чисел арифметической прогрессии, например: 1/2, 1/3, 1/4, 1/5, 1/6, 1/7. Отношения между соседними членами гармонического ряда по мере его возрастания также, как и в арифметической прогрессии, изменяются от контрастных к нюансным.

Рисунок 34 – Линейная и двухмерная интерпретация ряда Фибоначчи:
а – двухмерная – прямоугольники, начиная с 8:13, 13:21, приобретают пропорции «золотого сечения» и взаимное подобие – их диагонали параллельны и взаимоперпендикулярны; б – линейная – стабилизация пропорций «золотого сечения», начиная от 3:5:8;
10.3 Понятие золотого сечения
Термин «золотое сечение» был введён Леонардо да Винчи для известного деления отрезка в так называемом «крайнем и среднем отношении», при котором большая его часть является средней пропорциональной между всем отрезком и меньшей частью (рис. 36).
Золотое сечение использовал в своём творчестве И. В. Жолтовский, а Ле Корбюзье положил его в основу своего «Модулора».
Золотое сечение выражают обычно числом 1,618 или обратным ему числом 0,618. По предложению Т. Куба и М. Бара для них приняты символы Ф и 1/Ф. Золотое сечение – это единственная геометрическая прогрессия, обладающая признаком аддитивного ряда (Ф3 = Ф1 + Ф2).
Рисунок 35 – Модулор Ле Корбюзье
Рисунок 36 – Деление отрезка по золотому сечению
10.4 Пропорционирование
Пропорционирование как метод количественного согласования частей и целого имеет в своей основе геометрическую или числовую закономерность, которая способствует достижению эстетической целостности, гармоничности объёмно-пространственной формы за счёт объединения её размеров в какую-либо систему.
Особенности пропорциональных систем тесно связаны со способами строительства и измерения, которые применялись архитекторами той или иной эпохи. В древности пропорциональные системы получали путём относительно простых геометрических построений на основе треугольника, квадрата, прямоугольника или круга (рис. 36).
В Древнем Египте широко использовалась система пропорционирования на основе «священного египетского треугольника» с соотношением сторон 3:4:5, позволяющего получать прямой угол со сторонами, выраженными в простых целых числах.
Рисунок 37 – Системы пропорционирования на основе гномонических построений по принципу геометрического подобия:
1, 2 – взаимовписанные квадраты и разносторонние треугольники; 3 – «свёрнутый» ряд прямоугольников «золотого сечения» (АБВГ, ГДЕВ, ЕЖЗИ. …);
4 – равнобедренный треугольник АБВ, в котором основание и сторона находятся в отношении «золотого сечения», на его основе строится пентаграмма;
5 – пропорции на основе соотношения стороны и диагонали квадрата 1 : √2; 6 – принцип подобия прямоугольников на основе параллельности и перпендикулярности диагоналей
Перечисленные системы пропорционирования являются геометрическими, в числовом выражении они менее удобны в использовании, так как включают иррациональные числа. Однако существуют пропорциональные системы, основанные на числовых (арифметических) приёмах согласования частей и целого; это так называемые модульные системы. Простейшим примером модульной системы является масштабная сетка, в которую вписываются как общий абрис, так и детали сооружения. Модульная система пропорционирования предполагает существование модуля – условной единицы измерения. Применяемая в нашей стране модульная система (ЕМС) также использует единый модуль (М = 100 см), на основе которого путём его членения или умножения получают все принятые в строительстве размеры.
Пропорционирование может быть использовано в двух основных направлениях: как метод создания целостной формы и как метод выявления закономерностей построения уже созданных архитектурных форм. При этом следует понимать, что закономерности, выявленные в уже созданных архитектурных формах, далеко не всегда осознанно применялись их создателями.
Пропорционирование – достаточно сильное, но далеко не единственное средство гармонизации архитектурной формы, и поэтому одно только совершенство пропорции ещё не является гарантом получения совершенного архитектурного произведения.
Рисунок 40 – Примеры студенческих работ (1 курс):
1 – пропорционирование (ряд Фибоначчи);
2 – пропорционирование на основе пентаграммы
LiveInternetLiveInternet
—Музыка
—Рубрики
—Поиск по дневнику
—Интересы
—Друзья
—Постоянные читатели
—Статистика
Золотое сечение в живописи, математике, архитектуре, искусстве.
Золотое сечение – гармоническая пропорция
В математике пропорцией (лат. proportio) называют равенство двух отношений: a : b= c : d.
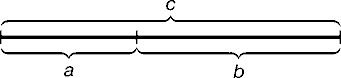
Отрезок прямой АВ можно разделить на две части следующими способами:
— на две равные части – АВ : АС= АВ : ВС;
— на две неравные части в любом отношении (такие части пропорции не образуют);
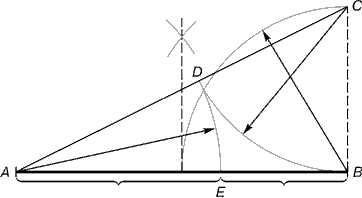
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
Рис. 2. Деление отрезка прямой по золотому сечению. BC= 1/2 AB; CD= BC
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась “О перспективе в живописи”. Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли “Божественная пропорция” с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее “божественную суть” как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. “Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать”.
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя “Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности”.
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M.
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы “вместе с водой выплеснули и ребенка”. Вновь “открыто” золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд “Эстетические исследования”. С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях “математической эстетикой”.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название “Золотое деление как основной морфологический закон в природе и искусстве”. В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.
Ряд Фибоначчи
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд “Книга об абаке” (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила “Сколько пар кроликов в один год от одной пары родится”. Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, и т.д.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3= 5; 3 + 5= 8; 5 + 8= 13, 8 + 13= 21; 13 + 21= 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34= 0,617, а 34 : 55= 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.
Обобщенное золотое сечение
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта. Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал. Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений.
Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же “двоичный” ряд гирь 1, 2, 4, 8, 16. на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2= 1 + 1; 4= 2 + 2. во втором – это сумма двух предыдущих чисел 2= 1 + 1, 3= 2 + 1, 5= 3 + 2. Нельзя ли отыскать общую математическую формулу, из которой получаются и “двоичный” ряд, и ряд Фибоначчи? А может быть, эта формула даст нам новые числовые множества, обладающие какими-то новыми уникальными свойствами?
Очевидно, что при S= 0 из этой формулы мы получим “двоичный” ряд, при S= 1 – ряд Фибоначчи, при S= 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1 – xS – 1= 0.
Нетрудно показать, что при S= 0 получается деление отрезка пополам, а при S = 1 –знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! Математики в таких случаях говорят, что золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
Факты, подтверждающие существование золотых S-сечений в природе, приводит белорусский ученый Э.М. Сороко в книге “Структурная гармония систем” (Минск, “Наука и техника”, 1984). Оказывается, например, что хорошо изученные двойные сплавы обладают особыми, ярко выраженными функциональными свойствами (устойчивы в термическом отношении, тверды, износостойки, устойчивы к окислению и т. п) только в том случае, если удельные веса исходных компонентов связаны друг с другом одной из золотых S-пропорций. Это позволило автору выдвинуть гипотезу о том, что золотые S-сечения есть числовые инварианты самоорганизующихся систем. Будучи подтвержденной экспериментально, эта гипотеза может иметь фундаментальное значение для развития синергетики – новой области науки, изучающей процессы в самоорганизующихся системах.С помощью кодов золотой S-пропорции можно выразить любое действительное число в виде суммы степеней золотых S-пропорций с целыми коэффициентами.Принципиальное отличие такого способа кодирования чисел заключается в том, что основания новых кодов, представляющие собой золотые S-пропорции, при S> 0 оказываются иррациональными числами. Таким образом, новые системы счисления с иррациональными основаниями как бы ставят “с головы на ноги” исторически сложившуюся иерархию отношений между числами рациональными и иррациональными. Дело в том, что сначала были “открыты” числа натуральные; затем их отношения – числа рациональные. И лишь позже – после открытия пифагорейцами несоизмеримых отрезков – на свет появились иррациональные числа. Скажем, в десятичной, пятеричной, двоичной и других классических позиционных системах счисления в качестве своеобразной первоосновы были выбраны натуральные числа – 10, 5, 2, – из которых уже по определенным правилам конструировались все другие натуральные, а также рациональные и иррациональные числа.Своего рода альтернативой существующим способам счисления выступает новая, иррациональная система, в качестве первоосновы, начала счисления которой выбрано иррациональное число (являющееся, напомним, корнем уравнения золотого сечения); через него уже выражаются другие действительные числа.В такой системе счисления любое натуральное число всегда представимо в виде конечной, – а не бесконечной, как думали ранее! – суммы степеней любой из золотых S-пропорций. Это одна из причин, почему “иррациональная” арифметика, обладая удивительной математической простотой и изяществом, как бы вобрала в себя лучшие качества классической двоичной и “Фибоначчиевой” арифметик.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.
Другим примером из архитектуры древности является Пантеон.
Известный русский архитектор М. Казаков в своем творчестве широко использовал “золотое сечение”.
Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова (Ленинский проспект, д. 5).
Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова.
Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г.
При восстановлении здание приобрело более массивные формы. Не сохранилась и внутренняя планировка здания, о которой дают представления только чертеж нижнего этажа.
Многие высказывания зодчего заслуживают внимание и в наши дни. О своем любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания. К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождем является рассудок”.
| Рубрики: | Тренинг воображения, головоломки, шахматы Познание мира и себя Технологии, изобретения, |
Метки: золотое сечение
Процитировано 2 раз
Понравилось: 3 пользователям