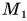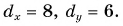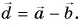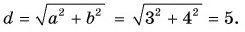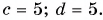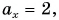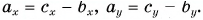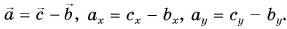что такое проекция вектора на ось
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Как определяют проекцию вектора на ось
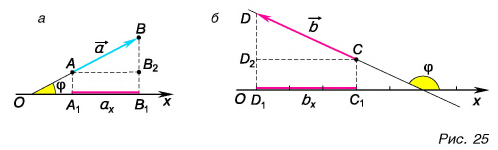
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 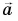
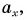
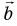
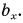
Проекция 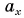
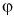
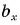
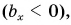
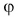
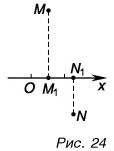
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 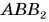
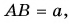
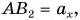
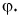
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
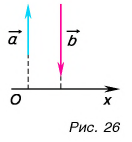
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
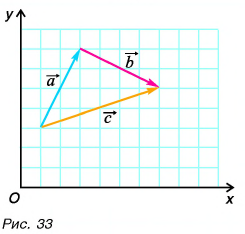
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 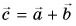
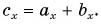
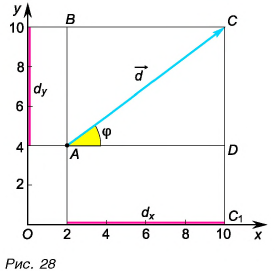
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
Рассмотрим вектор 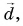
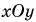
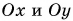
Модуль вектора 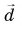
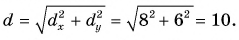
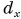
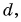
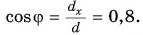
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
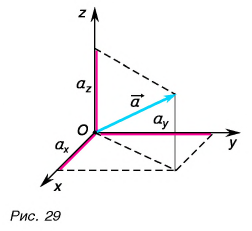
Вектор в пространстве определяется тремя проекциями: 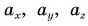
Главные выводы:
Пример №1
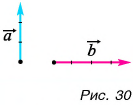
1. Определите сумму и разность взаимно перпендикулярных векторов 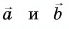
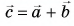
Решение
Сумму векторов 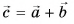
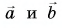
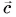
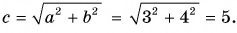
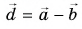
Модуль вектора 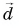
Ответ:
Пример №2
Выразите вектор 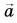
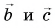
Решение
По правилу треугольника находим: 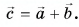
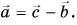
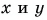
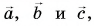
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Вектор. Проекция вектора на ось.
Проекцию вектора на ось ОХ принято понимать в различных смысловых значениях: геометрическом и арифметическом (алгебраическом).
На письме геометрическую проекцию данного вектора можно показать следующим образом:
или
.
В случае задачи оси ОХ с помощью вектора с, вектор называется проекцией вектора
на направление вектора с, и на письме его принято обозначать в виде
.
Геометрическую проекцию вектора на ось ОХ иначе принято называть компонентой вектора по оси ОХ.
2. Алгебраической или арифметической проекцией вектора на ось ОХ (или на направление вектора с) называется длина вектора
, которая берется с положительным «+» или с отрицательным «-» знаком, согласно тому, направлен ли рассматриваемый вектор одинаково с осью ОХ или иначе.
На письме обозначается следующим образом:
или
.
Геометрическая проекция вектора выражена в виде вектора, а алгебраическая проекция вектора представлена числовым значением.
В случае, когда векторы и
равны, их алгебраические проекции по одинаковой оси тоже равны между собой
Аналогично можно выразить случай с геометрической проекцией вектора.
Арифметическая проекция одного и того же вектора, но для случая разнонаправленных осей, (О1Х1 и О2Х2) равна:
.
Аналогично получаем и для случая геометрической проекции векторов, но только при условии параллельности осей, которые нам заданы.
3. Рассмотрим взаимосвязь между компонентой (геометрической проекцией) и алгебраической проекцией вектора.
При условии когда c1 является разнонаправленным с осью ОХ вектором, и имеет длину равную 1, геометрическая проекция выбранного вектора а по оси ОХ равна произведению вектора с1 на алгебраическую проекцию вектора а по оси ОХ. Сказанное записывают в виде:
.
В случае параллельности, но разнонаправленности осей алгебраические проекции не равны, т.к. отличаются своим знаком.
Таким образом, =-2
.
Проекция вектора на ось
Вектор может отбрасывать тень (проекцию) на какую-нибудь ось
Если:
Примечание:
Длина вектора – это положительная величина, а проекция вектора может быть отрицательной
Как разложить вектор на проекции
Мы уже находили длину и направление вектора по его координатам.
Теперь решим обратную задачу: пользуясь длиной и направлением вектора, найдем его координаты.
На плоскости (две оси) легко разложить вектор на проекции, если известны:
Алгоритм действий для разложения вектора на проекции
Важно! Вектор, который мы раскладываем, всегда является гипотенузой.
Формулы разложения вектора на проекции
Формулы разложения легко запомнить с помощью фразы:
Гипотенузу умножаем на косинус (угла), получаем катет, который касается (дуги).
На языке математики эта фраза запишется так:
\[ |\vec
Катет \( m_
Если длину вектора умножим на синус, то получим второй катет:
\[ |\vec
Катет \( m_
Обе формулы запишем в виде системы:
\[ \large \boxed <\begin
Величина \( |\vec
Что такое проекция вектора на ось
1. Какая величина называется векторной (или просто вектором)?
Физическая величина, которая характеризуется не только числовым значением (модулем), но и направлением, называется векторной величиной (или просто вектором).
Для векторной величины одинаково важны числовое значение (модуль) и направление.
Примеры векторных величин:
— скорость,
— перемещение,
— сила.
2. Какая величина называются скалярной (или просто скаляром)?
Величины, которые не имеют направления и задаются только числом, называются скалярными величинами или скалярами.
Примеры скалярных величин:
3. Как изображают векторную величину?
Векторную величину изображают в виде стрелки, которая начинается в некоторой точке и заканчивается острием, указывающим направление..
Такой отрезок-стрелка называется вектором.
Длина стрелки в выбранном масштабе выражает модуль векторной величины.
Векторы обозначают буквами со стрелкой над ними.
Такой же буквой, но без стрелки обозначают модуль вектора.
4. Если два вектора равны друг другу по модулю, но направления векторов различны, то можно ли сказать, что эти векторы равны друг другу?
Нет, нельзя.
Равными считаются векторы, у которых одинаковы и модули, и направления.
5. Чем отличается векториая величина от скалярной?
Проекция вектора на координатную ось
1. Как построить проекцию вектора на координатную ось?

Есть вектор а.
Опустим из точки А (начало вектора) и точки В (конец вектора) перпендикуляры на ось ОX.
Получим на оси точки ха и хв — это проекции точек А и В на ось ОX.
Длину отрезка ха-хв между проекциями начала и конца вектора называют проекцией вектора а на ось ОX и обозначают, как ах.
Проекцию вектора на ось обозначают той же буквой, что и вектор, но без стрелки и с индексом оси.
Проекция вектора — величина скалярная.
2. Если вектор перемещения параллелен координатной оси, то чему равен модуль проекции вектора на эту ось?
Если вектор параллелен оси координат, то модуль его проекции ( |ax| ) равен модулю ( a ) самого вектора.
3. Что называют проекцией вектора на координатную ось?
Длину отрезка на координатной оси между проекциями начала и конца вектора, взятую со знаком « + » или « —», называют проекцией вектора а на координатную ось.
Проекция вектора на координатную ось может быть, как положительной, так и отрицательной.
Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью.
Проекция вектора на ось считается отрицательной, если вектор направлен противоположно оси.
Если вектор перпендикулярен координатной оси, то при любом направлении вектора его проекция на ось равна нулю.
Что такое проекция вектора на ось
Сформулируем ряд базовых определений.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
то есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора 

Пусть в трехмерном пространстве заданы векторы 
1. Сложение двух векторов производится покоординатно, то есть если
Геометрически два вектора складываются по двум правилам:
а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;
б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.
Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.
При λ>0 – вектор 





4. Пусть в пространстве задана направленная прямая (ось l ), вектор 
Рассмотрим некоторые основные свойства проекций:
1) проекция вектора 


2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;
3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.
5. Скалярным произведением 


Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть
Отсюда следует условие перпендикулярности ненулевых векторов 

С помощью скалярного произведения векторов находят работу постоянной силы 
Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?
Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix
Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала
Угол φ между 

– 


– векторы 
Примечание. Определитель (2.25) раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны
Следствие 3. Векторный квадрат любого вектора равен нулю
Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.
— перпендикулярен плоскости, проходящей через точки O , A , B ;
Следовательно, момент силы 

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).
Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
Объем треугольной пирамиды, построенной на этих же векторах, равен
Решение. Найдем координаты векторов
По формуле (2.36) объем пирамиды, построенной на векторах 

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.
получим выражение вектора 
Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все
Базисом n – мерного пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.