что такое проекция катета на гипотенузу
Узнать ещё
Знание — сила. Познавательная информация
Пропорциональные отрезки в прямоугольном треугольнике
Запомнить соотношения, связывающие пропорциональные отрезки в прямоугольном треугольнике, помогает цветовая ассоциация.
Высота прямоугольного треугольника, проведенная к гипотенузе, делит ее на отрезки, которые называются проекциями катетов на гипотенузу.
Свойства прямоугольного треугольника:
1. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
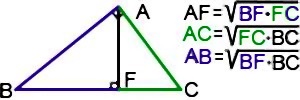
Например, в треугольнике ABC AF — высота, проведенная к гипотенузе BC, BF — проекция катета AB на гипотенузу, FC — проекция катета AC на гипотенузу.
Если выделить каждую пару — катет и его проекция на гипотенузу — одним цветом, запомнить пропорциональные отрезки в прямоугольном треугольнике можно быстро и легко.
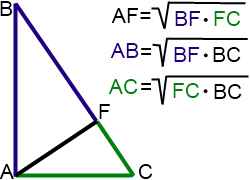
Как бы ни был расположен на чертеже прямоугольный треугольник, цветовая ассоциация поможет найти пропорциональные отрезки и правильно составить связывающие их соотношения:
Выделить пропорциональные отрезки цветами можно на черновике. При решении задачи, в которой прямоугольный треугольник — только один из элементов чертежа, достаточно для нахождения связи между пропорциональными отрезками на черновике изобразить отдельный фрагмент с этим треугольником.
Что такое проекция катета на гипотенузу
Основные метрические сооьтношения в прямоугольном треугольнике
§1. Прямоугольный треугольник. Метрические соотношения.
Основные метрические сооьтношения в прямоугольном треугольнике
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
Прямоугольные треугольники
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
Площадь прямоугольного треугольника равна половине произведения его катетов
Подставим найденное значение в формулу косинуса
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
Как найти проекцию катета на гипотенузу
Если в исходных условиях задачи приведены длины гипотенузы (С) и того катета (А), проекцию которого (Ас) требуется вычислить, то используйте одно из свойств треугольника. Воспользуйтесь тем, что среднее геометрическое длин гипотенузы и искомой проекции равно длине катета: А = √(С*Ас). Так как понятие «среднее геометрическое» эквивалентно «корню из произведения», то для нахождения проекции катета возводите в квадрат длину катета и делите полученное значение на длину гипотенузы: Ас = (А/√С)² = А²/С.
Если длина гипотенузы неизвестна, а даны лишь длины обоих катетов (А и В), то в вычислении длины нужной проекции (Ас) можно задействовать теорему Пифагора. Выразите в соответствии с ней длину гипотенузы через длины катетов √(А²+В²) и подставьте полученное выражение в формулу из предыдущего шага: Ас = А²/√(А²+В²).
Если длины катетов неизвестны, но дано их соотношение (x/y), а также длина гипотенузы (C), то воспользуйтесь парой формул из первого и третьего шагов. Согласно выражению из первого шага, соотношение проекций катетов (Ас и Вс) будет равно соотношению квадратов их длин: Ас/Вс = x²/y². С другой стороны, согласно формуле из предыдущего шага, Ас+Вс = С. В первом равенстве выразите длину ненужной проекции через нужную и подставьте полученное значение во вторую формулу: Ас + Ас*x²/y² = Ас*(1 + x²/y²) = С. Из этого равенства выведите формулу нахождения нужной проекции катета: Ас = С/(1 + x²/y²).
Если известна длина проекции на гипотенузу одного катета (Вс), а длина самой гипотенузы не приведена в условиях, но дана высота (Н), проведенная из прямого угла треугольника, то этого тоже будет достаточно для вычисления длины проекции другого катета (Ас). Возведите высоту в квадрат и разделите на длину известной проекции: Ас = Н²/Вс.