что такое приведенная система вычетов
Приведённая система вычетов
Смотреть что такое «Приведённая система вычетов» в других словарях:
Приведённая система вычетов — часть полной системы вычетов (См. Полная система вычетов), состоящая из чисел взаимно простых с модулем m. П. с. в. содержит φ(m) чисел [φ(m) число чисел, взаимно простых с m и меньших m]. Всякие φ(m) чисел, не сравнимые по модулю m и… … Большая советская энциклопедия
Приведенная система вычетов — Приведённая система вычетов по модулю m набор, составленный из всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(m) функция Эйлера. В качестве приведённой… … Википедия
Мультипликативная группа кольца вычетов — Приведённая система вычетов по модулю m множество всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(·) функция Эйлера. В качестве приведённой системы вычетов… … Википедия
Функция Эйлера — Не следует путать с функцией распределения простых чисел. Первая тысяча значений Функция Эйлера φ(n) мультипликативная … Википедия
Сравнение по модулю — Сравнение[1] по модулю натурального числа n в теории чисел отношение эквивалентности на кольце целых чисел, связанное с делимостью на n. Факторкольцо по этому отношению называется кольцом вычетов. Совокупность соответствующих тождеств и… … Википедия
Конечная группа — Симметрия снежинки связана с группой поворотов на угол, кратный 60° Конечная группа алгебраическая группа, содержащая конечное число элементов (это число называется её порядком). Далее группа предполагается мультипликативной, то есть операция в… … Википедия
Четверная группа Клейна — Четверная группа Клейна группа четвёртого порядка, играет важную роль в высшей алгебре. Содержание 1 Определение 2 Обозначение 3 … Википедия
Кризис — (Krisis) Содержание Содержание Финансовый кризис История Мировая история 1929 1933 годы время Великой депрессии Черный понедельник 1987 года. В 1994 1995 годах произошел Мексиканский кризис В 1997 году Азиатский кризис В 1998 году Российский… … Энциклопедия инвестора
Российская империя — Координаты: 58° с. ш. 70° в. д. / 58° с. ш. 70° в. д. … Википедия
Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия
Приведенная система вычетов
Согласно свойству сравнений №15, числа одного и того же класса по модулю m имеют с модулем m один и тот же НОД. Особенно важны классы, для которых он равен 1.
Взяв от каждого из таких классов по одному числу, получим приведенную систему вычетов по модулю m. Обычно ее выделяют из системы наименьших неотрицательных вычетов по модулю m.
Приведенная система наименьших неотрицательных вычетов по модулю m обозначается Um.
Количество чисел в приведенной системе вычетов по модулю m, очевидно, равно φ(m).
Приведенная система вычетов по модулю 15 есть <1; 2; 4; 7; 8; 11; 13; 14>. Заметим, что φ(15)=(5–1)∙(3–1)= 8 и действительно, в приведенной системе вычетов по модулю 15 ровно 8 элементов.
Утверждение 1
Любые φ(m) чисел, попарно несравнимых по модулю m и взаимно простых с m, образуют приведенную систему вычетов.
(Доказательство очевидно как в утверждении 1 пункт 2)
Утверждение 2
Обратный элемент.
Говорят, что элемент b называется обратным к a по модулю m, если a∙b≡1(mod m), и пишут b ≡ a –1 (mod m).
Вообще, классическая теория чисел не нуждается в таком понятии как обратный элемент, в чем можно убедиться, ознакомившись, например, с [5]. Однако криптология использует системы вычетов как в теоретико-числовом, так и в алгебраическом аспекте, а потому, для удобства изложения алгебраических основ криптологии, мы вводим понятие обратного элемента.
Возникает вопрос – для всех ли элементов по данному модулю m существует обратный (по умножению), и если для каких-то элементов обратный существует, как его найти?
Для ответа на этот вопрос воспользуемся расширенным алгоритмом Евклида. Рассмотрим сначала взаимно простые число a и модуль m. Тогда, очевидно, (a,m)=1. Расширенный алгоритм Евклида позволяет получить числа x и y, такие, что ax+my=(a,m), или, что то же самое, ax+my=1. Из последнего выражения получаем сравнение ax+my≡1(mod m). Поскольку my≡0(mod m), то ax≡1(mod m), а значит полученное с помощью расширенного алгоритма Евклида число x как раз и есть искомый обратный элемент к числу a по модулю m.
Воспользуемся расширенным алгоритмом Евклида.
Проверка: 5∙3=15. 15≡1(mod 7).
Действительно, 3 является обратным элементом к 5 по модулю 7.
Итак, конструктивным образом убедились в том, что для чисел, взаимно простых с модулем, существует обратный по этому модулю. А существуют ли обратные элементы для чисел, не являющихся с модулем взаимно простыми?
Пусть (a,m)=d≠1. Тогда a и m представимы в виде a=d∙a1, m=d∙m1. Допустим, что для a существует обратный элемент по модулю m, то есть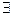 
b: a∙b≡1(modm). Тогда a∙b= m∙k +1. Или, что то же самое, d∙a1∙b= d∙m1∙k +1. Но тогда по теореме 2 из §1 п.1, в силу того, что и левая часть данного уравнения, и первое слагаемое в правой части делятся на d, то d\1, а это не так, поскольку d≠1. Пришли к противоречию, следовательно предположение о существовании обратного элемента неверно.
Итак, мы только что доказали
Теорему обратимости
Суммируя все рассуждения этого пункта, можем сказать, что обратимыми являются только взаимно простые с модулем числа, и найти обратные для них можно с помощью расширенного алгоритма Евклида.
Приведённая система вычетов
Смотреть что такое «Приведённая система вычетов» в других словарях:
Приведённая система вычетов — по модулю m набор, составленный из всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(m) функция Эйлера. В качестве приведённой системы вычетов по модулю m… … Википедия
Приведенная система вычетов — Приведённая система вычетов по модулю m набор, составленный из всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(m) функция Эйлера. В качестве приведённой… … Википедия
Мультипликативная группа кольца вычетов — Приведённая система вычетов по модулю m множество всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(·) функция Эйлера. В качестве приведённой системы вычетов… … Википедия
Функция Эйлера — Не следует путать с функцией распределения простых чисел. Первая тысяча значений Функция Эйлера φ(n) мультипликативная … Википедия
Сравнение по модулю — Сравнение[1] по модулю натурального числа n в теории чисел отношение эквивалентности на кольце целых чисел, связанное с делимостью на n. Факторкольцо по этому отношению называется кольцом вычетов. Совокупность соответствующих тождеств и… … Википедия
Конечная группа — Симметрия снежинки связана с группой поворотов на угол, кратный 60° Конечная группа алгебраическая группа, содержащая конечное число элементов (это число называется её порядком). Далее группа предполагается мультипликативной, то есть операция в… … Википедия
Четверная группа Клейна — Четверная группа Клейна группа четвёртого порядка, играет важную роль в высшей алгебре. Содержание 1 Определение 2 Обозначение 3 … Википедия
Кризис — (Krisis) Содержание Содержание Финансовый кризис История Мировая история 1929 1933 годы время Великой депрессии Черный понедельник 1987 года. В 1994 1995 годах произошел Мексиканский кризис В 1997 году Азиатский кризис В 1998 году Российский… … Энциклопедия инвестора
Российская империя — Координаты: 58° с. ш. 70° в. д. / 58° с. ш. 70° в. д. … Википедия
Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия
Приведенная система вычетов
Смотреть что такое «Приведенная система вычетов» в других словарях:
ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ — по модулю т набор, составленный из всех чисел полной системы вычетов по модулю те, взаимно простых с т. П. с. в. по модулю тсостоит из j(т). чисел, где j(т) функция Эйлера. В качестве П. с. в. по модулю тобычно берутся взаимно простые с тчисла… … Математическая энциклопедия
Функция Эйлера — Не следует путать с функцией распределения простых чисел. Первая тысяча значений Функция Эйлера φ(n) мультипликативная … Википедия
СРАВНЕНИЕ — соотношение между целыми числами а и и вида a=b+mk, означающее, что их разность а b делится на заданное целое положительное число т, наз. модулем сравнения; при этом аназ. вычетом целого числа bпо модулю т. Для выражения сравнимости чисел аи bпо… … Математическая энциклопедия
Администрация США — (Administration of USA) Определение администрации США, высшие руководители США Определение администрации США, высшие руководители США, административные учреждения Содержание Содержание Определение Административное право Служба высших… … Энциклопедия инвестора
ЛОГИКА ВЫСКАЗЫВАНИЙ — раздел логики, в котором изучаются истинностные взаимосвязи между высказываниями. В рамках данного раздела высказывания (пропозиции, предложения) рассматриваются только с т.зр. их истинности или ложности, безотносительно к их внутренней субъектно … Философская энциклопедия
Системы вычетов
По этой ссылке вы найдёте полный курс лекций по математике:
Возможно вам будут полезны данные страницы:
Итак, числа из одного класса вычетов по модулю т имеют один и тот же наибольший обший делитель с т. Поэтому становится корректным следующее определени е. Вычет по модулю т называют приведенным, если он взаимно прост с т. Совокупность приведенных вычетов из разных классов вычетов называют приведенной системой вычетов. Пример 2.
| При m = 7 приведенная система вычетов |
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.