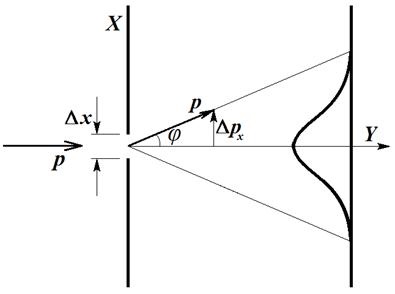
что такое принцип неопределенности
Принцип неопределенности Гейзенберга в квантовой механике
Обновлено: 19 Июня 2021
Разбираем принцип неопределенности Гейзенберга с пояснениями и примерами.
Что такое принцип неопределенности Гейзенберга
Если говорить простым языком, это фундаментальный закон квантовой механики, который гласит, что невозможно точно определить скорость и местонахождение частицы.

Источник: userapi.com
Если обратиться к Википедии, там мы увидим определение: «соотношение неопределенностей, устанавливающее предел точности одновременного определения пары характеризующих систему квантовых наблюдаемых, описываемых некоммутирующими операторами». Чем точнее можно рассмотреть одну характеристику частицы, тем хуже получится рассмотреть вторую. То есть чем точнее определяются координаты частицы, тем неопределеннее становится ее импульс. Точно так и наоборот.
В чем заключается сущность и смысл
Легче всего этот принцип можно представить с помощью примера. Представим, что электрон — это баскетбольный мяч, а фотоны — это бильярдные шары. За счет фотонов мы видим мир и расположение объектов на том или ином месте. Происходит это, когда фотоны отскакивают от объекта и попадают к нам в глаз (проще говоря, это свет).
Так вот, кидая бильярдные шары в баскетбольный мяч, мы будем следить за шарами, которые отскакивают, чтобы понять его местонахождение. Вот только шары довольно тяжелые относительно баскетбольного мяча, поэтому каждый раз будут придавать ему импульс, и тот будет отдаляться. Таким образом, чем сильнее мы пытаемся определить местоположение электрона, тем усиленнее кидаем в него фотоны и ненароком двигаем.
По принципу неопределенности Гейзенберга ни один доступный сегодня метод определения положения электрона не пройдет бесследно для импульса, и мы не сможем определить оба фактора одновременно.
Формула выглядит следующим образом:
\(ħ\) — постоянная Планка;
\(Δx\) — среднеквадратическое отклонение координаты;
\(Δp\) — среднеквадратическое отклонение импульса.
Необычные последствия соотношения неопределенностей
«Отсутствие покоя»
Это состояние с наименьшей энергией. Как вам уже известно из уроков физики, полная энергия частицы складывается из кинетической и потенциальной E=p²/2m+U⃗(r). Состояние с наиболее низким энергетически запасом соответствует нахождению частицы в минимуме потенциальной энергии с нулевым импульсом. Но это противоречит соотношению неопределенностей, так как оказываются точно заданы координата и импульс. Поэтому в квантовой задаче, в состоянии самой низкой возможной энергии, частица должна иметь «слегка» неопределенную координату и «слегка» неопределенный импульс. Легче представить это как дрожание частицы рядом с положением равновесия. Однако подобная аналогия условна, так как мы рассматриваем исключительно квантовый эффект делокализации частицы.
Нулевые колебания гармонического осциллятора
Из-за условного дрожания частицы рядом с положением равновесия делокализацию квантовой частицы в ее основном состоянии (состояние с наиболее низкой энергией) называют «нулевыми колебаниями».
При точном решении задач об уровнях гармонического осциллятора появляется еще половина кванта энергии, из-за чего уравнение выглядит следующим образом: \(E=ħ\omega(n+1/2).\)
Размах делокализации частицы в пространстве называют амплитудой нулевых колебаний. Можно ее оценить для гармонического осциллятора.
Квантовые кристаллы гелия
Очевидно, что амплитуда нулевых колебаний больше, если легче атомы. А чем она больше, тем слабее воздействие между ними. В пример можно привести кристаллы, которые формируются при экстремально низких температурах из атомов гелия. Эти атомы в четыре раза легче кислорода и очень слабо взаимодействуют друг с другом, так как являются инертными. В том случае амплитуда нулевых колебаний близка к межатомному расстоянию. Из-за такой делокализации атомов кристалл не держится: жидкий гелий не замерзает при температурах до абсолютного нуля. Чтобы стабилизировать жесткую фазу, нужно ко всему прочему приложить давление в
Остались вопросы? Ленитесь разобраться в сложной теме? Заходи на сервис ФениксХелп. Лучшие специалисты помогут решить любую задачу, написать контрольную, курсовую или дипломную работу любой сложности.
Принцип неопределенности Гейзенберга
Невозможно одновременно с точностью определить координаты и скорость квантовой частицы.
В обыденной жизни нас окружают материальные объекты, размеры которых сопоставимы с нами: машины, дома, песчинки и т. д. Наши интуитивные представления об устройстве мира формируются в результате повседневного наблюдения за поведением таких объектов. Поскольку все мы имеем за плечами прожитую жизнь, накопленный за ее годы опыт подсказывает нам, что раз всё наблюдаемое нами раз за разом ведет себя определенным образом, значит и во всей Вселенной, во всех масштабах материальные объекты должны вести себя аналогичным образом. И когда выясняется, что где-то что-то не подчиняется привычным правилам и противоречит нашим интуитивным понятиям о мире, нас это не просто удивляет, а шокирует.
В первой четверти ХХ века именно такова была реакция физиков, когда они стали исследовать поведение материи на атомном и субатомном уровнях. Появление и бурное развитие квантовой механики открыло перед нами целый мир, системное устройство которого попросту не укладывается в рамки здравого смысла и полностью противоречит нашим интуитивным представлениям. Но нужно помнить, что наша интуиция основана на опыте поведения обычных предметов соизмеримых с нами масштабов, а квантовая механика описывает вещи, которые происходят на микроскопическом и невидимом для нас уровне, — ни один человек никогда напрямую с ними не сталкивался. Если забыть об этом, мы неизбежно придем в состояние полного замешательства и недоумения. Для себя я сформулировал следующий подход к квантово-механическим эффектам: как только «внутренний голос» начинает твердить «такого не может быть!», нужно спросить себя: «А почему бы и нет? Откуда мне знать, как всё на самом деле устроено внутри атома? Разве я сам туда заглядывал?» Настроив себя подобным образом, вам будет проще воспринять статьи этой книги, посвященные квантовой механике.
Принцип Гейзенберга вообще играет в квантовой механике ключевую роль хотя бы потому, что достаточно наглядно объясняет, как и почему микромир отличается от знакомого нам материального мира. Чтобы понять этот принцип, задумайтесь для начала о том, что значит «измерить» какую бы то ни было величину. Чтобы отыскать, например, эту книгу, вы, войдя в комнату, окидываете ее взглядом, пока он не остановится на ней. На языке физики это означает, что вы провели визуальное измерение (нашли взглядом книгу) и получили результат — зафиксировали ее пространственные координаты (определили местоположение книги в комнате). На самом деле процесс измерения происходит гораздо сложнее: источник света (Солнце или лампа, например) испускает лучи, которые, пройдя некий путь в пространстве, взаимодействуют с книгой, отражаются от ее поверхности, после чего часть из них доходит до ваших глаз, проходя через хрусталик, фокусируется, попадает на сетчатку — и вы видите образ книги и определяете ее положение в пространстве. Ключ к измерению здесь — взаимодействие между светом и книгой. Так и при любом измерении, представьте себе, инструмент измерения (в данном случае, это свет) вступает во взаимодействие с объектом измерения (в данном случае, это книга).
В классической физике, построенной на ньютоновских принципах и применимой к объектам нашего обычного мира, мы привыкли игнорировать тот факт, что инструмент измерения, вступая во взаимодействие с объектом измерения, воздействует на него и изменяет его свойства, включая, собственно, измеряемые величины. Включая свет в комнате, чтобы найти книгу, вы даже не задумываетесь о том, что под воздействием возникшего давления световых лучей книга может сдвинуться со своего места, и вы узнаете ее искаженные под влиянием включенного вами света пространственные координаты. Интуиция подсказывает нам (и, в данном случае, совершенно правильно), что акт измерения не влияет на измеряемые свойства объекта измерения. А теперь задумайтесь о процессах, происходящих на субатомном уровне. Допустим, мне нужно зафиксировать пространственное местонахождение электрона. Мне по-прежнему нужен измерительный инструмент, который вступит во взаимодействие с электроном и возвратит моим детекторам сигнал с информацией о его местопребывании. И тут же возникает сложность: иных инструментов взаимодействия с электроном для определения его положения в пространстве, кроме других элементарных частиц, у меня нет. И, если предположение о том, что свет, вступая во взаимодействие с книгой, на ее пространственных координатах не сказывается, относительно взаимодействия измеряемого электрона с другим электроном или фотонами такого сказать нельзя.
В начале 1920-х годов, когда произошел бурный всплеск творческой мысли, приведший к созданию квантовой механики, эту проблему первым осознал молодой немецкий физик-теоретик Вернер Гейзенберг. Начав со сложных математических формул, описывающих мир на субатомном уровне, он постепенно пришел к удивительной по простоте формуле, дающий общее описание эффекта воздействия инструментов измерения на измеряемые объекты микромира, о котором мы только что говорили. В результате им был сформулирован принцип неопределенности, названный теперь его именем:
математическое выражение которого называется соотношением неопределенностей Гейзенберга:
где Δx — неопределенность (погрешность измерения) пространственной координаты микрочастицы, Δv — неопределенность скорости частицы, m — масса частицы, а h — постоянная Планка, названная так в честь немецкого физика Макса Планка, еще одного из основоположников квантовой механики. Постоянная Планка равняется примерно 6,626 x Дж·с, то есть содержит 33 нуля до первой значимой цифры после запятой.
Термин «неопределенность пространственной координаты» как раз и означает, что мы не знаем точного местоположения частицы. Например, если вы используете глобальную систему рекогносцировки GPS, чтобы определить местоположение этой книги, система вычислит их с точностью до 2-3 метров. (GPS, Global Positioning System — навигационная система, в которой задействованы 24 искусственных спутника Земли. Если у вас, например, на автомобиле установлен приемник GPS, то, принимая сигналы от этих спутников и сопоставляя время их задержки, система определяет ваши географические координаты на Земле с точностью до угловой секунды.) Однако, с точки зрения измерения, проведенного инструментом GPS, книга может с некоторой вероятностью находиться где угодно в пределах указанных системой нескольких квадратных метров. В таком случае мы и говорим о неопределенности пространственных координат объекта (в данном примере, книги). Ситуацию можно улучшить, если взять вместо GPS рулетку — в этом случае мы сможем утверждать, что книга находится, например, в 4 м 11 см от одной стены и в 1м 44 см от другой. Но и здесь мы ограничены в точности измерения минимальным делением шкалы рулетки (пусть это будет даже миллиметр) и погрешностями измерения и самого прибора, — и в самом лучшем случае нам удастся определить пространственное положение объекта с точностью до минимального деления шкалы. Чем более точный прибор мы будем использовать, тем точнее будут полученные нами результаты, тем ниже будет погрешность измерения и тем меньше будет неопределенность. В принципе, в нашем обыденном мире свести неопределенность к нулю и определить точные координаты книги можно.
И тут мы подходим к самому принципиальному отличию микромира от нашего повседневного физического мира. В обычном мире, измеряя положение и скорость тела в пространстве, мы на него практически не воздействуем. Таким образом, в идеале мы можем одновременно измерить и скорость, и координаты объекта абсолютно точно (иными словами, с нулевой неопределенностью).
В мире квантовых явлений, однако, любое измерение воздействует на систему. Сам факт проведения нами измерения, например, местоположения частицы, приводит к изменению ее скорости, причем непредсказуемому (и наоборот). Вот почему в правой части соотношения Гейзенберга стоит не нулевая, а положительная величина. Чем меньше неопределенность в отношении одной переменной (например, Δx), тем более неопределенной становится другая переменная (Δv), поскольку произведение двух погрешностей в левой части соотношения не может быть меньше константы в правой его части. На самом деле, если нам удастся с нулевой погрешностью (абсолютно точно) определить одну из измеряемых величин, неопределенность другой величины будет равняться бесконечности, и о ней мы не будем знать вообще ничего. Иными словами, если бы нам удалось абсолютно точно установить координаты квантовой частицы, о ее скорости мы не имели бы ни малейшего представления; если бы нам удалось точно зафиксировать скорость частицы, мы бы понятия не имели, где она находится. На практике, конечно, физикам-экспериментаторам всегда приходится искать какой-то компромисс между двумя этими крайностями и подбирать методы измерения, позволяющие с разумной погрешностью судить и о скорости, и о пространственном положении частиц.
На самом деле, принцип неопределенности связывает не только пространственные координаты и скорость — на этом примере он просто проявляется нагляднее всего; в равной мере неопределенность связывает и другие пары взаимно увязанных характеристик микрочастиц. Путем аналогичных рассуждений мы приходим к выводу о невозможности безошибочно измерить энергию квантовой системы и определить момент времени, в который она обладает этой энергией. То есть, если мы проводим измерение состояния квантовой системы на предмет определения ее энергии, это измерение займет некоторый отрезок времени — назовем его Δt. За этот промежуток времени энергия системы случайным образом меняется — происходят ее флуктуация, — и выявить ее мы не можем. Обозначим погрешность измерения энергии Δ Е. Путем рассуждений, аналогичных вышеприведенным, мы придем к аналогичному соотношению для Δ Е и неопределенности времени, которым квантовая частица этой энергией обладала:
Относительно принципа неопределенности нужно сделать еще два важных замечания:
он не подразумевает, что какую-либо одну из двух характеристик частицы — пространственное местоположение или скорость — нельзя измерить сколь угодно точно;
принцип неопределенности действует объективно и не зависит от присутствия разумного субъекта, проводящего измерения.
Иногда вам могут встретиться утверждения, будто принцип неопределенности подразумевает, что у квантовых частиц отсутствуют определенные пространственные координаты и скорости, или что эти величины абсолютно непознаваемы. Не верьте: как мы только что видели, принцип неопределенности не мешает нам с любой желаемой точностью измерить каждую из этих величин. Он утверждает лишь, что мы не в состоянии достоверно узнать и то, и другое одновременно. И, как и во многом другом, мы вынуждены идти на компромисс. Опять же, писатели-антропософы из числа сторонников концепции «Новой эры» иногда утверждают, что, якобы, поскольку измерения подразумевают присутствие разумного наблюдателя, то, значит, на некоем фундаментальном уровне человеческое сознание связано с Вселенским разумом, и именно эта связь обусловливает принцип неопределенности. Повторим по этому поводу еще раз: ключевым в соотношении Гейзенберга является взаимодействие между частицей-объектом измерения и инструментом измерения, влияющим на его результаты. А тот факт, что при этом присутствует разумный наблюдатель в лице ученого, отношения к делу не имеет; инструмент измерения в любом случае влияет на его результаты, присутствует при этом разумное существо или нет.
Что такое принцип неопределенности
Итак, понимание того безумия, которое творится в квантовой физике, было бы очень неполным без одного открытия, который сделал в 1927 молодой немецкий физик Вернер Гейзенберг. Кстати на тот моемент ему было 26 лет, подумайте об этом. Впрочем, его гениальность не помогла отвертеться от участия в немецком ядерном проекте во время второй мировой, и что характерно теория относительности и квантовая физика считались тогда еврейскими лженауками – в общем, бытовые проблемы человечества снова и снова мешали и будут мешать ученым разгадывать тайны мироздания.
Примерно в 20-е и 30-е годы прошлого века в научных кругах шла эпическая битва за правильное понимание законов квантового мира. Проклятых либералов возглавлял Нильс Бор, а консерваторов – лично дедушка Альберт, который, напомню, до конца жизни не верил в квантовую физику. Одним из камней преткновения оказалось вычисление местоположения электрона в атоме и его скорости в определенный момент времени. По странным и непонятным причинам ученые никак не могли вывести формулу для расчета обоих значений одновременно. Эйнштейн говорил, что все эти теоретики неучи и двоечники, потому что чего-то упускают, и бог, знаете ли, не играет со Вселенной в азартные игры. Нильс Бор попивал пивко и утверждал, что классическая физика вообще не применяется для таких случаев как движение электронов. И тут вундеркинд Гейзенберг заявил: все нормально, мужики, так и должно быть.
Давайте вместе ужаснемся открытию на примере. Если пнуть ногой мяч с точно рассчитанной силой, то удивительная и не всем доступная наука физика, в частности классическая механика, легко ответит нам на вопрос, где будет находиться мяч через пять секунд после пинка и какова его скорость. Это же элементарно: расстояние равно время умножить на скорость. Садись, Вовочка, пять по физике!
Теперь мы пнём электроном. По специальным (но все же классическим) формулам считаем его скорость и местоположение на пятой секунде полета и проверяем экспериментом. И получается что-то невероятное. Мы поймали частицу в двух метрах от начала полета, но полученная по результатам эксперимента скорость вообще не такая, да еще и каждый раз разная. И наоборот, чем точнее мы рассчитываем скорость (а вернее импульс, который равен массе, умноженной на скорость), тем хуже себе представляем, где находится частица.
Не в меру умный Гейзенберг объяснил монстрам классической физики, что это не «фигня какая-то», а фундаментальное свойство нашего мира.
И нарисовал им поясняющую формулу: Δx * Δv > h/m, которая означает, что если мы умножим неопределенность положения частицы (длина отрезка координаты, где кажется находится частица) на неопределенность ее скорости (разница между верхней и нижней предполагаемой скоростей этой частицы), то всегда получим число большее нуля, равное массе частицы, поделенной на постоянную Планка (это такая цифра, у которой ноль целых, тридцать три нуля после запятой, а потом уже цифра 6 и другие). Проверьте сами: если мы точно знаем, где находится частица, то есть Δx=0, то тогда ее скорость равна невозможному значению, математической бесконечности, потому что для ее расчета нам придется поделить число из правой части формулы на ноль. А на ноль делить нельзя…
Можете себе представить, как тряхануло весь ученый мир – остальной народ ничего не понял, так как готовился ко Второй Мировой, занимался коллективизацией, пытался вылезти из Великой Депрессии и т.д. и т.п.
Оказалось, что природа защитила свои секреты вот таким вот законом, который никому никогда не обойти. Мы можем узнать вероятные значения параметров частицы с заданной точностью, но никогда не предскажем точно оба параметра. Кроме того принцип Гейзенберга распространяется не только на импульс и местонахождение – он также справедлив для энергии частицы и момента времени, когда частица этой энергией обладает.
Вот формула для самых любознательных читателей: ΔЕ*Δt > h
Цитируя одного замечательного автора: «если бы нам удалось абсолютно точно установить координаты квантовой частицы, о ее скорости мы не имели бы ни малейшего представления; если бы нам удалось точно зафиксировать скорость частицы, мы бы понятия не имели, где она находится. На практике, конечно, физикам-экспериментаторам всегда приходится искать какой-то компромисс между двумя этими крайностями и подбирать методы измерения, позволяющие с разумной погрешностью судить и о скорости, и о пространственном положении частиц«.
Опять же, читатель, лениво прочитавший все вышенаписанное, скажет, мол, товарищи, это все математика и абстракции, мы живем в мире, где поезд выходит из города А в город Б со скоростью, которую нужно рассчитать согласно условиям учебника. Где факты, подтверждающие формулы всех этих немцев и евреев?
Во-первых, мы действительно не можем наблюдать непосредственно этот эффект, потому что различия становятся заметны на очень малых расстояниях (на это нам намекает постоянная Планка в формуле с ее тридцатью тремя нулями после запятой). А во-вторых, принцип неопределенности не так и чужд нашей Вселенной, а очень многое объясняет, почему вещи устроены так как сейчас, а не иначе.
Например, становится ясно, почему существует твердая материя.
Не могу не процитировать еще одного хорошего автора: «что случится с электроном, если его начнут слишком сильно прижимать к ядру. Это будет означать, что его местоположение станет известным с большой степенью точности. Но, согласно принципу неопределенности Гейзенберга, чем больше мы уверены в местоположении частицы, тем меньше мы уверены в ее импульсе. Это очень похоже на то, как если бы мы засунули пчелу в спичечный коробок. Встряхните коробок — пчела разозлится и будет с остервенением колотиться о стены своей тюрьмы. Вот электроны в атомах и есть те самые пчелы в коробках. Когда мы ступаем по земле, наш вес сжимает атомы, из которых она состоит. Это сжатие заставляет электроны хоть чуть-чуть, но приблизиться к ядрам. А принцип неопределенности Гейзенберга понуждает их воспротивиться и оттолкнуться от ядер«.
Еще один пример действия квантовой неопределенности мы уже встречали в нашей статье про вакуум. Теперь стало немного понятнее, почему вакуум не может существовать с точки зрения квантовой физики: вакуум это поле с нулевой энергией и нулевым количеством частиц. А этого одновременно быть не может, поэтому природе приходится создавать квантовую пену, лишь бы обойти дурацкий запрет на точное знание всех параметров частиц.
Тем не менее, многие люди, включая даже настоящих ученых, полагают, что неопределенность измерения можно объяснить классическими средствами. Ведь что получается, говорят эти люди, если мы пытаемся измерить местоположение частицы, то для этого мы должны как-то обнаружить ее в пространстве и для этого мы ставим для нее преграду или ловим потоком других частиц (фотонами, например). Если в макромире освещение фонариком предмета не приведет к изменению параметров предмета, то в микромире ситуация другая. Длина волны фотона сопоставима с длиной волны разыскиваемой частицы и их «столкновение» фатально для системы.
Если фотон имеет очень большую длину волны, мы не можем точно определить положение частицы. Фотоны с большой длиной волны ударяют слабо, поэтому измерение не слишком влияет на электрон, а значит, мы можем определить его скорость достаточно точно. С другой стороны, чтобы как следует понять, где находится частица, нужно ударить ее фотоном с маленькой длиной волны. Фотон с маленькой длиной волны очень энергичный, а значит, сильно ударяет частицу. В результате мы не можем определить ее скорость достаточно точно. (тоже цитата)
Интереснейшим практическим следствием неопределенности является туннельный эффект.
Если по каким-то причинам местонахождение частицы становится все более и более определенным, то скорость частицы становится, как мы знаем, непредсказуемой. Строго говоря, непредсказуемым становится импульс частицы. Вследствие этого обычного квантового явления неопределенность импульса может дать частице дополнительную энергию и такая частица иногда может сделать очень странную вещь: пройти сквозь непреодолимый барьер. В макромире это выглядело бы как прохождение сквозь стену или выпрыгивание из ямы без видимых причин.
Но туннелирование в самом деле существует. И мы им пользуемся в таких достижениях прогресса как туннельный диод или сверхпроводники. Тот же радиоактивный распад существует благодаря эффекту туннелирования: альфа-частицы отрываются от тяжелого ядра не за счет собственных сил – ядро их на самом деле очень крепко держит (мы как-то уже рассказывали про сильное взаимодействие) – а как раз из-за существования ненулевой вероятности прорваться через энергетический барьер. И существование термоядерного синтеза внутри звезд (из-за которого наше солнце светит) также обусловлено туннелированием. Вот ведь как все на самом деле-то, котаны.
Как мы уже говорили, Эйнштейну очень не нравились всякие неопределенности в физике. И в то время, когда Нильс Бор пытался создать хоть какое-то подобие квантовой теории, Эйнштейн всячески изводил его провокационными вопросами. Так в 30-е годы Эйнштейн и два его единомышленника – Подольский и Розен – предложили так называемый ЭПР-парадокс (по первым буквам фамилий хитрых физиков), гипотетический эксперимент, который доказывал, что неопределенность Гейзенберга можно обойти. Те, кто немного разбирались в том, что происходит, запасались попкорном и издалека наблюдали как физики троллят друг друга. Заголовок газеты тех времен гласил: «Эйнштейн атакует квантовую теорию: Учёный и двое его коллег находят её „неполной“, хотя и „корректной“
Попробуем упрощенно разобрать суть парадокса. Допустим Гейзенберг немного прав, и мы почему-то не можем измерить импульс и координаты частицы одновременно. Но попробуем пойти в обход. Давайте столкнем две частицы, и после удара они разлетятся, получив некоторые общие характеристики. Такие частицы физики называют «запутанными«. Отбросив сложную матчасть, вспомним закон сохранения импульса из классической механики – суммарный импульс тел до соударения равен суммарному импульсу после соударения. Итак, частицы сталкиваются, и они разлетаются, поделив импульс, как биллиардные шары после столкновения. Затем мы измеряем координату у первой частицы и импульс у второй. Таким образом узнаем и координату первой частицы (которую измерили непосредственно), и ее импульс (который просто вычислили, измерив импульс у второй частицы и отняв ее от первоначального импульса до соударения).
И только спустя 30 лет, один физик по имени Белл придумал специальную формулу, с помощью которой можно было бы проверить, кто прав Эйнштейн или Бор. А еще 22 года спустя (в 1982 году) французские ученые сумели поставить эксперимент и проверили результаты по формулам Белла. Оказалось, что прав был Нильс Бор: Никакой «объективной физической реальности», о которой грезил Эйнштейн, в микромире не существует.
На картинке еще одно более сложное, но все-таки популярное объяснение ЭПР-парадокса (разбирайтесь сами).
Квантовая запутанность крайне сложная вещь – о ней и прочих страшных вещах (квантовая нелокальность, квантовые компьютеры, все эти необъяснимые спины, запрет Паули, неравества Белла и т.д.) мы как-нибудь попробуем рассказать в следующих ликбезах от дружного коллектива Quantuz, если, конечно, рейтинги статей дадут нам понять, что народу эта тема все еще интересна. Искренне просим прощения за возможные неточности в изложении. Напоминаем, что наша цель как можно более популярно объяснить людям, почему физика интереснее «битвы экстрасенсов».
Помните, что если вы что-то не поняли, то это нормально. Квантовую физику мало кто понимает целиком. Не унывайте.