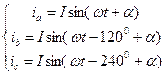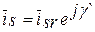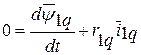что такое преобразование парка горева

Уравнения Парка – Горева для синхронной машины.

Уравнения Парка — Горева связывают между собой мгновенные значения токов, магнитных пото­ков, напряжений в осях координат (d, q), связанных с ротором.

Мгновенные значения параметров режима опре­деляют как проекции на оси времени фаз а, b, с вектора тока (напряжения, ЭДС, потокосцепления), вращающегося с угловой ско­ростью . Этот вектор тока называют обобщенным.

Оси времени t_a, t_b, t_c фаз a, b, с неподвижны и совпадают с осями обмоток статора (рис. 2.1). Мгновенные значения фазных токов равны:

где — произвольный угол.

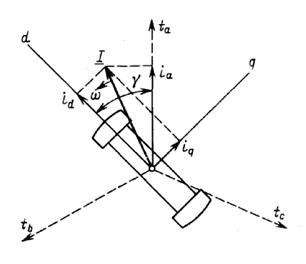
Рис.2.1 Обобщенный вектор тока 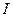и его проекции на временные оси.

Проекции обобщенного вектора тока на оси d, q, связанные с ротором, дают значения продольного и поперечного токов (рис. 2.2):

При наличии токов нулевой последовательности

Соотношения, аналогичные приведенным выше, справедливы для напряжений, ЭДС и потокосцеплений.

Рис. 2.2. Обобщенный вектор тока I и проекции его

на продольную и поперечную оси ротора

Связь между мгновенными значениями фазных величин и величин в продольной и поперечной осях устанавливается на основе уравнений:

Угол меняется во времени:

где — полное потокосцепление статора в продольной и поперечной осях.

В случаях симметричного режима энергосистемы токи нулевой последовательности отсутствуют ( = 0).

Значения потокосцепления статора в поперечной и продольных осях определяются из вы­ражений:

= G (р) U_f + X_d (р) i_d

= X_q (p) ,

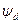
где G(p)—операторная проводимость маши­ны;

X_d(p), X_q(p) — операторные сопротивления машины в продольной и поперечной осях;

U_f — напряжение возбуждения машины.

Для машины без демпферных обмоток и эквивалентных им контуров:

;

;

.

Если известна ЭДС 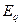, то

,

где — постоянная времени обмотки возбуждения машины при разомкнутой обмотке статора;

— активное сопротивление обмотки статора по продольной оси;

— реактивное сопротивление взаимной индукции обмотки возбуждения со статором в продольной оси;

— реактивное сопротивление индуктивности ротора в продольной оси.

Для машины с демпферными обмотками значения потокосцепления статора в поперечной и продольных осях 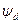и определяются теми же уравнениями.

Рис.2.3 Основные параметры синхронной машины для принятых направлений осей.

Уравнения Парка – Горева для принятых на рис.2.3. направлениях осей примут вид:

;

;

;

где 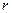— активное сопротивление статора;

— активное сопротивление статора нулевой последовательности;

; ;

.

В системе относительных единиц , поэтому .

Третье уравнение системы относится к слу­чаю несимметричного режима или несиммет­ричной схемы.

Уравнения, приведенные выше, полностью описывают переходный процесс машины, ра­ботающей на шины неизменного напряжения. Для анализа переходного процесса в сложной энергосистеме уравнения составляются для каждого эле­мента (генераторов, нагрузок, участков сети) и решаются совместно.

Решение системы урав­нений Парка – Горева относительно токов или других величин, рассматриваемых как неизвестные, проводится в операторной форме (для изобра­жений), например находятся значения токов

; ;

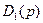
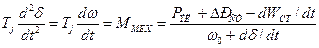
где , D₂ (p) — миноры определителя систе­мы; D (р) — главный определитель системы.

,

где — постоянная инерции машины.

Для определения параметров при переходных процессах можно использовать упрощенные уравнения Парка – Горева. Для получения этих уравнений отказы­ваются от учета влияния:

1) апериодической составляющей тока ста­тора (трансформаторной ЭДС);

2) периодических токов ротора, связанных с апериодическими составляющими тока ста­тора;

3) активного сопротивления в цепи ста­тора.

; .

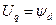
Данные уравнения положены в основу рас­четов периодической составляющей токов короткого замыкания при обычно принимаемых допущениях.

При принятых предпосылках отдаваемая мощность численно равна вращающемуся моменту; поэтому для симметричного режима или режима, условно приведённого к симметричному,

.

Уравнение относительного движения ротора

.

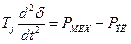
На основе этих расчетных уравнений (их иногда называют уравнениями Лонглея или уравнениями Лебедева — Жданова) обычно ведутся проектные и эксплуатацион­ные расчеты устойчивости. Они позволяют для расчетов переходных процессов пользоваться соотношениями, вытекающими из векторной диаграммы установившегося режима [рис.2.1].

Источник

Уравнения Парка-Горева синхронной машины

Уравнение электрического равновесия цепи статора, записанное через изображающие векторы напряжений, токов и потокосцеплений в неподвижной системе координат, имеет вид

где ;

w_с – угловая частота напряжения, которая при работе синхронного генератора параллельно с системой неограниченной мощности равна синхронной.

Это же уравнение в системе координат, вращающейся со скоростью ротора w_r, получим, используя выражение для перехода изображающего вектора во вращающейся системы координат к неподвижной, которое, например, для тока имеет вид

где — изображающий вектор тока статора в неподвижной системе координат;

— изображающий вектор тока статора во вращающейся системе координат;

— угол между магнитной осью фазы А и осью d ротора.

,

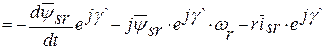
т.к. .

В результате, в системе d, q, 0, вращающейся со скоростью ротора w_r, уравнение равновесия цепи статора, записанное через изображающие векторы, имеет вид

.

Уравнения равновесия напряжений ротора

,

,

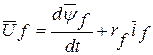
при этом остаются неизменными, так как входящие в него величины с самого начала определялись именно в системе координат ротора.

Выразим изображающие векторы через их составляющие по осям вращающейся комплексной плоскости, помня, что действительная ось комплексной плоскости направлена вдоль оси d, а мнимая ― вдоль отрицательного направления оси q. В результате получаем :

,

,

,

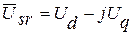
Подставив эти выражения в выражение для , получим:

.

Приравнивая отдельно действительные и мнимые части, получим

,

,

,

, (4.1)

,

.

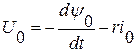
Эта система уравнений должна быть дополнена ещё уравнением движения или механического равновесия моментов на валу

,

.

Здесь М_внешн. – вращающийся момент турбины для генератора М_т или момент механизма М_мех для двигателя;

w_r – угловая скорость ротора;

— электромагнитный момент;

J – момент инерции вращающихся масс ротора, выраженный в кг×м 2

Преобразование переменных статора в системе координат А, В, С в новые переменные, связанные с системой координат d, q, 0 являясь формально математическим приёмом, имеет простое физическое объяснение.

При преобразовании переменных трёхфазная обмотка статора заменяется эквивалентной двухфазной, жёстко связанной с осями d и q ротора (вращается с той же скоростью, что и ротор со скоростью w_r ротора).

Дифференциальные уравнения равновесия дополним алгебраическими, связывающими потокосцепления и токи соответствующих контуров.

1) в продольной и поперечной осях машины, кроме потоков рассеяния существуют потоки в воздушном зазоре, пронизывающие все контуры, расположенные по соответствующим осям машины;

2) все параметры роторных контуров приведены к статору ( как – уточним позднее)

Тогда выражения для потокосцеплений статорных и роторных контуров, входящих в систему (2), имеют вид

,

,

, (4.2)

,

,

.

Так как преобразованные обмотки статора d и q неподвижны относительно ротора, то индуктивности и взаимные индуктивности этих обмоток, входящие в выражения (2), постоянны, если не учитывать изменения насыщения магнитной цепи. Таким образом, преобразование переменных (переход от системы координат А, В, С к осям d и q) позволяет избавиться от периодических коэффициентов в дифференциальных уравнениях (1) синхронной машины.

Уравнения (1) и (2) выражают основу теории обобщённой электрической машины.

При постоянной частоте вращения ротора (w_r = const) с учётом принятых допущений система уравнений (1) и (2) становится системой линейных дифференциальных уравнений, допускающей аналитическое решение, то есть можно получить аналитическое выражение для изменения тока статора во времени при коротком замыкании.

В системе (1) первые слагаемые первых двух уравнений для обмоток d и q статора представляют ЭДС трансформации, поскольку они вызываются изменением величин соответствующих потокосцеплений, а вторые слагаемые – ЭДС вращения. В установившемся режиме ЭДС трансформации отсутствуют.

В рассмотренной выше модели синхронной машины, соответствующей уравнениям Парка-Горева, ЭДС вращения представлены лишь частично, так как при синхронном вращении обмоток и магнитных потоков никаких ЭДС вращения в этих обмотках нет. Только при перемещении обмоток относительно вращающихся магнитных потоков, что в общем случае также имеет место при переходном процессе, в обмотках наводятся дополнительные ЭДС вращения (точнее ЭДС скольжения ― в обмотке d и в обмотке q, где w_r ¹ w_с), поток при работе СМ параллельно с системой неограниченной мощности всегда вращается с синхронной скоростью.

Источник

Что такое преобразование парка горева

УНИВЕРСАЛЬНЫЙ ПОДХОД К МОДЕЛИРОВАНИЮ ПЕРЕХОДНЫХ ПРОЦЕССОВ В СИНХРОННВХ МАШИНАХ НА ОСНОВЕ СЛОЖНЫХ СХЕМ ЗАМЕЩЕНИЯ РАЗЛИЧНЫХ СТРУКТУР

А.М. ЛАРИН, И.И. ЛАРИНА

ГВУЗ «Донецкий национальный технический университет»

Источник: Наукові праці Донецького національного технічного університету серія «Електротехніка і енергетика», випуск 11(186), стор. 230 – 234.

Предложен единый подход к математическому моделированию переходных процессов в синхронных машинах на основе сложных детализированных эквивалентных схем замещения путем предварительного их преобразования к одному виду, удобному для аналитического описания с помощью дифференциальных уравнений Парка-Горева.

Введение. Одна из областей теории синхронных машин (СМ) – исследование процессов в различных режимах работы – основывается на том, что предполагается известной определенная совокупность активных и индуктивных сопротивлений, отражающих связь между токами и потокосцеплениями в магнитносвязанных контурах машины. Такая исходная информация представляется в форме схем замещения физически обоснованных структур, имеющих различную степень детализации. Известно большое число точных детализированных сложных схем замещения СМ с различными структурами, отражающими взаимные связи отдельных конструктивных элементов машины 6. Каждый тип синхронного генератора с учетом особенностей конструкции ротора, представляется отдельной схемой замещения. Такие схемы используют в проектных организациях и в заводской практике для уточненного исследования распределения токов в демпфирующих контурах, влияния параметров различных участков конструкции на результирующие параметры машины и влияния насыщения этих участков на параметры и распределение токов. Их применяют также к расчету установившихся анормальных режимов, связанных с большими скольжениями (несимметричная нагрузка, несимметричные короткие замыкания, неполнофазные режимы). Анализ электромеханических переходных процессов для мгновенных значений параметров режима с помощью таких сложных эквивалентных схем высокого порядка вызывает принципиальные сложности. При расчете переходных процессов, например в операторной форме, это приводит к сложным операторным выкладкам, не всегда дающим возможность при практических расчетах выполнить переход во временную область. При этом для глубокого исследования различных режимов необходимо разрабатывать индивидуальное программное обеспечение для ПЭВМ, реализующее соответствующие математические модели. Одна из таких программ «ARTS» разработана в ИЭД НАН Украины для расчетов установившихся асинхронных режимов турбогенераторов при их представлении многозвенными электрическими схемами [6]. Поэтому использование сложных детализированных схем к моделированию промышленных машин в условиях эксплуатации, особенно когда имеет место влияние элементов питающей сети, неэффективно.

Вместе с тем имеется широкий круг задач, когда достаточно только точно определить распределение токов в контуре обмотки возбуждения (ОВГ) и эквивалентно в массивных конструктивных элементах ротора (ДС).

В общем комплексе проблем исследования переходных процессов и устойчивости энергосистем актуальной является задача рационального математического моделирования электрических машин переменного тока.

В этой связи целесообразна постановка задачи, направленная на разработку методов преобразования сложных детализированных схем замещения к виду, удобному для моделирования переходных процессов по дифференциальным уравнениям типа уравнений Парка-Горева. При этом необходимо, чтобы в упрощенных схемах достоверно определялись параметры переходных режимов как в обмотке статора, так и в обмотке возбуждения. Это позволит составить универсальную программу расчета на ПЭВМ для исследования различных видов переходных процессов.

Целью настоящей работы является разработка обобщенного подхода к преобразованию сложных эквивалентных схем замещения различных структур к одному виду, наиболее удобному для моделирования переходных процессов по дифференциальным уравнениям Парка-Горева на основе единой универсальной программы для ПЭВМ.

Материалы и результаты исследований. Для анализа протекания электромеханических переходных процессов во времени, как правило, используются упрощенные схемы замещения, на основании которых составляются дифференциальные уравнения типа уравнений Парка-Горева. Расчеты электромагнитных и электромеханических переходных процессов в синхронных машинах без учета влияния насыщения по полным уравнениям Парка-Горева позволяют учитывать влияние неограниченного числа контуров на роторе. ОВГ в этом случае представляется в эквивалентной схеме одним контуром с независящими от частоты параметрами (рис.1).

Обычно используют уравнения, записанные в следующем виде:

(1)

Потокосцепления любой обмотки в (1) могут быть выражены на основе собственных и взаимных индуктивных сопротивлений следующим образом:

, (2)

где — взаимная индуктивность между i и j обмотками. Если i=j, то индуктивное сопротивления является собственным.

Очевидно, что для сложных схем замещения определение собственных и взаимных индуктивных сопротивлений, связывающих токи и потокосцепления, представляет достаточно сложную задачу. При этом на каждом шаге интегрирования уравнений (1) необходимо несколько раз решать систему линейных алгебраических уравнений (2) относительно токов. Поэтому непосредственное использование для математического моделирования по дифференциальным уравнениям Парка-Горева схем замещения сложных структур неэффективно. Для схемы замещения общепринятого типа (рис.1), в которой обмотка возбуждения представлена одним контуром, в [7] предложен способ интегрирования уравнений вида (1), не требующий решения системы алгебраических уравнений. Используемые для определения токов проводимости при этом рассчитываются до начала процедуры интегрирования уравнений.

Метод упрощения сложных схем замещения путем их преобразования к виду, удобному для моделирования по уравнениям (1) изложен в [8]. Способ основан на том, что кроме соблюдения адекватности частотных характеристик исходной и преобразованной схем замещения синтез последней необходимо осуществлять при равенстве комплексного коэффициента распределения тока статора в ветви ОВГ (). В этом случае ветвь ОВГ будет уже представляться самостоятельной многоконтурной цепью (рис.2).

Схемы замещения вида, представленного на рис.2, могут быть также определены экспериментально, по данным опытов внезапного трехфазного короткого замыкания [9]. Получаемые в этом случае параметры эквивалентных схем замещения, которые рассчитываются непосредственно по данным обработки переходных функций токов в обмотках статора и возбуждения в опыте внезапного трехфазного короткого замыкания соответствуют короткозамкнутому состоянию обмотки возбуждения. Такие схемы замещения непосредственно можно использовать только для исследования переходных процессов, имеющих место при короткозамкнутом состоянии ОВГ. При анализе динамических режимов, имеющих место при включении в цепь обмотки возбуждения дополнительного (чаще всего активного) сопротивления необходимо предварительно выполнить ряд расчетных процедур.

Рассчитать частотную характеристику результирующей проводимости ветви ОВГ после включения дополнительного активного сопротивления :

. (3)

По найденной частотной характеристике выполнить синтез параметров многоконтурной обмотки возбуждения новой схемы замещения. Параметры, отражающие влияние демпферной системы остаются прежними.

Очевидно, что такой подход является неэффективным. Поэтому целесообразно синтезировать схемы замещения различных структур, в которых в последовательной цепи было бы выделено известное активное сопротивление обмотки возбуждения (рис.3).

Синтез параллельных индуктивно-активных цепочек, отражающих влияние обмотки возбуждения генератора (,,…;,,…) при этом во всех случаях должен осуществляться на основе частотных характеристик проводимости ОВГ без учета ее активного сопротивления :

. (4)

Для математического моделирования переходных процессов на основе схемы замещения, в которой ОВГ учитывается многоконтурностью (рис.3) с выделенным активным сопротивлением, была уточнена приведенная система дифференциальных уравнения Парка-Горева (1). Дополнения состоят в том, что число уравнений, отражающих влияние обмотки возбуждения, должно соответствовать числу контуров, характеризующих ее в схеме замещения. Кроме того, учитывается активное сопротивление ОВГ, вынесенное в последовательную цепь. Моделирование с дополнительным активным сопротивлением в ОВГ осуществляется, в этом случае, путем соответствующего увеличения значения активного сопротивления ОВГ.

Тогда в уточненной системе дифференциальных уравнений, описывающих электромагнитные и электромеханические переходные процессы, применительно к схеме замещения вида, показанного на рис.3, должно быть изменено уравнение, описывающее процессы в ОВГ. Последнее будет иметь следующий вид:

(5)

Значения токов в (1) с учетом (5) определяются в соответствии с [7].

Уточненная система уравнений была реализована в виде программы расчета электромеханических переходных процессов для ПЭВМ в среде прикладного пакета MathCAD. Эффективность предложенного подхода оценивалась путем математического моделирования переходных режимов в турбогенераторе типа ТГВ-200М. На основе его исходной детализированной схемы замещения, показанной на рис.4, в соответствии с [8] была синтезирована схема замещения вида, представленного на рис.3. Значения параметров последней приведены в табл.1.

Тип схемы замещения

Значения параметра, о.е.

1,916

Источник