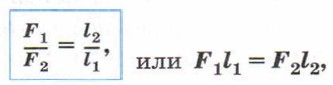что такое правило равновесия рычага

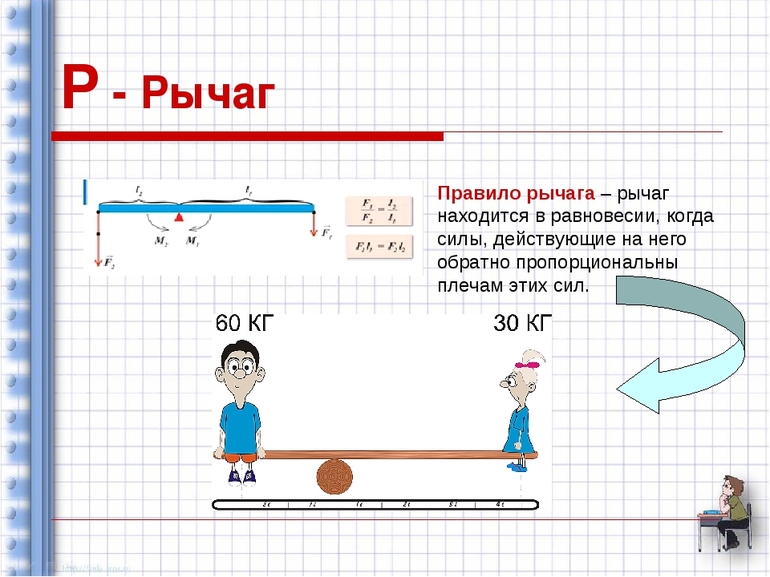
Правило равновесия рычага

4. На основании подобных опытов более двух тысяч лет назад древнегреческим учёным Архимедом было установлено правило:

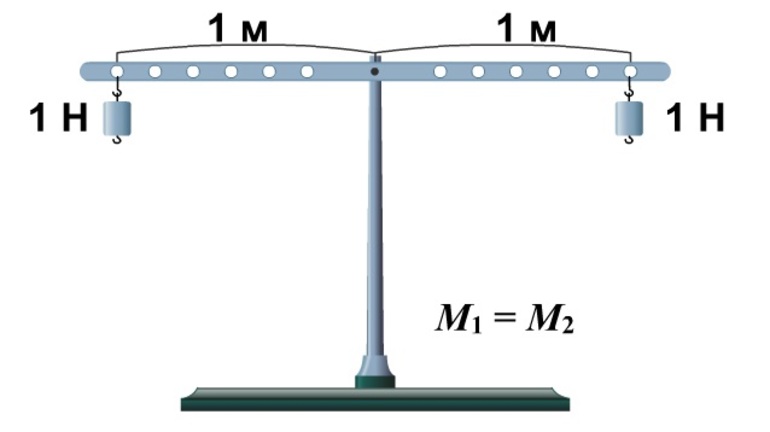
рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны плечам этих сил.

Это правило (условие) равновесия рычага записывают в виде формулы:

где F₁ и F₂ — силы, действующие на рычаг, l₁ и l₂ — плечи этих сил.

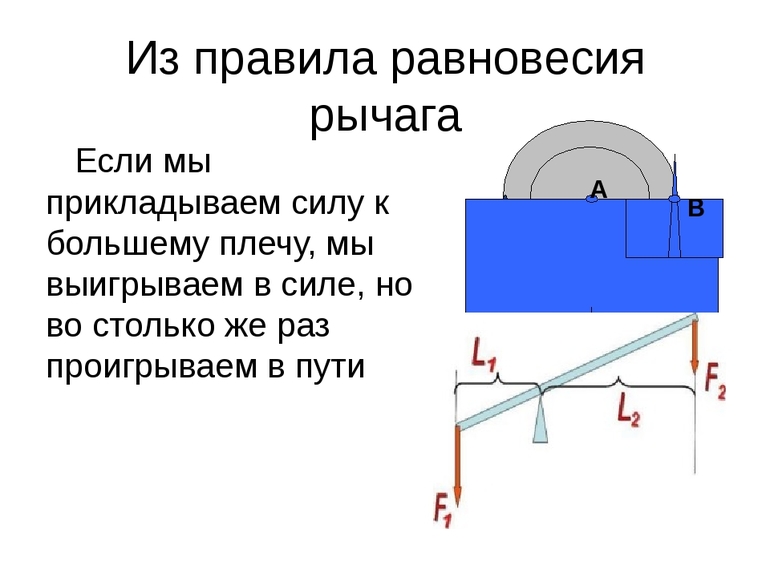
Зная правило равновесия рычага, можно объяснить, как с помощью простого механизма получить выигрыш в силе. Если к длинному концу рычага приложить небольшую силу, то можно уравновесить гораздо большую силу, приложенную к короткому концу рычага.

5. Как можно объяснить выигрыш в силе в примере с тачкой (см. рис. 93), используя правило равновесия рычага?

Силы ₁ и ₂, действующие на тачку, параллельны друг другу и направлены в противоположные стороны. Сила ₂ стремится вращать рычаг по ходу часовой стрелки, а сила ₁ — против её хода.

Плечи сил ₁ и ₂ соответственно равны l₁ и l₂. По правилу равновесия рычага плечо l₂ много меньше плеча l₁, следовательно, чтобы уравновесить рычаг, сила ₁ может быть меньше ₂. Выигрыш в силе очевиден.

6. В основе действия многих машин и механизмов, используемых в быту и технике, лежит правило равновесия рычага. Вы уже знакомы с устройством и принципом действия рычажных весов. Они именно так и называются — «рычажные весы», потому что их основной элемент — рычаг.

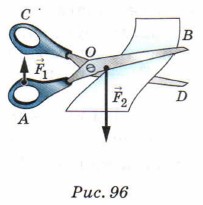
Рассмотрите внимательно обычные ножницы (рис. 96). Они представляют собой пару рычагов, скреплённых в точке О, относительно которой они могут вращаться. Будем считать, что рычаг CD остаётся в покое, а к концу рычага АВ в точке А прикладывается сила ₁ — сила пальцев человека, работающего ножницами. Сила ₂, действующая со стороны рычага на листок бумаги, окажется много больше приложенной силы ₁. На том же принципе основана работа и многих других инструментов: клещей, плоскогубцев, садового секатора и пр.

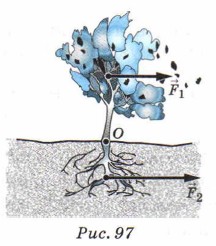
Рычаг встречается повсеместно в живой и неживой природе. Объясняя, например, причину падения деревьев во время урагана, придётся вспомнить о правиле равновесия рычага. Сила сопротивления земли (₂), действующая на корни дерева (рис. 97), может в какой-то момент оказаться недостаточной, чтобы удержать дерево в равновесии, и дерево упадёт под напором порыва ветра (сила ₁).

В организме человека и животного, в теле птиц и насекомых очень много различных рычагов. Только в вашем теле более 200 различных костных рычагов. Очень интересный вывод можно сделать, рассмотрев действие рычага в локтевом суставе человека (рис. 98). В этом рычаге точка опоры (точка О) находится в суставе. Вес груза ₂ приложен к концу рычага, а сила ₁, необходимая для удержания груза, приложена вблизи от точки О. Сила ₁ возникает благодаря сокращению мышц руки человека. В соответствии с правилам равновесия рычага сила ₁ должна быть много больше силы ₂, так как плечо l₁ намного меньше плеча l₂. В данном случае рычаг даёт проигрыш в силе, но выигрыш в расстоянии. Оказывается, сила мышц руки человека гораздо больше веса груза, который он поднимает рукой.

Источник

Что такое правило рычага: применение в прошлом и нынешнем времени

Для обеспечения максимально продуктивного труда с давних времен человечество использует правило рычага, это один из самых простых и действенных механизмов. Подробное рассмотрение техники исполнения процесса и формул поможет разобраться в вопросе тщательнее. Не менее важно знать, где можно применить это правило, и какие виды использования были освоены в различных сферах деятельности.

Понятие в физике

Довольно простой механизм состоит из основных частей, первая – это доска, она нужна для надавливания на одну из сторон с помощью противоположных сил. Второй составляющей процесса является опора, она служит осью вращения, именно вокруг этой основы крутится балка. В зависимости от расстановки всех элемента существует понятие о 3 типах использования правила рычага. «Плечо» – это зачастую доска, которая расположена непосредственно на основании, при этом важно наличие воздействующей силы с обеих сторон. Рычаг нужен для преобразования силы, направленной на перемещение или поднятие, это необходимо чтобы облегчить рабочий процесс.

Факты из прошлого

Ответить точно на вопрос, когда стали использовать правило рычага не представляется возможным, известно лишь то, что еще в Египте и Месопотамии этот прием был распространен. Они применяли конструкции такого плана для подъема сосудов с жидкостью из реки или колодцев. Письменным доказательством был труд Плутарха «Параллельные жизни», в котором, по словам очевидцев, Архимед с помощью правила рычага смог подвесить в воздух корабль с находящимися на борту людьми. Теоретически человечество с самого начала существования пользовалось этим приемом сами того не подозревая, ведь строение тела человека предполагает проявление подобной функции, а именно в предплечьях и плечах.

Момент силы и основное правило

Чтобы подробнее рассмотреть применение рычага, нужно разобраться в деталях, математически формула выглядит так: M = d*F. Здесь F выступает в роли воздействующей силы, а d будет плечом, которое равно длине от первой точки до основы. Чтобы определить момент М, нужно знать расположение оси, иначе делать выводы о правильной нагрузке нельзя. Рычаг классического образца с двумя плечами подвергается воздействию 2 сил:

В первом варианте это манипуляция, которая представляет усилие людей, а во втором значение относящееся к нагрузке на некий элемент. Правило равновесия рассчитается по формуле: R*dR – F*dF = 0, а перевод в правую часть вычисляется так: R*dR = F*dF.

Важные моменты процесса

Нужно точно понимать что, используя, правило рычага на практике, сохранится энергия системы, без определенной работы груз доставить на высоту не получится. Для совершения манипуляций могут потребоваться большие или малые усилия, все будет зависеть от длины конца балки, начинающейся от оси. Для максимальной продуктивности нужно перетащить плечо в вертикальном положении и выставить соответствующую величину. Эту разницу называют выигрышем и проигрышем рычага.

Общепринятые виды

Существует 3 типа манипуляций, которые классифицируются по соотношению сил и оси, выглядит все так:

Прежде чем взяться за исполнение определенной работы, стоит продумать, какой вариант будет выгоднее всего, в противном случае все усилия, потраченные на применение правила рычага будут напрасными.

Решение задачи

Ручная тачка, оборудованная одним колесом, также относится к ряду изделий, где используется рассматриваемый прием. Нужно правильно рассчитать груз, который можно положить на нее. Поскольку центр массы расположен на 1/3 длины, а вертикальные усилия человека 200 Н, вычисление происходит так: F*l = R*1/3*l, F = m*g/3, m = 3*F/g = 3*200/9,81 ≈ 61 кг. Получается, что можно выиграть в силе 3 раза, ведь показатель 200 Н равняется телу с массой 20,4 кг.

Источник

Рычаг. Равновесие сил на рычаге

Содержание

С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.

Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.

Рисунок 1. Строительство пирамид по Геродоту (гравюра XVIII века).

В данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.

Устройство рычага

Рычаг – это любое твердое тело, которое может вращаться вокруг неподвижной опоры.

Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.

В обоих случаях у этого рычага есть неподвижная точка опоры – точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.

Сила, с которой Образавр действует на палку (рычаг) меньше веса камня, но, тем не менее, у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.

Таким образом, рычаги бывают двух видов (рисунок 3):

Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.

Условие равновесия рычага

Рисунок 4. Рычаг.

Рисунок 5. Схематическое изображение рычага.

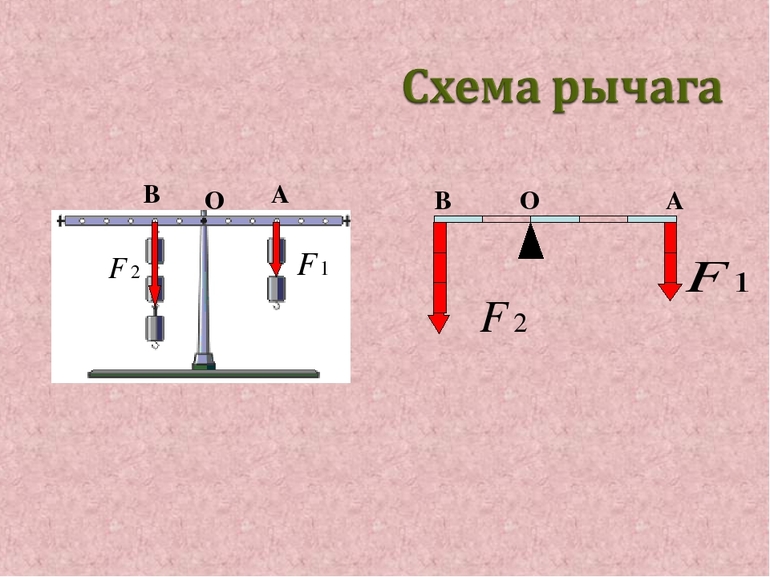
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.

Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.

С помощью таких опытов было установлено правило равновесия рычага:

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил

Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют – правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: “Дайте мне точку опору, и я переверну Землю!”.

Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.

Примеры задач

Показать решение и ответ

Решение:

Запишем правило равновесия рычага:

$F_1 = F_2 \cdot \frac = gm \cdot \frac = 9.8 \frac<Н> <кг>\cdot 300 \space кг \cdot \frac<0.6 \space м> <3 \space м>= 2940 \space Н \cdot 0.2 = 588 \space Н$.

СИ:
$0.1 \space кг$
$0.2 \space кг$
$0.5 \space м$
$0.2 \space м$

Показать решение и ответ

$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 \frac<Н> <кг>\cdot (0.1 \space кг + 0.2 \space кг) = 9.8 \frac<Н> <кг>\cdot 0.3 \space кг \approx 3 \space Н$.

Запишем правило равновесия рычага:

Найдем массу груза:

$m_3 = \frac = \frac<1.2 \space Н><9.8 \frac<Н><кг>> \approx 0.1 \space г = 100 \space г$.

Источник

Рычаг: условие равновесия. Условие равновесия рычага: формула

Мир, который нас окружает, находится в постоянном движении. Тем не менее существуют системы, которые могут находиться в относительном состоянии покоя и равновесия. Одной из них является рычаг. В данной статье рассмотрим, что он собой представляет с точки зрения физики, а также решим пару задач на условие равновесия рычага.

Что такое рычаг?

В физике рычагом называется простой механизм, состоящий из невесомой балки (доски) и одной опоры. Расположение опоры не является фиксированным, поэтому она может находиться ближе к одному из концов балки.

Вам будет интересно: Что такое фурор? Желание выделиться или следствие страха?

Действующие на рычаг силы

Данная статья посвящена условиям равновесия рычага. Любое равновесие в статике (раздел физики, изучающий тела в покое) предполагает наличие или отсутствие сил. Если рассматривать рычаг в свободном виде (невесомая балка и опора), то на него не действуют никакие силы, и он будет находиться в равновесии.

Когда с помощью рычага любого типа выполняют работу, то на него всегда действуют три силы. Перечислим их:

Условие равновесия рычага предполагает рассмотрение не столько отмеченных действующих сил, сколько моментов сил, создаваемых ими.

Что такое момент силы

В физике моментом силы, или вращающим моментом, называют величину, равную произведению внешней силы на плечо. Плечом силы называют расстояние от точки приложения силы до оси вращения. Наличие последней является важным при расчете момента силы. Без наличия оси вращения нет никакого смысла говорить о моменте силы. Учитывая приведенное определение, можно записать следующее выражение для вращающего момента M:

Помимо формулы выше, следует запомнить, что если сила F стремится повернуть систему так, что та начинает движение против часовой стрелки, то создаваемый момент считается положительным. Наоборот, стремление повернуть систему по ходу стрелки часов свидетельствует об отрицательном вращающем моменте.

Формула условия равновесия рычага

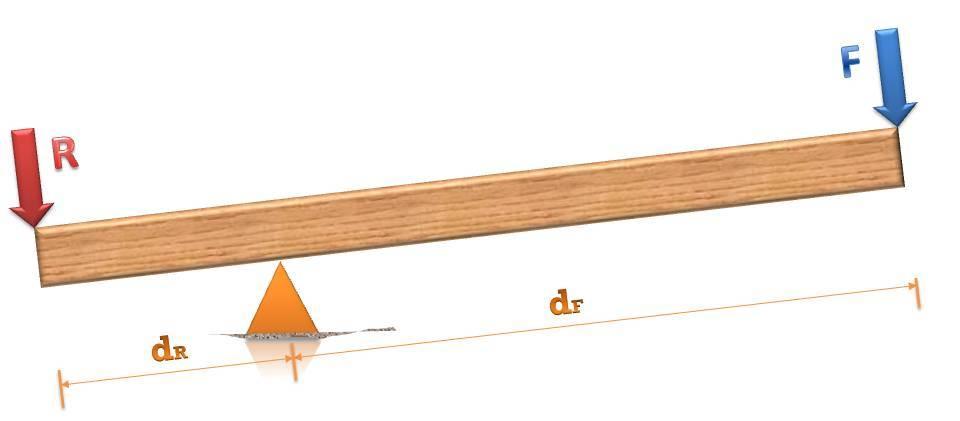
На рисунке ниже показан типичный рычаг, а также отмечены значения его правого и левого плеч. Внешняя сила обозначена буквой F, а вес груза, который следует поднять, обозначен буквой R.

В статике для того, чтобы система покоилась, необходимо выполнение двух условий:

Первое из названных условий означает отсутствие поступательного перемещения системы. Оно очевидно для рычага, поскольку его опора прочно стоит на полу или земле. Поэтому проверка условия равновесия рычага предполагает только проверку справедливости следующего выражения:

Поскольку в нашем случае действуют только три силы, перепишем эту формулу следующим образом:

Сила реакции опоры момента не создает. Последнее выражение перепишем в виде:

Это и есть условие равновесия рычага (в 7 классе общеобразовательных школ в курсе физики оно изучается). Формула показывает: если значение силы F будет больше веса груза R, то плечо dF должно быть меньше плеча dR. Последнее означает, что, прилагая большую силу в течение небольшого пути, мы можем переместить груз на большое расстояние. Справедлива и обратная ситуация, когда F dR. В этом случае выигрыш наблюдается в силе.

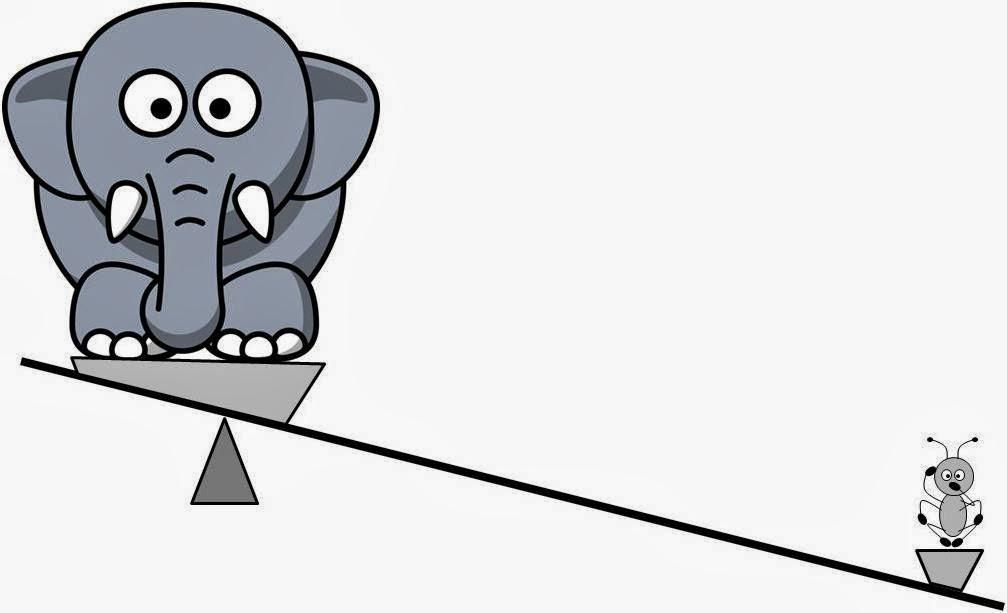
Задача со слоном и муравьем

Многим известно знаменитое высказывание Архимеда о возможности с помощью рычага сдвинуть целый земной шар. Это смелое заявление имеет физический смысл, если учесть формулу равновесия рычага, записанную выше. Оставим Архимеда и Землю в покое и решим несколько иную задачу, которая является не менее интересной.

Слона и муравья поместили на разные плечи рычага. Предположим, что центр масс слона находится в одном метре от опоры. На каком расстоянии от опоры должен находиться муравей, чтобы уравновесить слона?

Чтобы ответить на вопрос задачи, обратимся к табличным данным о массах рассматриваемых животных. Массу муравья возьмем 5 мг (5*10-6 кг), массу слона будем считать равной 5000 кг. Используя формулу равновесия рычага, получаем:

x = 5000/(5*10-6) = 109 м.

Муравей действительно может уравновесить слона, но для этого он должен располагаться от опоры рычага на расстоянии 1 миллион километров, что соответствует 1/150 расстояния от Земли до Солнца!

Задача с опорой на конце балки

Как было отмечено выше, у рычага опора под балкой может располагаться в любом месте. Предположим, что она находится вблизи одного из концов балки. Такой рычаг имеет единственное плечо, показанное ниже на рисунке.

Предположим, что груз (красная стрелка) имеет массу 50 кг и расположен точно посередине плеча рычага. Какой величины должна быть внешняя сила F (синяя стрелка), которая приложена к концу плеча, чтобы уравновесить этот груз?

Обозначим длину плеча рычага буквой d. Тогда можно записать условие равновесия в следующем виде:

F = m*g/2 = 50*9,81/2 = 245,25 Н

Таким образом, величина приложенной силы должна быть в два раза меньше веса груза.

Данный тип рычага используется в таких изобретениях, как ручная тачка для перемещения грузов или орехокол.

Источник

Характеристика понятия

Описываемое устройство является довольно простым. Но разбираясь в тонкостях правила рычага в физике, стоит отметить наличие у него нескольких составных частей:

Рычаг применяется для преобразования перемещения в силу и наоборот. Таким образом, удаётся добиться перераспределения выполняемой работы в пользу производимого перемещения или прикладываемой силы.

Если рассматривать строение человеческого скелета, можно прийти к выводу, что всем людям с самого рождения предоставляется способность пользоваться системой рычагов. При этом в роли механизма выступают плечи и предплечья.

Начало применения устройства с целью облегчения физической работы датируется древними временами. Имеются сведения, что ещё в Древнем Египте эти приборы шли в ход, когда люди поднимали из реки или колодца наполненный водой сосуд.

В 100 году до нашей эры была издана работа Плутарха под названием «Параллельные жизни». В ней говорится, что Архимеду удалось без посторонней помощи поднять над водой корабль, на борту которого на тот момент находились пассажиры и груз. Для этого были использованы блоки и рычаги. По сей день считается, что именно Архимед изобрёл механизм, поскольку самые древние сохранившиеся письменные работы, свидетельствующие о создании закона, принадлежат перу именно этого философа.

Момент силы

При изучении правила равновесия рычага следует отдельно разобраться в том, что значит единица измерения, называемая моментом силы (или крутящим моментом). Чтобы её изобразить с помощью формулы, необходимо умножить непосредственно величину силы (F) на плечо силы (d).

Схематически это будет изображаться так: М = d x F. Очень важное значение имеет ось вращения. Без её определения действующий момент силы лишён смысла. Использование величины М говорит о способности силы оборачивать систему вокруг оси. Применить её на практике можно на примере гайки, если постараться открутить последнюю без помощи гаечного ключа, а лишь одними руками. Тот же эффект будет наблюдаться и при попытке открыть дверь толчком около петель, а не за ручку.

При решении задач величина М способна приводить к вращению механизм как по ходу часовой стрелки, так и против него. При этом в первом случае момент отрицательный, а во втором — положительный.

Правило рычага

Чтобы разобраться, в чём заключается правило рычага, стоит рассмотреть пример работы классического механизма с двумя плечами и опорой, расположенной далеко от обоих концов доски. Во время применения прибора отмечается действие двух сил на него:

Обычно для создания F прикладываются человеческие усилия, а R определяется массой поднимаемого груза. Механизм достигнет равновесия лишь в том случае, если действующие на него моменты в сумме окажутся равны нулю. С учётом момента силы формулу для правила рычага можно записать так: R х DR — F х DF = 0, где D является плечом силы. F отрицательная из-за того, что стремится оборачивать плечо устройства по кругу в направлении движения часовой стрелки. Если записать формулу в виде равенства, она будет выглядеть так: R х DR = F х DF.

Отсюда следует, что для достижения простым рычагом равновесия достаточно добиться равенства моментов сил действия F и противодействия R. При применении механизма сохраняется энергия системы, свидетельствующая о необходимости проделывания определённой работы во время поднятия груза на какую-либо высоту.

Поскольку для получения значения правила рычага длину плеча умножают на силу, то существует возможность осуществления работы как с применением большей, так и меньшей силы. Но при первом варианте плечо механизма придётся установить на меньшую величину в вертикальном направлении, а второй случай предполагает перемещение плеча на большую величину. Эта особенность называется выигрышем и проигрышем в применении рычага.

Стоит отметить, что значения моментов никак не влияют на работу. Осуществление действия благодаря моменту силы отмечается лишь в тех случаях, когда система начинает поворачиваться на определённый угол по часовой стрелке.

Виды механизмов

Как известно, все рычаги подразделяются на три типа. Основывается эта классификация на относительном расположении опоры к силам R и F. Каждый из видов механизма стоит охарактеризовать отдельно:

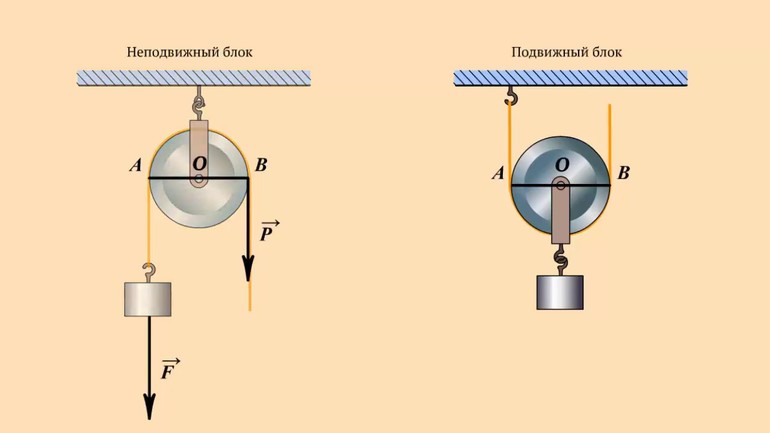
Помимо рычагов, при изучении правила равновесия стоит обратить внимание и на другой простой механизм, называемый блоком. Это цилиндр, оснащённый осью вращения и углублением, сформированным вдоль боковой поверхности. При его применении полностью отсутствует выигрыш в силе и пути, однако, благодаря использованию неподвижного блока, можно поменять направление воздействия F. К устройству применимо правило рычага, но только тогда, когда необходимо добиться выигрыша в силе для подвижных блоков, каждый из которых способен увеличить такое значение вдвое. Но при этом методе идентичная величина проигрывается в пути.

Пример решения задачи

В интернете существует масса приложений со встроенными онлайн-калькуляторами, позволяющими вычислить то или иное значение. Для решения задач по правилу рычага можно воспользоваться этими программами либо же научиться вычислять необходимые величины на основе примеров.

Итак, по условию задачи требуется узнать длину рычага, который позволит 50-килограммовой девушке поднять полуторатонный автомобиль, надавив на механизм всем весом. При этом точка опоры располагается в одном метре от края короткого плеча (D1), где D2 — длинное плечо.

Чтобы выяснить, во сколько раз механизм может дать выигрыш в силе, используется формула F/R=D1/D2. Обе силы оказывают воздействие на рычаг по разные стороны от его опоры, поэтому общая длина доски измеряется по формуле: D = D1+D2.

Согласно условию задачи, величина R, оказывающая действие на плечо D1, это вес автомобиля, обозначаемый Mg. При этом F представляет собой действующую на плечо D2 силу, являющуюся весом девушки (mg). Для получения длины рычага достаточно решить уравнение. Итак, в соответствии с вышеописанной формулой (mg/Mg = D1/D2), чтобы получить D2 необходимо произведение массы авто и длины короткого плеча разделить на вес девушки: (Mg x D1)/mg: D2 = (1500 кг х 1 м)/50 кг = 30 м. Чтобы получить общую длину рычага, понадобится сложить D2 и D1: 30м+1 м. Таким образом, искомая величина будет равна 31 метру.

В наши дни рычаги находят широкое применение как в быту, так и на производстве. Поэтому понимание принципа их работы очень важно практически для каждого человека.

Источник