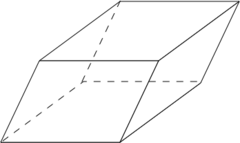
что такое правильный параллелепипед

Что такое параллелепипед: определение, элементы, виды, свойства

В данной публикации мы рассмотрим определение, элементы, виды и основные свойства параллелепипеда, в т.ч. прямоугольного. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение параллелепипеда

Параллелепипед – это геометрическая фигура в пространстве; шестигранник, гранями которого являются параллелограммы. Фигура имеет 12 ребер и 6 граней.

Параллелепипед – это разновидность призмы с параллелограммом в качестве оснований. Основные элементы фигуры те же, что и у призмы.

Примечание: Формулы для расчета площади поверхности (для прямоугольной фигуры) и объема параллелепипеда представлены в отдельных публикациях.

Виды параллелепипедов

Свойства параллелепипеда

1. Противоположные грани параллелепипеда взаимно параллельны и являются равными параллелограммами.

2. Все диагонали параллелепипеда пересекаются в одной точке и в ней делятся пополам.

3. Квадрат диагонали (d) прямоугольного параллелепипеда равен сумме квадратов трех его измерений: длины (a), ширины (b) и высоты (c).

d 2 = a 2 + b 2 + c 2

Примечание: к параллелепипеду, также, применимы свойства призмы.

Источник

Параллелепипед (ЕГЭ 2022)

Что за слово такое мудреное – «параллелепипед»? Что за многогранник скрывается за этим словом?

Что-то должно быть связано с параллельностью, не правда ли?

Читай статью, смотри вебинар и ты все про него будешь знать!

Параллелепипед — коротко о главном

Параллелепипед — это четырехугольная призма (многогранник с \( \displaystyle 6\) гранями), все грани которой — параллелограммы.

Прямой параллелепипед —это параллелепипед, у которого \( \displaystyle 4\) боковые грани — прямоугольники.

Прямоугольный параллелепипед — параллелепипед, у которого все грани — прямоугольники

Куб — параллелепипед, у которого все грани квадраты.

Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.

Свойства параллелепипеда

Параллелепипед — подробнее

Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.

Если слишком сложно, просто посмотри на картинку.

Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?

Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.

Далее смотри на картинки, запоминай и не путай!

Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.

Та грань, на которую опущена высота, называется основанием.

Свойства параллелепипеда

Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, а смежные.

Прямой параллелепипед

Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.

У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.

Прямоугольный параллелепипед

Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.

Это такая обувная коробка:

У прямоугольного параллелепипеда все грани – прямоугольники.

Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.

Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.\( \displaystyle <^<2>>=<^<2>>+<^<2>>+<^<2>>\).

Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.

Источник

Геометрические фигуры. Параллелепипед.

Параллелепипед — призма, основанием которой является параллелограмм либо (равносильно) многогранник с шестью гранями, являющимися параллелограммами. Шестигранник.

Параллелограммы, из которых состоит параллелепипед являются гранями этого параллелепипеда, стороны этих параллелограммов являются ребрами параллелепипеда, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда каждая грань является параллелограммом.

Как правило выделяют любые 2-е противолежащие грани и называют их основаниями параллелепипеда, а оставшиеся грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, которые не принадлежат основаниям являются боковыми ребрами.

2 грани параллелепипеда, которые имеют общее ребро являются смежными, а те, которые не имеют общих ребер — противоположными.

Отрезок, который соединяет 2 вершины, которые не принадлежат 1-ой грани является диагональю параллелепипеда.

Длины ребер прямоугольного параллелепипеда, которые не параллельны, являются линейными размерами (измерениями) параллелепипеда. У прямоугольного параллелепипеда 3 линейных размера.

Типы параллелепипеда.

Существует несколько видов параллелепипедов:

Прямым является параллелепипед с ребром, перпендикулярным плоскости основания.

Прямой параллелепипед с прямоугольником в основании является прямоугольным параллелепипедом. У прямоугольного параллелепипеда каждая из граней является прямоугольником.

Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, по отношению к основаниям, под углом, не равным 90 градусов.

Прямоугольный параллелепипед, у которого все 3 измерения имеют равную величину, является кубом. Каждая из граней куба – это равные квадраты.

Произвольный параллелепипед. Объём и соотношения в наклонном параллелепипеде в основном определяются при помощи векторной алгебры. Объём параллелепипеда равняется абсолютной величине смешанного произведения 3-х векторов, которые определяются 3-мя сторонами параллелепипеда (которые исходят из одной вершины). Соотношение между длинами сторон параллелепипеда и углами между ними показывает утверждение, что определитель Грама данных 3-х векторов равняется квадрату их смешанного произведения.

Свойства параллелепипеда.

В параллелепипед вписывают тетраэдр. Объем этого тетраэдра будет равняться третьей части объема параллелепипеда.

Источник

Параллелепипед

Параллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.

Содержание

Типы параллелепипеда

Различается несколько типов параллелепипедов:

Основные элементы

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Свойства

Основные формулы

Прямой параллелепипед

Площадь боковой поверхности S_б=Р_о*h, где Р_о — периметр основания, h — высота

Площадь полной поверхности S_п=S_б+2S_о, где S_о — площадь основания

Прямоугольный параллелепипед

Площадь боковой поверхности S_б=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда

Площадь полной поверхности S_п=2(ab+bc+ac)

Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

Площадь боковой поверхности S_б=4a², где а — ребро куба

Площадь полной поверхности S_п=6a²

Произвольный параллелепипед

В математическом анализе

В математическом анализе под n-мерным прямоугольным параллелепипедом понимают множество точек вида

Примечания

Ссылки

Полезное

Смотреть что такое «Параллелепипед» в других словарях:

ПАРАЛЛЕЛЕПИПЕД — греч., от parallelos., параллельный, и epidon, поверхность. Четырехсторонняя призма, у которой противоположные стороны параллельны между собой. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней.… … Словарь иностранных слов русского языка

Параллелепипед — Параллелепипед. ПАРАЛЛЕЛЕПИПЕД (от греческого parallelos параллельный и epipedon плоскость), призма, основание которой параллелограмм. … Иллюстрированный энциклопедический словарь

параллелепипед — призма, ромбоэдр, шестигранник Словарь русских синонимов. параллелепипед сущ., кол во синонимов: 4 • многогранник (38) • … Словарь синонимов

ПАРАЛЛЕЛЕПИПЕД — (от греч. parallelos параллельный и epipedon плоскость) призма, основанием которой служит параллелограмм … Большой Энциклопедический словарь

ПАРАЛЛЕЛЕПИПЕД — ПАРАЛЛЕЛЕПИПЕД, параллелепипеда, муж. (от греч. parallelos параллельный и epipedon поверхность) (мат.). Шестигранник, у которого противоположные грани равны и параллельны. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

ПАРАЛЛЕЛЕПИПЕД — ПАРАЛЛЕЛЕПИПЕД, а, муж. В математике: призма, основанием к рой служит параллелограмм. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

Параллелепипед — шестигранник, каждая пара противоположных гранейкоторого суть параллелограммы равной величины и параллельные междусобой … Энциклопедия Брокгауза и Ефрона

параллелепипед — а, м. parallélépipède m. <гр. parallelos + epidepon плоскость. геом. Шестигранник, сторонами которого являются параллелограммы. Крысин 1998. Цвет его <сапфира> лазуревой, сложение листоватое; представляет шести или многоугольную призьму … Исторический словарь галлицизмов русского языка

ПАРАЛЛЕЛЕПИПЕД — призма, основанием которой является (см.) … Большая политехническая энциклопедия

Параллелепипед — (греч. parallelepípedon, от parállelos параллельный и epípedon плоскость) шестигранник, противоположные грани которого попарно параллельны. П. имеет 8 вершин, 12 рёбер; его грани представляют собой попарно равные параллелограммы. П.… … Большая советская энциклопедия

Источник

Геометрические фигуры. Прямоугольный параллелепипед.

Примерами прямоугольного параллелепипеда являются спортивный зал, коробок спичек или системный блок компьютера.

Формулы прямоугольного параллелепипеда.

Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба являются равными квадратами.

Обозначим длину ребра куба как n, тогда площадь 1-ой грани:

Площадь поверхности куба:

У прямоугольного параллелепипеда есть еще одно измерение – объем параллелепипеда (обозначается как V).

Прямоугольники, которые составляют поверхность параллелепипеда, являются гранями параллелепипеда.

Прямоугольный параллелепипед определяют 3-мя измерениями:

Высота (обозначают как h) равняется длине ребра № 1.

Длина (обозначают как m) равняется длине ребра № 2.

Ширина (обозначают как n) равняется длине ребра № 3.

Площадь всей поверхности параллелепипеда обозначают как S:

S = (h • m + h • n + n • m) • 2

В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.

Площадь боковой поверхности:

где a, b — стороны основания,

c — боковое ребро прямоугольного параллелепипеда.

Источник

• ← что такое свободное пеленание фото пошаговое
• через сколько приходят деньги с налогового вычета за квартиру →

Многогранники
Правильные (Платоновы тела)	Трёхмерные Правильный тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр Четырёхмерные 6 правильных многогранников Большей размерности N-мерный куб • N-мерный октаэдр • N-мерный тетраэдр
Звёздчатый додекаэдр • Звёздчатый икосододекаэдр • Звёздчатый икосаэдр • Звёздчатый многогранник • Звёздчатый октаэдр
Выпуклые	Архимедовы тела Кубооктаэдр • Икосододекаэдр • Усечённый тетраэдр • Усечённый октаэдр • Усечённый икосаэдр • Усечённый куб • Усечённый додекаэдр • Ромбокубоктаэдр • Ромбоикосододекаэдр • Ромбоусечённый кубоктаэдр • Ромбоусечённый икосододекаэдр • Курносый куб • Курносый додекаэдр • Усечённый кубооктаэдр • Усечённый икосододекаэдр • Правильная призма • Антипризма Каталановы тела Ромбододекаэдр • Ромботриаконтаэдр • Триакистетраэдр • Тетракисгексаэдр • Пентакисдодекаэдр • Триакисоктаэдр • Триакисикосаэдр • Дельтоидальный икоситетраэдр • Дельтоидальный гексеконтаэдр •Пентагональный икоситетраэдр • Пентагональный гексеконтаэдр • Дисдакисдодекаэдр • Дисдакистриаконтаэдр Без полной пространственной симметрии Пирамида • Призма • Бипирамида • Антипризма • Зоноэдр • Параллелепипед • Ромбоэдр •Призматоид• Усечённая пирамида• Пентагондодекаэдр • Параллелоэдр
Формулы, теоремы, теории