Поток векторного поля

В математике поток векторного поля используется для двух различных понятий:

Поток векторного поля через поверхность

Поток векторного поля через поверхность — поверхностный интеграл первого рода по поверхности . По определению

где — векторное поле (вектор-функция векторного аргумента — точки пространства), — единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — то есть для дифференцируемой поверхности — так, чтобы было непрерывно; для неориентируемой поверхности это не важно, так как поток через неё всегда ноль), — элемент поверхности.

Иногда, особенно в физике, применяется обозначение

тогда поток записывается в виде

.

Физическая интерпретация

Пусть движение несжимаемой жидкости единичной плотности в пространстве задано векторным полем скорости течения . Тогда объем жидкости, который протечёт за единицу времени через поверхность , будет равен потоку векторного поля через поверхность .

См. также

Полезное

Смотреть что такое «Поток векторного поля» в других словарях:

Ротор векторного поля — Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной… … Википедия

ЛИНИИ ТОКА ВЕКТОРНОГО ПОЛЯ — линии, в каждой точке которых касательная имеет направление вектора поля в этой точке. Л. т. в. п. в гидродинамике это линия, в каждой точке которой касательная совпадает по направлению со скоростью частицы жидкости в данный момент времени.… … Словарь по гидрогеологии и инженерной геологии

Поток вектора — В математике поток векторного поля используется для двух различных понятий: 1. Поток векторного поля через гиперповерхность (см. ниже), 2. Поток векторного поля однопараметрическое семейство диффеоморфизмов Γt определямых дифференциальным… … Википедия

Поля теория — математическая теория, изучающая свойства скалярных, векторных (в общем случае тензорных) полей, т. е. областей пространства (или плоскости), каждой точке М которых поставлено в соответствие число u (М) (например, температура, давление,… … Большая советская энциклопедия

Поток — Поток: В Викисловаре есть статья «поток» Поток постоянное перемещение масс жидкости или газа в определённом направлении … Википедия

ПОТОК — векторного поля одно из понятий теории векторного поля. П. векторного поля а через поверхность дV выражается с точностью до знака поверхностным интегралом где п единичный вектор нормали к поверхности дV (предполагается, что изменение вектора ппо… … Математическая энциклопедия

Поток — векторного поля, одно из понятий теории поля. П. векторного поля через поверхность ∑ выражается с точностью до знака поверхностным интегралом где а = и n единичный вектор нормали к поверхности ∑… … Большая советская энциклопедия

Ротор поля — Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной… … Википедия

Оптический поток — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Оптический поток это изображение видимого движения объектов, поверхностей или краев сцены, получаемое в результате перемещения н … Википедия

Векторный потенциал электромагнитного поля — Классическая электродинамика … Википедия

Источник

Поток и циркуляция векторного поля

П о материалам лекции Ричарда Фейнмана

При описании законов электричества с точки зрения векторных полей, перед нами открываются две математически важные характеристики векторного поля: поток и циркуляция. Хорошо бы разобраться, что это за математические понятия и в чем заключается их практический смысл.

На вторую часть вопроса легко ответить сразу, ведь понятия потока и циркуляции лежат в основе уравнений Максвелла, на которых, по сути, и держится вся современная электродинамика.

Так, например, закон электромагнитной индукции может быть сформулирован следующим образом: циркуляция напряженности электрического поля E по замкнутому контуру C равна скорости изменения потока магнитного поля B через площадь поверхности S, ограниченной данным контуром С.

Далее мы достаточно просто, на понятных примерах с жидкостью, опишем то, как математически определяются, из чего берутся и получаются данные характеристики поля.

Поток векторного поля

Для начала давайте изобразим вокруг исследуемой области пространства некую замкнутую поверхность совершенно произвольной формы. После того как мы эту поверхность изобразим, зададимся вопросом, вытекает ли через данную замкнутую поверхность исследуемый объект, который мы именуем полем? Чтобы понять о чем здесь идет речь, рассмотрим простой пример с жидкостью.

Словосочетанием «поток векторного поля» (а для нашего примера более точным будет выражение «поток скорости жидкости») договоримся именовать общее количество воображаемой жидкости, которая именно вытекает наружу через поверхность из рассматриваемого объема, ограниченного данной замкнутой поверхностью (для потока скорости жидкости — сколько жидкости вытекает из объема за единицу времени).

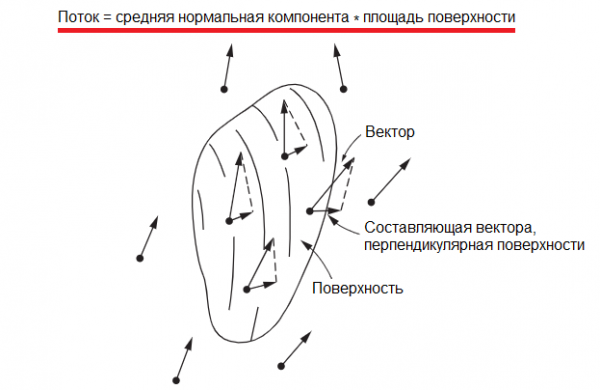
В результате, поток через элемент поверхности окажется равен произведению площади элемента поверхности на перпендикулярную составляющую скорости. Тогда общий (суммарный) поток через всю поверхность будет равен произведению средней нормальной составляющей скорости, которую будем отсчитывать изнутри наружу, на общую площадь поверхности.

Теперь вернемся к электрическому полю. Электрическое поле, конечно, нельзя считать скоростью течения какой-то жидкости, однако мы имеем право ввести математическое понятие потока, похожее на то, что мы описали выше как поток скорости жидкости.

Только в случае с электрическим полем, его поток может быть определен через среднюю нормальную компоненту напряженности электрического поля Е. Кроме того, поток электрического поля можно определить не обязательно через замкнутую поверхность, а через любую ограниченную поверхность, обладающую не равной нулю площадью S.

Циркуляция векторного поля

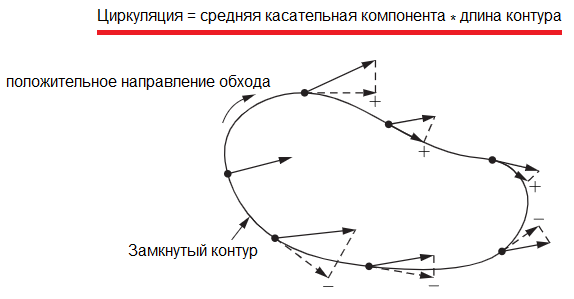
Всем хорошо известно, что поля можно для наглядности изображать в виде так называемых силовых линий, в каждой точке которых направление касательной совпадает с направлением напряженности поля.

Опять вернемся к аналогии с жидкостью и представим себе поле скоростей жидкости. Зададимся вопросом: циркулирует ли жидкость? То есть движется ли она преимущественно по направлению какого-то воображаемого замкнутого контура?

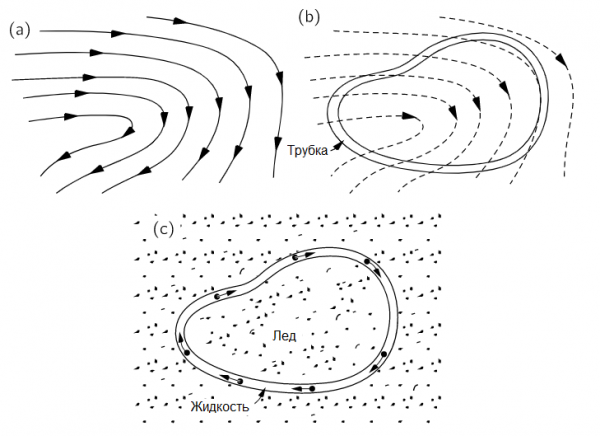
Для наглядности представим, что жидкость в неком большом сосуде как-то движется (рис a), и мы резко заморозили почти весь ее объем, но умудрились оставить не замороженным объем в форме ровной замкнутой трубки, в которой трение жидкости о стенки отсутствует (рис b).

За пределами этой трубки жидкость превратилась в лед, и поэтому больше не может двигаться, однако внутри трубки жидкость способна продолжить свое движение при условии что имеется преобладающий импульс, который гонит ее, например по часовой стрелке (рис c). Тогда произведение скорости жидкости в трубке на длину трубки мы и назовем циркуляцией скорости жидкости.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Ориентация поверхности. Поток векторного поля

Лекция 13. Ориентация поверхности. Поток векторного поля. Поверхностный интеграл второго рода, его свойства, физический смысл и вычисление. Связь поверхностных интегралов первого и второго рода.

Определим понятие стороны поверхности. Выберем на гладкой поверхности (замк-нутой или ограниченной гладким контуром) точку М0 и проведем в ней нормаль к поверхности, выбрав для нее определенное направление (одно из двух возможных). Проведем по поверхности замкнутый контур, начинающийся и заканчивающийся в точке М0. Рассмотрим точку М, обходящую этот контур, и в каждом из ее положений проведем нормаль того направления, в которое непрерывно переходит нормаль из предыдущей точки. Если после обхода контура нормаль вернется в точке М0 в перво-начальное положение при любом выборе точки М0 на поверхности, поверхность называется двусторонней. Если же направление нормали после обхода хотя бы одной точки изменится на противоположное, поверхность называется односторон-ней (примером односторонней поверхности служит лист Мебиуса).

Из вышесказанного следует, что выбор направления нормали в одной точке одно-значно определяет направление нормали во всех точках поверхности.

Определение 13.1. Совокупность всех точек поверхности с одинаковым направлени-ем нормали называется стороной поверхности.

Рассмотрим незамкнутую гладкую двустороннюю поверхность S, ограниченную контуром L, и выберем одну сторону этой поверхности.

Определение 13.2. Назовем положительным направление обхода контура L, при котором движение по контуру происходит против часовой стрелки относительно наблюдателя, находящегося в конечной точке нормали к какой-либо точке поверх-ности S, соответствующей выбранной стороне поверхности. Обратное направление обхода контура назовем отрицательным.

Поток векторного поля.

Рассмотрим векторное поле А(М), определенное в пространственной области G, ориентированную гладкую поверхность S G и поле единичных нормалей п(М) на выбранной стороне поверхности S.

Определение 13.3. Поверхностный интеграл 1-го рода

, (13.1)

где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.

Замечание 1. Если выбрать другую сторону поверхности, то нормаль, а, следова-тельно, и поток изменят знак.

Замечание 2. Если вектор А задает скорость течения жидкости в данной точке, то интеграл (13.1) определяет количество жидкости, протекающей в единицу времени через поверхность S в положительном направлении (отсюда общий термин «поток»).

Поверхностный интеграл второго рода.

Введем определение поверхностного интеграла 2-го рода по аналогии с соответ-ствующим криволинейным интегралом. Рассмотрим гладкую двустороннюю поверхность S, заданную уравнением z = z(x, y), в каждой точке которой определена функция f(M) = f(x, y, z), и выберем какую-либо из ее сторон (или, что то же самое, определенную ориентацию). Разобьем поверхность S на части S1, S2,…, Sп, выберем в каждой части Si точку Mi(xi, yi, zi), и умножим f(Mi) на площадь Di проекции части Si на плоскость Оху. При этом будем считать, проекция части верхней по отношению к плоскости Оху стороны рассматриваемой поверхности имеет знак «+», а нижней – знак «-». Составим сумму

. (13.2)

Определение 13.4. Если существует конечный предел суммы (13.2) при ρ→0, не зависящий от способа разбиения поверхности и выбора точек на ней, то он называет-ся поверхностным интегралом второго рода от функции f(M) по выбранной сто-роне поверхности S и обозначается

(13.3)

Замечание. В этой символической записи не содержится указания на то, какая сторона поверхности выбрана, поэтому это требуется оговаривать отдельно.

Подобным образом можно проектировать части поверхности на координатные плос-кости Оxz и Оyz (при условии, что уравнение поверхности можно представить в виде y = y(x, z) или x = x(y, z) ). Получим два других поверхностных интеграла 2-го рода:

и . (13.4)

Рассмотрев сумму интегралов вида (13.3) и (13.4) по одной и той же поверхности соответственно от функций P(x, y, z), Q(x, y, z), R(x, y, z), получим поверхностный интеграл второго рода общего вида:

(13.5)

Отметим основное свойство поверхностного интеграла 2-го рода:

При замене рассматриваемой стороны поверхности на противоположную поверхностный интеграл 2-го рода меняет знак: (13.6) Справедливость этого утверждения следует из определения 13.4.

Вычисление поверхностного интеграла 2-го рода.

Если задать единичный вектор выбранной нормали к поверхности S в виде п = , где α, β, γ – углы, образованные нормалью с осями координат, то (выбор знака зависит от направления нормали). Тогда из (13.2), (13.3) следует, что

. (13.7)

Здесь D – проекция поверхности S на плоскость Оху, а выражение для dS взято из формулы (12.5). Таким образом, вычисление поверхностного интеграла 2-го рода сводится к вычислению обычного двойного интеграла по области D от функции f, в которую вместо координаты z подставлено ее выражение из уравнения поверхности S. Обобщая эти рассуждения, получим, что

(13.8)

где D΄ и D΄΄ – проекции поверхности S на соответствующие координатные плоскости.

Пример. Вычислить поверхностный интеграл 2-го рода где S – нижняя сторона части конуса при

Применим формулу (13.7), учитывая, что выбрана нижняя сторона поверхности и что проекцией части конуса на плоскость Оху является круг :

Связь поверхностных интегралов первого и второго рода.

Учитывая, что проекции элемента поверхности Si на координатные плоскости имеют вид Sicosγ, Sicosβ, Sicosα, из (13.5) получим:

, (13.9)

где векторное поле , а – векторное поле единичных нормалей заданно-го направления в каждой точке поверхности. Следовательно, поверхностный интеграл 2-го рода (13.5) равен поверхностному интегралу 1-го рода (13.9). Эта формула предо-ставляет еще одну возможность вычисления поверхностного интеграла 2-го рода. Заметим, что при смене стороны поверхности меняют знак направляющие косинусы нормали, и, соответственно, интеграл в правой части равенства (13.9), который сам по себе, как поверхностный интеграл 1-го рода, от выбора стороны поверхности не зависит.

Пример. Рассмотрим интеграл , где S – внешняя сторона верхней половины сферы x² + y² + z² = R². Так как радиус сферы, проведенный в любую ее точку, можно считать нормалью к сфере в этой точке, единичный вектор нормали можно задать в виде п = . Тогда, используя формулу (13.9), получаем, что требуется вычислить поверхностный интеграл 1-го рода

(Область D – круг с центром в начале координат радиуса R).

Физический смысл поверхностного интеграла 2-го рода.

Сравнив формулы (13.9) и (13.1), увидим, что поверхностный интеграл 2-го рода представляет собой поток векторного поля через выбранную сторону поверхности S. При этом из формулы (13.9) следует, что поток можно задать и в виде поверхностного интеграла 1-го рода вида (13.5).

Источник