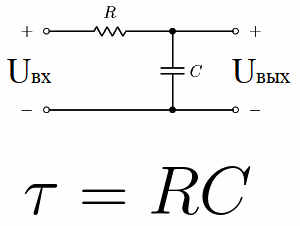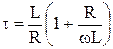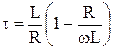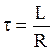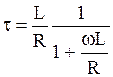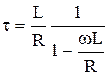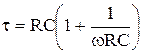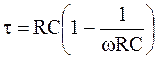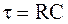что такое постоянная времени цепи

Природе свойственны периодические процессы: день сменяет ночь, теплое время года сменяется холодным и т. д. Период этих событий почти постоянен и поэтому может быть строго определен. Кроме того, мы вправе утверждать, что приведенные в качестве примера периодические природные процессы не являются затухающими, по крайней мере по отношению к продолжительности жизни одного человека.

Сплошь и рядом в электротехнике можно встретить так называемые экспоненциальные переходные процессы, суть которых заключается в том, что система просто стремится придти к какому-то равновесному состоянию, которое в конце концов выглядит как состояние покоя. Такой переходный процесс может быть как нарастающим, так и спадающим.

Внешняя сила сначала выводят динамическую систему из состояния равновесия, а затем не препятствует естественному возврату данной системы к ее исходному состоянию. Эта последняя фаза и есть так называемый переходный процесс, которому свойственна определенная длительность. Кроме того процесс выведения системы из равновесия также является переходным процессом с характерной длительностью.

Так или иначе, постоянной времени переходного процесса мы называем его временную характеристику, определяющую время, через которое некоторый параметр данного процесса изменится в «е» раз, то есть увеличится или уменьшится примерно в 2,718 раз по сравнению с состоянием, принятым за исходное.

Рассмотрим для примера электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Подобного рода цепь, где резистор включен последовательно с конденсатором, называется интегрирующей RC-цепью.

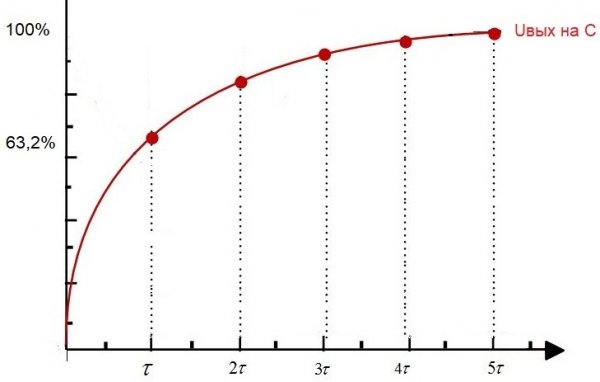
Если в начальный момент времени подать на такую цепь питание, то есть установить на входе некоторое постоянное напряжение Uвх, то Uвых — напряжение на конденсаторе, начнет по экспоненте нарастать.

Через время t1 напряжение на конденсаторе достигнет 63,2% от напряжения на входе. Так вот, промежуток времени от начального момента до t1 – это и будет постоянная времени данной RC-цепи.

Данную константу цепи называют «тау», она измеряется в секундах, а обозначают ее соответствующей греческой буквой. Численно для RC-цепи она равна R*C, где R выражается в омах, а С — в фарадах.

Интегрирующие RC-цепи применяются в электронике в качестве фильтров нижних частот, когда более высокие частоты необходимо отсечь (подавить), а более низкие — пропустить.

Практически механизм такой фильтрации зиждиться на следующем принципе. Для переменного тока конденсатор выступает как емкостное сопротивление, значение которого обратно пропорционально частоте, то есть чем выше частота — тем меньшим будет реактивное сопротивление конденсатора в омах.

Следовательно, если пропустить через RC-цепь переменный ток, то, как на плечах делителя напряжения, на конденсаторе упадет определенное напряжение, пропорциональное его емкостному сопротивлению на частоте пропускаемого тока.

Если известна частота среза и амплитуда входного переменного сигнала, то для разработчика не составит труда подобрать такие конденсатор и резистор в RC-цепь, чтобы минимальное (граничное) напряжение (для частоты среза — верхней частотной границы) приходилось на конденсатор как на реактивное сопротивление, входящее в состав делителя в совокупности с резистором.

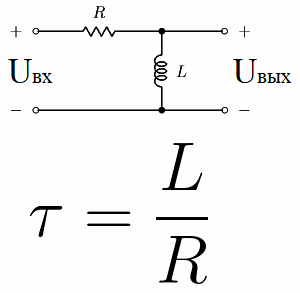
Теперь рассмотрим так называемую дифференцирующую цепь. Это цепь, состоящая из последовательно соединенных резистора и катушки индуктивности, RL-цепь. Ее постоянная времени численно равна L/R, где L – индуктивность катушки в генри, а R – сопротивление резистора в омах.

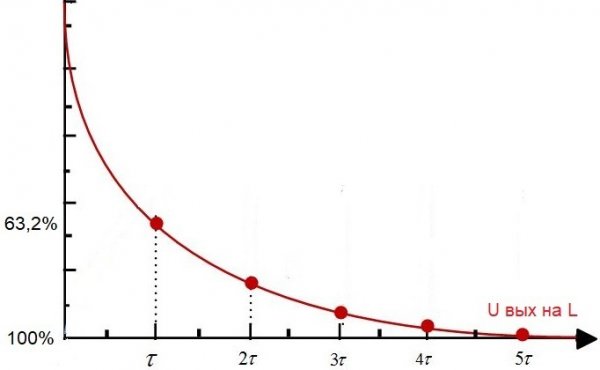
Если к такой цепи приложить постоянное напряжение от источника, то через время тау напряжение на катушке уменьшится по сравнению с U вх на 63,2%, то есть в полном соответствии со значением постоянной времени для данной электрической цепи.

В цепях переменного тока (переменных сигналов) LR-цепи применяются в качестве фильтров верхних частот, когда низкие частоты необходимо отсечь (подавить), а частоты выше (выше частоты среза — нижней частотной границы)— пропустить. Так вот, индуктивное сопротивление катушки тем больше, чем выше частота.

Как и в случае с рассмотренной выше RC-цепью, здесь используется принцип делителя напряжения. Ток более высокой частоты, пропускаемый через RL-цепь, вызовет большее падение напряжения на индуктивности L, как на индуктивном сопротивлении, входящем в состав делителя напряжения в совокупности с резистором. Задача разработчика — подобрать такие R и L, чтобы минимальное (граничное) напряжение на катушке получалось как раз на частоте среза.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Источник

14. Постоянная времени RC-цепи

ЭКСПЕРИМЕНТ 14 Постоянная времени RC-цепи

После проведения данного эксперимента Вы сможете продемонстрировать, как величины емкости и сопротивления управляют временем заряда и разряда конденсатора.

* Источник постоянного напряжения

* Секундомер или часы с секундной стрелкой

один электролитический конденсатор 22 мкФ, один электролитический конденсатор 100 мкФ, один резистор 33 кОм, 1/4 Вт,

* один резистор 100 кОм, 1/4 Вт, один резистор 220 кОм, 1/4 Вт, один резистор 1 МОм, 1/4 Вт.

Конденсатор представляет собой электроэлемент, который накапливает электричество в форме электрического поля. Когда к конденсатору прикладывается постоянное напряжение, электроны покидают одну обкладку конденсатора и скапливаются на другой обкладке под действием

внешней силы напряжения. Это приводит к заряду конденсатора до напряжения, равного приложенному напряжению.

Положительный заряд на одной обкладке конденсатора и отрицательный заряд на другой обкладке конденсатора создают сильное электрическое поле между обкладками в диэлектрике. Такой заряд удерживается даже в том случае, если источник напряжения отсоединяется. Конденсатор может разряжаться соединением его выводов друг с другом для нейтрализации заряда на обкладках.

Зарядка и разрядка конденсатора до определенного напряжения занимает конечный период времени (называемый постоянной времени); это время зависит в основном от емкости конденсатора и включенного последовательно сопротивления. Постоянная времени зарядки — это время, которое требуется конденсатору, чтобы зарядиться до 63, 2% приложенного напряжения. Это время (Т) в секундах выражается так:

Постоянная времени разрядки — это время, которое требуется конденсатору, чтобы разрядиться до 36, 8% от начального заряда.

Время, которое требуется конденсатору, чтобы полностью зарядиться до приложенного напряжения или полностью разрядиться до нуля, приблизительно равно пятикратной постоянной времени, то есть 5Т.

Многие электронные схемы основываются на идее использования постоянной времени для своей работы. К таким схемам относятся, например, схемы задержки времени, схемы формирования импульсов и сигналов, а также генераторные схемы. В настоящем эксперименте Вы познакомитесь с постоянной времени заряда и разряда, используя для этого три различных группы резисторов и конденсаторов.

Резистор 100 кОм; конденсатор 100 мкф

1. Соберите схему, показанную на рисунке 14-1. Соблюдайте полярность при подключении электролитического конденсатора.

2. Отрегулируйте источник питания на напряжение 12 В.

3. Рассчитайте величину напряжения, которое появится на конденсаторе в течение одной постоянной времени.

Напряжение (Т) = ______ В

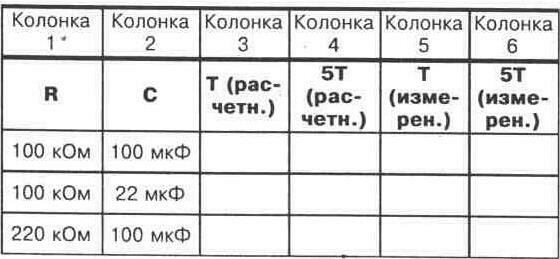
4. Рассчитайте постоянную времени, используя значения, показанные на рисунке 14-1. Запишите Ваш результат в колонку 3 на рисунке 14-2. Рассчитайте также значение времени, которое потребуется конденсатору, чтобы полностью зарядиться (5Т). Запишите Ваш результат в колонку 4 на рисунке 14-2.

5. Соедините измерительные выводы Вашего мультиметра, соблюдая полярность, с выводами конденсатора. Мультиметр должен показать 0 В. Если это не так, на обкладках конденсатора имеется некоторое остаточное напряжение. Удалите его, кратковременно закорачивая выводы конденсатора друг с другом в течение нескольких секунд. Снова выполните измерение напряжения Вашим мультиметром, чтобы убедиться, что напряжение конденсатора равно нулю.

6. Оставьте измерительные выводы мультиметра на выводах конденсатора, свободный конец резистора 100 кОм присоедините к выводу+ 12 В источника питания. В момент присоединения

запустите Ваш секундомер или начните отсчет времени при помощи секундной стрелки Ваших часов. Когда напряжение на конденсаторе начнет расти, замечайте его величину. Когда напряжение на конденсаторе достигнет значения, которое Вы рассчитали в шаге 2, заметьте время по секундомеру или по секундной стрелке. Запишите это значение в качестве измеренной постоянной времени в колонку 5 рисунка 14-2.

ПРИМЕЧАНИЕ: Повторите данный шаг несколько раз, чтобы убедиться в том, что Ваш отсчет времени относительно точен. Ведь Вы пытаетесь наблюдать как за показаниями вольтметра, так и за секундомером, чтобы определить время, необходимое для достижения конкретного уровня напряжения. Это довольно мудреная операция, так что повторите ее несколько раз для большей точности измерений. ВНИМАНИЕ:

если Вам потребуется повторять эксперимент, удаляйте резистор 10кОм и полностью разряжайте конденсатор 100 мкФ, прежде чем приступать к каждому дополнительному измерению. 7. Снова полностью разрядите конденсатор и снова подсоедините измерительные выводы. Коснитесь свободным выводом резистора 100 кОм к выводу +12 В источника питания. На этот раз измерьте время, которое потребуется конденсатору для полной зарядки до величины приложенного напряжения, которое Вы измерили в шаге 1. Как и прежде, начните отсчет времени по секундомеру или по секундной стрелке часов в том момент, когда Вы подаете напряжение на резистор. Запишите это измеренное время,

которое требуется конденсатору для полной зарядки, в колонку 6 рисунка 14-2.

Резистор 11 к0м; конденсатор 22 мкф

8. Повторите шаги с 4 по 7. используя конденсатор 22 мкф и резистор 100 к0м. Заполните поля в таблице на рисунке 14-2, как Вы это делали раньше. Вашими расчетными и измеренными значениями.

Резистор 220 к0м; конденсатор 100 мкф

9. Снова повторите шаги с 4 по 7, но на этот раз используйте конденсатор 100 мкФ и резистор 220 к0м. Запишите Ваши расчетные и измеренные значения в таблицу на рисунке 14-2.

10. Рассматривая информацию на рисунке 14-2 и замечая различные значения времени, полученные при различных значениях сопротивления и емкости, сделайте Ваше собственное заключение относительно влияния значений сопротивления и емкости на постоянную времени.

Резистор 100 к0м; конденсатор 100 мкф

11. Перекомпонуйте схему, чтобы она соответствовала схеме, показанной на рисунке 14-3. Соблюдайте полярность при подключении электролитического конденсатора. В данной части эксперимента Вы будете демонстрировать процесс разрядки конденсатора. Чтобы сделать это, подключите резистор параллельно конденсатору.

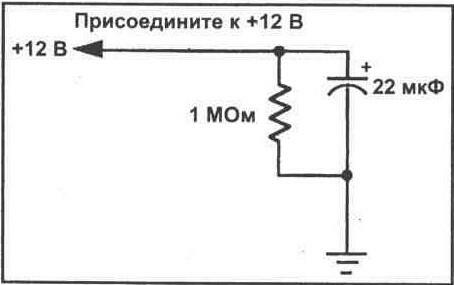
12. Рассчитайте постоянную времени схемы и время, которое требуется для полной разрядки конденсатора, и запишите Ваши данные в колонку 3 на рисунке 14-4.

13. Далее определите величину напряжения, до которого разрядится конденсатор за одну постоянную времени. Используйте исходное напряжение

источника питания, которое Вы измерили в шаге 1. Рассчитайте величину напряжения, которое будет присутствовать на Конденсаторе после его разрядки в течение одной постоянной времени.

Напряжение (t) = _______ В

Резистор 100 кОм; конденсатор 22 мкф

14. Подключите измерительные выводы Вашего мультиметра к конденсатору 22 мкф. В данное время напряжение должно равняться нулю, поскольку любой заряд на обкладках конденсатора был устранен в процессе разрядки конденсатора через резистор 1 МОм. Подключите схему к выводу+ 12 В источника питания. Конденсатор заряжается немедленно до напряжения источника питания; последовательно с конденсатором нет подключенного сопротивления.

15. Продолжайте фиксировать измерительные выводы мультиметра параллельно выводам конденсатора. Удалите соединительный провод с вывода+ 12 В источника питания. Одновременно с удалением провода начните отсчет времени по Вашему секундомеру или по секундной стрелке часов. Наблюдайте при этом за напряжением на выводах конденсатора. Когда напряжение достигнет нужного значения, заметьте время. Запишите постоянную времени в колонку 5 таблицы на рисунке 14-4. Как и раньше. Вы можете пожелать повторить шаги 13 и 14 несколько раз, чтобы улучшить точность измерений. Ведь, поскольку Вам приходится наблюдать одновременно за двумя значениями, измерение довольно хитроумно. Усредняя несколько показаний, Вы получите большую точность в измерении.

Резистор 220 кОм; конденсатор 22 мкф

16. Снова повторите шаги с 12 по 15, но на этот раз используйте конденсатор 22 мкф и резистор 220 кОм. Снова рассчитайте значения времени разрядки для одной постоянной времени и для пяти постоянных времени. Запишите все Ваши данные в таблицу на рисунке 14-4.

17. Рассматривая информацию на рисунке 14-4 и замечая различные значения времени, полученные при различных значениях сопротивления и емкости, сделайте Ваше заключение относительно зависимости между временем разрядки и значениями сопротивления и емкости.

18. На основании сравнения Ваших расчетных и измеренных значений объясните возможные несоответствия.

1. Требуется то же самое время для полной зарядки конденсатора, какое требуется и для полной его разрядки:

а) высказывание истинно,

б) высказывание ложно.

. 2. До какого напряжения зарядится конденсатор 5 мкф через резистор 10кОм за одну постоянную времени при его подключении к источнику питания 6 В?

3. Сколько времени потребуется конденсатору из вопроса 2, чтобы полностью разрядиться?

4. Конденсатору требуется 80 миллисекунд, чтобы полностью зарядиться. Поэтому постоянная времени равна:

5. При заданных значениях R (сопротивление) и С (емкость) емкость удваивается, а сопротивление уменьшается в два раза, при этом постоянная времени:

Источник

Содержание

Частота среза

или, что то же самое,

где сопротивление в омах и емкость в фарадах дают постоянную времени в секундах или частоту в Гц.

f _c в Гц = 159155 / τ в мкс τ в мкс = 159155 / f _c в Гц

Другие полезные уравнения:

В более сложных схемах, состоящих из более чем одного резистора и / или конденсатора, метод постоянной времени холостого хода обеспечивает способ аппроксимации частоты среза путем вычисления суммы нескольких постоянных времени RC.

Задержка

Типичная задержка цифрового распространения резистивного провода составляет примерно половину R, умноженного на C; так как R и C пропорциональны длине провода, задержка масштабируется как квадрат длины провода. Заряд распространяется путем диффузии в таком проводе, как объяснил лорд Кельвин в середине девятнадцатого века. До тех пор, пока Хевисайд не обнаружил, что уравнения Максвелла подразумевают распространение волн при наличии достаточной индуктивности в цепи, считалось, что это квадратное соотношение диффузии является фундаментальным ограничением для улучшения телеграфных кабелей дальней связи. Этот старый анализ был заменен в области телеграфа, но остается актуальным для длительных межсоединений на кристалле.

Источник

СОДЕРЖАНИЕ

Дифференциальное уравнение

Системы LTI первого порядка характеризуются дифференциальным уравнением

где τ представляет собой экспоненциальную константу затухания, а V является функцией времени t

Пример решения

Пример решения дифференциального уравнения с начальным значением V ₀ и без функции принуждения:

Обсуждение

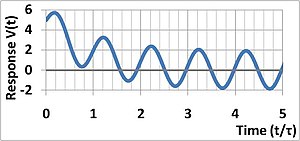
Такое поведение называется «убывающей» экспоненциальной функцией. Время τ (тау) называется «постоянной времени» и может использоваться (как в этом случае), чтобы указать, насколько быстро затухает экспоненциальная функция.

t = время (обычно t > 0 в технике управления) V ₀ = начальное значение (см. «Особые случаи» ниже).

Конкретные случаи

Связь постоянной времени с полосой пропускания

Предположим, что функция принуждения выбрана синусоидальной, поэтому:

В течение долгого времени убывающие экспоненты становятся незначительными, и стационарное решение или долгосрочное решение:

Величина этого ответа:

Обозначение f _3dB происходит от выражения мощности в децибелах и наблюдения, что половинная мощность соответствует уменьшению значения | V _∞ | в 1 / √2 раз или на 3 децибела.

Таким образом, постоянная времени определяет полосу пропускания этой системы.

Переходная характеристика с произвольными начальными условиями

Предположим, что функция принуждения выбрана в качестве пошагового входа, поэтому:

с u ( t ) ступенчатой ​​функцией Хевисайда. Общее решение этого уравнения для времен t ≥ 0 с при условии, что V ( t = 0) = V ₀ :

(Можно заметить, что этот отклик является пределом ω → 0 вышеупомянутого отклика на синусоидальный вход.)

Долгосрочное решение не зависит от времени и от начальных условий:

Постоянная времени остается неизменной для одной и той же системы независимо от условий запуска. Проще говоря, система приближается к своей конечной устойчивой ситуации с постоянной скоростью, независимо от того, насколько она близка к этому значению в любой произвольной начальной точке.

Например, рассмотрим электродвигатель, запуск которого хорошо моделируется системой LTI первого порядка. Предположим, что при запуске из состояния покоя двигатель принимает 1 / 8 секунды, чтобы достичь 63% номинальной скорости 100 об / мин, или 63 об / мин, то есть меньше 37 об / мин. Тогда окажется, что после следующего 1 / 8 секунды двигатель увеличил скорость на 23 об / мин, что составляет 63% от этой разницы в 37 об / мин. Это доводит его до 86 об / мин, что все еще составляет 14 об / мин. После третьего 1 / 8 секунды, двигатель будет набирать дополнительные 9 об / мин (63% от этой разницы в 14 об / мин), что означает 95 об / мин.

Фактически, при любой начальной скорости s ≤ 100 об / мин, 1 / 8 секунды спустя этот конкретный двигатель получит дополнительные 0,63 × (100 с ) об / мин.

Примеры

Постоянные времени в электрических цепях

Электрические цепи часто более сложны, чем эти примеры, и могут иметь несколько постоянных времени (см. Некоторые примеры в разделе « Переходная характеристика» и « Разделение полюсов»). В случае наличия обратной связи в системе могут наблюдаться нестабильные возрастающие колебания. Кроме того, физические электрические цепи редко являются действительно линейными системами, за исключением возбуждений с очень низкой амплитудой; однако широко используется приближение линейности.

Тепловая постоянная времени

где ρ = плотность, с _р = удельная теплоемкость и V представляет собой объем тела. Отрицательный знак указывает на падение температуры, когда теплоотвод идет наружу от тела (то есть, когда F > 0). Приравнивая эти два выражения для теплопередачи,

Очевидно, это LTI-система первого порядка, которую можно представить в виде:

Другими словами, постоянная времени говорит о том, что большие массы ρV и большая теплоемкость c _p приводят к более медленным изменениям температуры, в то время как большие площади поверхности A _s и лучшая теплопередача h приводят к более быстрым изменениям температуры.

Константы времени в нейробиологии

Постоянная времени используется для описания роста и падения мембранного напряжения, где рост описывается выражением

и падение описывается

V Максимум знак равно р м я <\ displaystyle V _ <\ textrm > = r_ I>

Экспоненциальный спад

Метеорологические датчики

Чаще всего это относится к измерениям температуры, температуры точки росы, влажности и давления воздуха. Особенно страдают радиозонды из-за их быстрого увеличения высоты.

Источник

В классическом методе анализа переходных процессов независимые начальные условия учитываются

1) введением в операторную схему замещения внутренних э. д. с.

2)+ при определении постоянных интегрирования

Постоянная времени цепи это время

1) переходного процесса

2) за которое свободная составляющая переменной уменьшается в “e” раз

3)+? за которое свободная составляющая переменной уменьшается в “e 2 ” раз

Постоянная времени цепи, состоящей из индуктивности и сопротивления

1)

2)

3) +

4)

5)

Постоянная времени цепи, состоящей из емкости и сопротивления

1)

2)

3) +

Постоянная времени цепи зависит от

1) +схемы цепи и параметров ее элементов

2) формы напряжений и токов источников

3) амплитуды напряжений и токов источников

С увеличением постоянной времени цепи время переходного процесса

С уменьшением постоянной времени цепи время переходного Процесса

В цепи с сопротивлением индуктивностью и емкостью заряд-разряд емкости апериодический, если сопротивление по сравнению с критическим сопротивлением

В цепи с сопротивлением индуктивностью и емкостью заряд-разряд емкости критический, если сопротивление по сравнению с критическим сопротивлением

В цепи с сопротивлением индуктивностью и емкостью заряд-разряд емкости колебательный, если сопротивление по сравнению с критическим сопротивлением

При использовании для приближенного дифференцирования сигналов цепи, состоящей из последовательного соединения сопротивления и индуктивности выходное напряжение снимается с

3) цепь не выполняет эту операцию

При использовании для приближенного интегрирования сигналов цепи, состоящей из последовательного соединения сопротивления и индуктивности выходное напряжение снимается с

3) цепь не выполняет эту операцию

При использовании для приближенного дифференцирования сигналов цепи, состоящей из последовательного соединения сопротивления и емкости выходное напряжение снимается с

3) цепь не выполняет эту операцию

При использовании для приближенного интегрирования сигналов цепи, состоящей из последовательного соединения сопротивления и емкости выходное напряжение снимается с

3) цепь не выполняет эту операцию

При использовании пассивной цепи для дифференцирования сигналов с увеличением постоянной времени цепи точность дифференцирования

2) остается без изменения

При использовании пассивной цепи для дифференцирования сигналов с уменьшением постоянной времени цепи точность дифференцирования

2) остается без изменения

При использовании пассивной цепи для интегрирования сигналов с увеличением постоянной времени цепи точность интегрирования

2) остается без изменения

При использовании пассивной цепи для интегрирования сигналов с уменьшением постоянной времени цепи точность интегрирования

2) остается без изменения

При использовании для дифференцирования сигналов активных RC-цепей на базе операционных усилителей точность дифференцирования зависит от

3) постоянной времени цепи

4)+ коэффициента усиления операционного усилителя

При использовании для интегрирования сигналов активных RC-цепей на базе операционных усилителей точность интегрирования зависит от

3) постоянной времени цепи

4+коэффициента усиления операционного усилителя

Переменные состояния цепи это

1)+ токи в индуктивностях, напряжения на емкостях

2) напряжения на индуктивностях, токи в емкостях

Источник