что такое постоянная функция

Какие свойства элементарных функций?

Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.

Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.

Постоянная функция

Выделяют следующие виды основных элементарных функций:

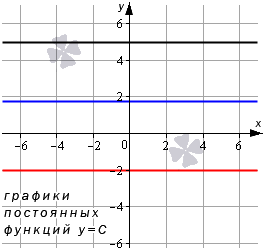
Постоянная функция определяется формулой: y=C (C – некое действительное число) и имеет также название: константа. Данная функция определяет соответствие любому действительному значению независимой переменной x одного и того же значения переменной y – значение C.

График константы – это прямая, которая параллельна оси абсцисс и проходит через точку, имеющую координаты (0, С). Для наглядности приведем графики постоянных функций y=5, y=-2, y=3, y=3 (на чертеже обозначено черным, красным и синим цветами соответственно).

Свойства постоянных функций:

Корень n-й степени

Данная элементарная функция определяется формулой y=xn (n – натуральное число больше единицы).

Рассмотрим две вариации функции.

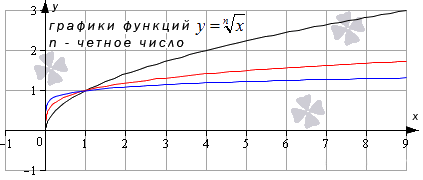
Корень n-й степени, n – четное число

Похожий вид у графиков функции четной степени при иных значениях показателя.

Свойства функции корень n-ой степени, n – четное число

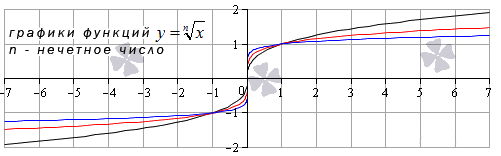
Такая функция определена на всем множестве действительных чисел. Для наглядности рассмотрим графики функций y=x3, y=x5 и x9. На чертеже они обозначены цветами: черный, красный и синий цвета кривых соответственно.

Иные нечетные значения показателя корня функции y=xn дадут график аналогичного вида.

Свойства функции корень n-ой степени, n – нечетное число

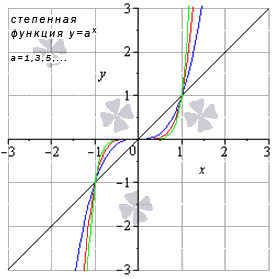
Степенная функция

Степенная функция определяется формулой y=xa. Вид графиков и свойства функции зависят от значения показателя степени.

Источник

Постоянная функция: характеристики, примеры, упражнения

Содержание:

В постоянная функция тот, в котором значение y остается постоянным. Другими словами: постоянная функция всегда имеет видf (x) = k, где k это действительное число.

При построении постоянной функции в системе координат ху, всегда получается прямая линия, параллельная горизонтальной оси или оси Икс.

Эта функция является частным случаем аффинная функция, график которой также представляет собой прямую линию, но с наклоном. Постоянная функция имеет нулевой наклон, то есть это горизонтальная линия, как видно на рисунке 1.

Есть график трех постоянных функций:

Постоянные функциональные характеристики

Мы можем резюмировать основные характеристики постоянной функции следующим образом:

-Его график представляет собой горизонтальную прямую линию.

-Он имеет единственное пересечение с осью Yчто стоит k.

Примеры

Функции необходимы для установления связей между величинами, которые каким-то образом зависят друг от друга. Отношения между ними можно смоделировать математически, чтобы выяснить, как один из них ведет себя при изменении другого.

Это помогает создавать модели для многих ситуаций и делать прогнозы относительно их поведения и эволюции.

Несмотря на кажущуюся простоту, постоянная функция имеет множество приложений. Например, когда дело доходит до изучения величин, которые остаются постоянными с течением времени или, по крайней мере, в течение значительного времени.

Таким образом, величины ведут себя в следующих ситуациях:

-The скорость крейсерская машина, едущая по длинной прямой дороге. Пока вы не тормозите и не ускоряетесь, автомобиль движется равномерно по прямой.

-Полностью заряженный конденсатор, отключенный от цепи, имеет грузить постоянная во времени.

-Наконец, парковка с фиксированной ставкой, поддерживает цена постоянно, независимо от того, как долго там стоит машина.

Другой способ представления постоянной функции

В качестве альтернативы постоянная функция может быть представлена ​​следующим образом:

Поскольку любое значение Икс поднятие до 0 дает в результате 1, предыдущее выражение сводится к уже знакомому:

Конечно, это происходит до тех пор, пока значение k отличается от 0.

Поэтому постоянная функция также классифицируется как полиномиальная функция степени 0, поскольку показатель степени переменной Икс равно 0.

Решенные упражнения

— Упражнение 1

Ответьте на следующие вопросы:

а) Можно ли утверждать, что линия, заданная x = 4, является постоянной функцией? Обоснуйте свой ответ.

б) Может ли постоянная функция иметь точку пересечения по оси x?

Ответ на

Вот график прямой x = 4:

Ответ б

Обычно постоянная функция не пересекается с осью Икс, если это не у = 0, в этом случае это ось Икс Правильно сказано.

Ответ c

Да, так как ш постоянна, как и его квадрат. Важно то, что ш не зависят от входной переменной Икс.

— Упражнение 2.

Решение

Чтобы найти пересечение между этими двумя функциями, их можно соответственно переписать как:

Их уравнивают, получая:

Что такое линейное уравнение первой степени, решение которого:

— Упражнение 3.

Покажите, что производная постоянной функции равна 0.

Решение

Из определения производной имеем:

Подставляя в определение:

Кроме того, если мы подумаем о производной как о скорости изменения dy / dx, постоянная функция не претерпевает никаких изменений, поэтому ее производная равна нулю.

— Упражнение 4.

Найдите неопределенный интеграл от f (x) = k.

Решение

Компания сотовой связи предлагает безлимитный доступ в Интернет по фиксированной ставке за 15 долларов в месяц. Какова функция цены во времени?

Решение

— Упражнение 6

Следующий график зависимости скорости от времени соответствует движению частицы.

а) Напишите выражение для функции скорости как функции времени v (t).

б) Найдите расстояние, пройденное мобильным телефоном за интервал времени от 0 до 9 секунд.

Решение для

Из представленного графика видно, что:

–v = 2 м / с в интервале времени от 0 до 3 секунд

-Мобильный телефон останавливается между 3 и 5 секундами, так как в этом интервале скорость равна 0.

Это пример кусочной функции или кусочной функции, которая, в свою очередь, состоит из постоянных функций, действительных только для указанных временных интервалов. Сделан вывод, что искомая функция:

Решение б

По графику v (t) можно рассчитать пройденное мобильным устройством расстояние, которое численно эквивалентно площади под кривой или на ней. Таким образом:

-Расстояние от 0 до 3 секунд = 2 м / с. 3 с = 6 м

— От 3 до 5 секунд его задержали, поэтому он не ехал на какое-то расстояние.

-Расстояние от 5 до 9 секунд = 3 м / с. 4 с = 12 м

Всего мобиль проехал 18 м. Обратите внимание, что хотя скорость отрицательна в интервале от 5 до 9 секунд, пройденное расстояние положительно. Что происходит, так это то, что за этот промежуток времени мобильный телефон изменил представление о своей скорости.

Ссылки

Кошмары и ночные кошмары: различия и сходства

Флувоксамин: способы применения, меры предосторожности и побочные эффекты этого препарата

Источник

Основные элементарные функции: их свойства и графики

Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.

Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.

Выделяют следующие виды основных элементарных функций:

Постоянная функция

Свойства постоянных функций:

Корень n-й степени

Данная элементарная функция определяется формулой y = x n ( n – натуральное число больше единицы).

Рассмотрим две вариации функции.

Похожий вид у графиков функции четной степени при иных значениях показателя.

Свойства функции корень n-ой степени, n – четное число

Иные нечетные значения показателя корня функции y = x n дадут график аналогичного вида.

Свойства функции корень n-ой степени, n – нечетное число

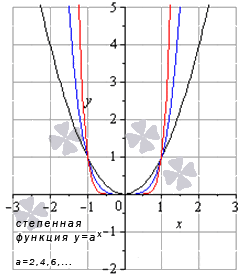
Степенная функция

Вид графиков и свойства функции зависят от значения показателя степени.

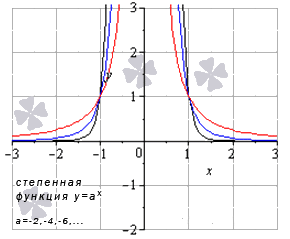
Степенная функция при нечетном положительном показателе

Свойства степенной функции, когда показатель степени – нечетный положительный

Степенная функция при четном положительном показателе

Свойства степенной функции, когда показатель степени – четный положительный:

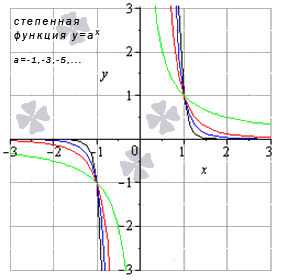
Степенная функция при нечетном отрицательном показателе

Свойства степенной функции, когда показатель степени – нечетный отрицательный:

Степенная функция при четном отрицательном показателе степени

Свойства степенной функции, когда показатель степени – четный отрицательный:

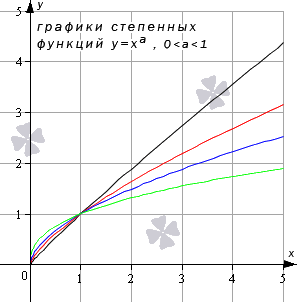
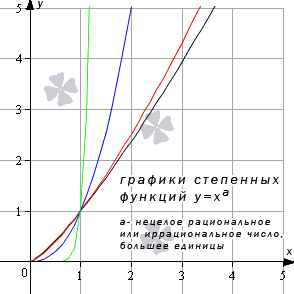
Степенная функция при рациональном или иррациональном показателе (значение больше нуля и меньше единицы)

Иные значения показателя степени a (при условии 0 a 1 ) дадут аналогичный вид графика.

Свойства степенной функции при 0 a 1 :

Степенная функция при нецелом рациональном или иррациональном показателе степени (больше единицы)

Иные значения показателя степени а при условии a > 1 дадут похожий вид графика.

Свойства степенной функции при a > 1 :

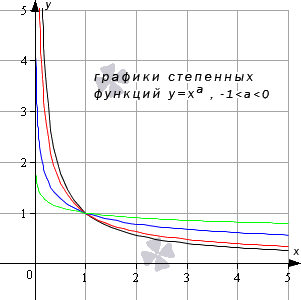
Степенная функция при действительном показателе степени (больше минус единицы и меньше нуля)

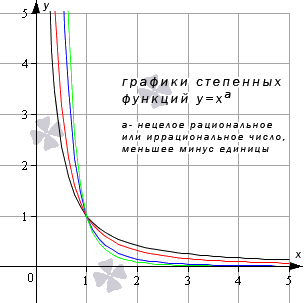
Степенная функция при нецелом действительном показателе степени (меньше минус единицы)

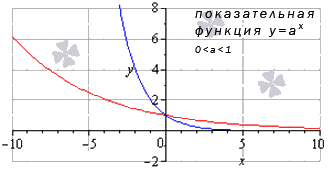
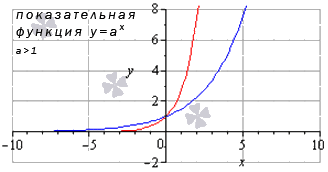
Показательная функция

Сначала разберем ситуацию, когда основание показательной функции имеет значение от нуля до единицы ( 0 a 1 ) . Наглядным примером послужат графики функций при a = 1 2 (синий цвет кривой) и a = 5 6 (красный цвет кривой).

Свойства показательной функции, когда основание меньше единицы:

Проиллюстрируем этот частный случай графиком показательных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет графика).

Иные значения основания, большие единицы, дадут аналогичный вид графика показательной функции.

Свойства показательной функции, когда основание больше единицы:

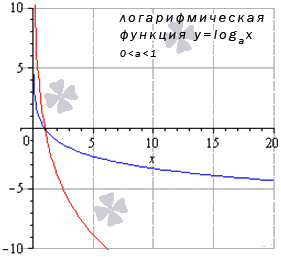
Логарифмическая функция

График логарифмической функции имеет различный вид, исходя из значения основания а.

Иные значения основания, не большие единицы, дадут аналогичный вид графика.

Свойства логарифмической функции, когда основание меньше единицы:

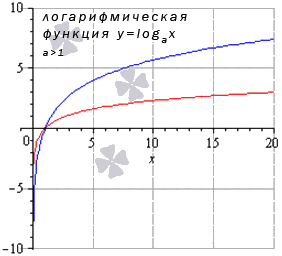
Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а > 1 . На чертеже ниже – графики логарифмических функций y = log 3 2 x и y = ln x (синий и красный цвета графиков соответственно).

Иные значения основания больше единицы дадут аналогичный вид графика.

Свойства логарифмической функции, когда основание больше единицы:

Тригонометрические функции, их свойства и графики

Тригонометрические функции – это синус, косинус, тангенс и котангенс. Разберем свойства каждой из них и соответствующие графики.

В общем для всех тригонометрических функций характерно свойство периодичности, т.е. когда значения функций повторяются при разных значениях аргумента, отличающихся друг от друга на величину периода f ( x + T ) = f ( x ) ( T – период). Таким образом, в списке свойств тригонометрических функций добавляется пункт «наименьший положительный период». Помимо этого, будем указывать такие значения аргумента, при которых соответствующая функция обращается в нуль.

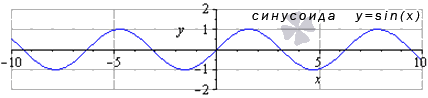
График данной функции называется синусоида.

Свойства функции синус:

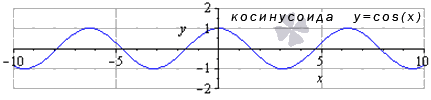
График данной функции называется косинусоида.

Свойства функции косинус:

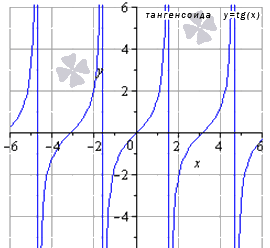
График данной функции называется тангенсоида.

Свойства функции тангенс:

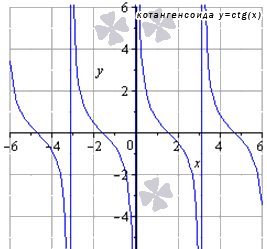
График данной функции называется котангенсоида.

Свойства функции котангенс:

Обратные тригонометрические функции, их свойства и графики

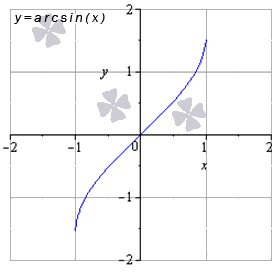
Обратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс. Зачастую, в связи с наличием приставки «арк» в названии, обратные тригонометрические функции называют аркфункциями.

Свойства функции арксинус:

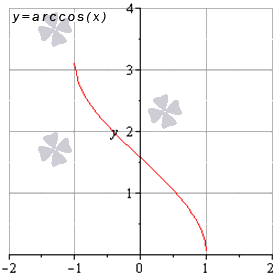
Свойства функции арккосинус:

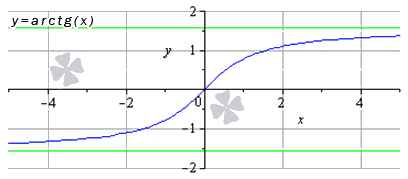
Свойства функции арктангенс:

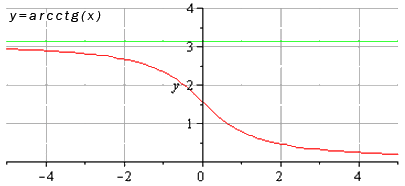
Свойства функции арккотангенс:

Источник

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.

теория по математике 📈 функции

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Таким образом, мы нашли нуль функции: х=2

Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Источник

Что такое Функция?

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник