что такое порядок величины
Порядок расчета величин
Физика > Порядок расчета величин
Порядок величин – класс масштаба любой суммы, в которой каждый класс обладает значением фиксированного отношения к предыдущему классу.
Задача обучения
Основные пункты
Термин
Порядок величин – класс масштаба или величина любой суммы, где каждый следующий класс будет вмещать значение фиксированного отношения (10) к предшествующему. То есть, если что-то больше на 2 порядка, то это 100, на 3 – 1000, если превышает на 6 порядков, то в миллион раз больше.
Порядок величины
Порядок величины – класс масштаба любой суммы, в которой каждый класс вмещает значение стабильного отношения к показателю, которые следовал ранее. Так как это широко используемая система, то за величину масштабирования берут 10. Подобные различия в порядке величины можно вычислить по логарифмической шкале в десятках раз. Ученые часто оперируют подобными понятиями и, если точный параметр не известен, они пользуются диапазоном порядка конкретной величины.
Порядок величины чаще всего применяют для приблизительных сравнений и отражают серьезные отличия. Если два числа разнятся одним порядком, то значит одно в 10 раз больше второго. Если установлено отличие в 2 порядка, тогда в 100 раз. Если два числа одного порядка делят еще и один масштаб, то большее значение меньше десятикратного второго.
Если в науке важно добиваться точности, то в случае с порядком величин часто достаточно, чтобы оценка пребывала в приблизительном значении. Конечно, для опытных исследователей все эти понятия кажутся элементарными, но для неподготовленного читателя они могут быть наравне с египетскими иероглифами.
Пример оценки
Давайте проведем оценку порядка величины. Решим задачку: какой процент от цены помидора исходит из стоимости погрузки его в грузовик.
Начнем с неправильных действий. Итак, водитель должен за поездку сколотить себе прибыль. Не будем вычеркивать из расчета стоимость бензина, обслуживание транспорта и т.д. Получим, например, 2000. В грузовике находится 5000 помидоров, поэтому стоимость одного – 40 центов. Получается, что стоимость помидора приравнивается к транспортировке одной штуки.
Главная загвоздка в том, что наш разум не привык точно оценивать площадь или объем. На намного проще пользоваться линейной оценкой и рассчитывать объем уже оттуда.
Сколько конфет в банке? Если гадать напрямую, то наверняка ошибетесь. Лучше всего рассчитать линейные размеры, а потом вывести объем
Порядок расчета величин
Физика > Порядок расчета величин
Порядок величин – класс масштаба любой суммы, в которой каждый класс обладает значением фиксированного отношения к предыдущему классу.
Задача обучения
Основные пункты
Термин
Порядок величин – класс масштаба или величина любой суммы, где каждый следующий класс будет вмещать значение фиксированного отношения (10) к предшествующему. То есть, если что-то больше на 2 порядка, то это 100, на 3 – 1000, если превышает на 6 порядков, то в миллион раз больше.
Порядок величины
Порядок величины – класс масштаба любой суммы, в которой каждый класс вмещает значение стабильного отношения к показателю, которые следовал ранее. Так как это широко используемая система, то за величину масштабирования берут 10. Подобные различия в порядке величины можно вычислить по логарифмической шкале в десятках раз. Ученые часто оперируют подобными понятиями и, если точный параметр не известен, они пользуются диапазоном порядка конкретной величины.
Порядок величины чаще всего применяют для приблизительных сравнений и отражают серьезные отличия. Если два числа разнятся одним порядком, то значит одно в 10 раз больше второго. Если установлено отличие в 2 порядка, тогда в 100 раз. Если два числа одного порядка делят еще и один масштаб, то большее значение меньше десятикратного второго.
Если в науке важно добиваться точности, то в случае с порядком величин часто достаточно, чтобы оценка пребывала в приблизительном значении. Конечно, для опытных исследователей все эти понятия кажутся элементарными, но для неподготовленного читателя они могут быть наравне с египетскими иероглифами.
Пример оценки
Давайте проведем оценку порядка величины. Решим задачку: какой процент от цены помидора исходит из стоимости погрузки его в грузовик.
Начнем с неправильных действий. Итак, водитель должен за поездку сколотить себе прибыль. Не будем вычеркивать из расчета стоимость бензина, обслуживание транспорта и т.д. Получим, например, 2000. В грузовике находится 5000 помидоров, поэтому стоимость одного – 40 центов. Получается, что стоимость помидора приравнивается к транспортировке одной штуки.
Главная загвоздка в том, что наш разум не привык точно оценивать площадь или объем. На намного проще пользоваться линейной оценкой и рассчитывать объем уже оттуда.
Сколько конфет в банке? Если гадать напрямую, то наверняка ошибетесь. Лучше всего рассчитать линейные размеры, а потом вывести объем
An порядок величины является приближением логарифм значения относительно некоторого контекстуально понимаемого эталонного значения, обычно десяти, интерпретируемого как основание логарифма и представителя значений величины один. Логарифмические распределения являются обычными по своей природе, и рассмотрение порядка величины значений, взятых из такого распределения, может быть более интуитивным. Когда опорное значение равно десять, порядок может быть понят как количество цифр в представлении базы-10 значения. Аналогичным образом, если опорное значение является одним из определенных степеней числа двух, величина может быть понята как объем памяти компьютера необходимо хранить точное целое значение.
Отличия по порядку величины может быть измеренный на базе-10 логарифмическая шкала в «десятилетия”(То есть, множитель десять). [1] Примеры чисел разной величины можно найти на Порядки величины (числа).
Содержание
Определение
Использует
Порядки величин используются для приблизительного сравнения. Если числа различаются на порядок, Икс является о в десять раз отличается по количеству, чем у. Если значения различаются на два порядка, они различаются примерно в 100 раз. Два числа одного порядка имеют примерно одинаковый масштаб: большее значение в десять раз меньше меньшего.
| Прописью (длинная шкала) | Прописью (короткая шкала) | Префикс (символ) | Десятичный | Мощность довольно часто | Порядок величина |
|---|---|---|---|---|---|
| квадриллионный | септиллионный | йокто- (у) | 0.000 000 000 000 000 000 000 001 | 10 −24 | −24 |
| триллиард | секстиллионный | зепто- (z) | 0.000 000 000 000 000 000 001 | 10 −21 | −21 |
| триллионный | квинтиллионный | атто- (а) | 0.000 000 000 000 000 001 | 10 −18 | −18 |
| биллиардный | квадриллионный | фемто- (ф) | 0.000 000 000 000 001 | 10 −15 | −15 |
| миллиардный | триллионный | пико- (п) | 0.000 000 000 001 | 10 −12 | −12 |
| миллиардная | миллиардный | нано- (п) | 0.000 000 001 | 10 −9 | −9 |
| миллионный | миллионный | микро- (µ) (строчные Му символ) | 0.000 001 | 10 −6 | −6 |
| тысячный | тысячный | милли- (м) | 0.001 | 10 −3 | −3 |
| сотый | сотый | санти- (с) | 0.01 | 10 −2 | −2 |
| десятый | десятый | деци- (d) | 0.1 | 10 −1 | −1 |
| один | один | 1 | 10 0 | 0 | |
| десять | десять | дека- (да) U + 3372 (㍲) | 10 | 10 1 | 1 |
| сотня | сотня | гекто- (ч) | 100 | 10 2 | 2 |
| тысяча | тысяча | кило- (к) | 1000 | 10 3 | 3 |
| миллион | миллион | мега- (М) | 1 000 000 | 10 6 | 6 |
| миллиард | миллиард | гига- (G) | 1 000 000 000 | 10 9 | 9 |
| миллиард | триллион | тера- (Т) | 1 000 000 000 000 | 10 12 | 12 |
| бильярд | квадриллион | пета- (P) | 1 000 000 000 000 000 | 10 15 | 15 |
| триллион | квинтиллион | exa- (E) | 1 000 000 000 000 000 000 | 10 18 | 18 |
| триллиард | секстиллион | зетта- (Z) | 1 000 000 000 000 000 000 000 | 10 21 | 21 |
| квадриллион | септиллион | yotta- (Y) | 1 000 000 000 000 000 000 000 000 | 10 24 | 24 |
| Прописью (длинная шкала) | Прописью (короткая шкала) | Префикс (символ) | Десятичный | Мощность довольно часто | Порядок величина |
Расчет по порядку величины
Оценка по порядку величины
Порядок разницы
Разница по порядку величины между двумя значениями составляет 10 раз. Например, масса планеты Сатурн в 95 раз больше, чем земной шар, так что Сатурн два порядка массивнее Земли. Различия по порядку величины называются десятилетия при измерении на логарифмическая шкала.
Недесятичные порядки величины
Другие порядки величины можно рассчитать, используя базы кроме 10. Древние греки ранжировали ночную яркость небесных тел по 6 уровням, в которых каждый уровень был корнем пятой степени из ста (около 2,512) яркости ближайшего более слабого уровень яркости, и, таким образом, самый яркий уровень, который на 5 порядков ярче самого слабого, указывает на то, что это (100 1/5 ) 5 или фактор в 100 раз ярче.
| Порядок величины | Является бревно10 из | Журнал 1 000 000 из | Короткая шкала | Длинная шкала |
|---|---|---|---|---|
| 1 | 10 | 1 000 000 | миллион | миллион |
| 2 | 100 | 1 000 000 000 000 | триллион | миллиард |
| 3 | 1000 | 1 000 000 000 000 000 000 | квинтиллион | триллион |
SI единицы в таблице справа используются вместе с Префиксы SI, которые были разработаны с учетом в основном базовой 1000 звездной величины. Стандартные префиксы МЭК с базой 1024 были изобретены для использования в электронной технике.
Древний видимые величины для яркости звезд используется база 100 5 ≈ 2.512 
и наоборот. Однако модернизированная версия превратилась в логарифмическую шкалу с нецелыми значениями.
Чрезвычайно большие числа
Для чрезвычайно большие числа, обобщенный порядок величины может быть основан на их двойной логарифм или же суперлогарифм. Округление их в меньшую сторону до целого числа дает категории между очень «круглыми числами», округление их до ближайшего целого числа и применение обратной функции дает «ближайшее» круглое число.
Двойной логарифм дает категории:
(первые два упомянутых и расширение слева могут быть не очень полезными, они просто демонстрируют, как последовательность математически продолжается влево).
Суперлогарифм дает категории:
«Средние точки», определяющие, какое из круглых чисел ближе, в первом случае:
и, в зависимости от метода интерполяции, во втором случае
Для чрезвычайно малых чисел (в смысле близких к нулю) ни один метод не подходит напрямую, но обобщенный порядок величины взаимный можно считать.
Подобно логарифмическая шкала можно иметь двойную логарифмическую шкалу (пример предоставлен здесь) и суперлогарифмической шкале. Все интервалы имеют одинаковую длину, а «середины» фактически находятся на полпути. В более общем смысле точка на полпути между двумя точками соответствует обобщенный ж-иметь в виду с ж(Икс) соответствующая функция log log Икс или утомительный Икс. В случае журнала регистрации Икс, это среднее значение двух чисел (например, 2 и 16 дает 4) не зависит от основания логарифма, как и в случае log Икс (среднее геометрическое, 2 и 8 дают 4), но в отличие от журнала журнала журнала Икс (4 и 65 536 дает 16, если основание равно 2, но не иначе).
Значение словосочетания «порядок величины»
, выражающих некоторые количества, в рамках которого все величины имеют фиксированное отношение
к соответствующим величинам предыдущего класса.
Чаще под порядком подразумевают не сам класс эквивалентности
а некоторую его числовую характеристику, задающую этот класс при данных условиях (например, порядковый номер класса
при условии, что некоторый класс
был задан или подразумевается).
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова неоколониализм (существительное):
Ассоциации к слову «порядок»
Ассоциации к слову «величина»
Синонимы к словосочетанию «порядок величины»
Предложения со словосочетанием «порядок величины»
Цитаты из русской классики со словосочетанием «порядок величины»
Сочетаемость слова «порядок»
Сочетаемость слова «величина»
Понятия со словосочетанием «порядок величины»
Площади различных порядков могут быть сопоставлены для визуального представления их относительности. Данные, приведённые ниже, должны рассматриваться как «типичные величины», расчётные величины округлены.
Афоризмы русских писателей со словом «порядок»
Отправить комментарий
Дополнительно
Предложения со словосочетанием «порядок величины»
Хотя я уже успел убедиться в его расплывчатости и неточности, порядок величин непременно должен сохраняться.
Возможно, между сторонами существуют разногласия относительно конкретных сумм, но согласно показаниям обеих сторон, очевидно, порядок величин был именно таким.
Но в нашей обычной жизни это явление не особенно важно, поскольку скорость нашего движения относительно любого другого наблюдателя никогда по порядку величины не приближается к скорости света.
Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок. Зачем это придумали.
Стандартная, она же научная форма записи числа. Порядок величины. Разница на порядок. Зачем это придумали.
Любое рациональное число может быть представлено в виде:
 |  |
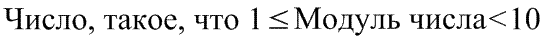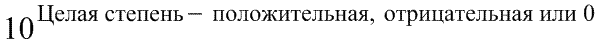| Эта часть записи называется Мантиссой числа в стандартной (научной) форме. | А эта часть называется Порядком числа в стандартной (научной) форме. |
Пример 2 : Величины 890 и 45932, записанные в стандартной форме выглядят как: 8,9*10 2 и 4,5932*10 4 и отличаются на 2 порядка = имеют разницу в 2 порядка. Числа 7,5 и 75 различаются на порядок ( на 1 порядок) = имеют разницу в 1 порядок, что бы там в телевизоре не думали. И так далее.
Очевидно, что при сложении и вычитании чисел записанных в стандартной форме и имеющих один порядок, достаточно сложить или вычесть мантиссы.
Пример 3: 7,2*10 34 + 1,2*10 34 = (7,2+ 1,2)*10 34 =8,4*10 34
Пример 4: 9,9*10 13 + 9,9*10 12 =9,9*10 13 + 0,99*10 13 = (9,9+ 0,99)*10 13 =10,89*10 13 =1,089*10 14
Очень удобно проводить операции умножения и деления с числами, записанными в стандартной форме, пользуясь правилами действий со степенями:
Пример 5: 4,0*10 3 x 2,25*10 2 =(4,0×2,25)x(10 3+2 )= 9,0*10 5
Пример 6: 5,0*10 6 /2,5*10 3 =(5,0/2,5)x(10 6-3 )= 2,0*10 3