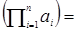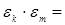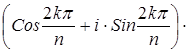что такое порядок циклической группы

20.12.202325.09.2023 admin 0 Comments

Циклические подгруппы

Конечные группы

Группа (полугруппа) называется конечной, если она состоит из конечного числа элементов. Число элементов конечной группы называется её порядком. Любая подгруппа конечной группы конечна. И если НÍG – подгруппа группы G, то для любого элемента аÎG множество Н_а=<х: x=h◦a, для любых hÎH> называется левым классом смежности для G относительно Н. Понятно, что число элементов в Н_а равно порядку Н. (Аналогично можно сформулировать определение _аН – правого класса смежности относительно Н).

Важно то, что для любой подгруппы Н группы G любые два левых (правых) класса смежности по Н либо совпадают, либо не пересекаются, поэтому любая группа может быть представлена как объединение непересекающихся левых (правых) классов смежности по Н.

Такое разбиение группы на левые (правые) классы смежности называется разложением группы по подгруппе Н.

Теорема 2.6.1. Порядок конечной группы делится на порядок любой её подгруппы.

Доказательство. Так как G – конечная группа, то и любая её подгруппа Н имеет конечный порядок. Рассмотрим разложение группы по подгруппе Н. В каждом классе смежности в этом разложении число элементов одинаково и равно порядку Н. Поэтому, если n – порядок группы G, а k – порядок подгруппы Н, то n=m×k, где m – число классов смежности по Н в разложении группы G.

Если для любого элемента aÎG Þ Н_a = _аН (левый и правый классы смежности по подгруппе Н совпадают), то Н называется нормальным делителем группы G.

Утверждение: если G – коммутативная группа, то любая её подгруппа Н является нормальным делителем G.

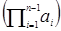
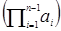
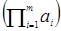
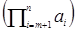
Ввиду ассоциативности действия в группе (полугруппе) можно говорить о «произведении» трех элементов (а◦b◦c) =(а◦b)◦c = а◦(b◦c). Аналогично вводится понятие сложного произведения из n элементов: а₁◦а₂◦…◦а_n = ◦ а_n = = ◦.

В аддитивной группе аналогом степени элемента a n будет n‑кратное к нему, обозначаемое обычно na, которое не стоит воспринимать как произведение n на а, поскольку nÎℕ и, возможно, nÏG. Т.о. na⇋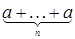, где nÎℕ, и 0а=е⇋0, и (‑n)a = ‑(na) = n(‑a) для любого натурального n, где (‑a) – обратный к aÎG.

Легко показать, что при выбранных обозначениях для любых целых чисел m и n и для любого aÎG выполняются известные свойства: а) при мультипликативной записи a n ◦a m = a n + m и (a n ) m = a nm ; б) при аддитивной записи na+ma = (n+m)a и n(ma)=(nm)a.

Подгруппа А_g называется циклической подгруппой группы G, порожденной элементом g. Эта подгруппа всегда коммутативна, даже если сама G не коммутативна. Если группа G совпадает с одной из своих циклических подгрупп, то она называется циклической группой, порожденной элементом g.

Если все степени элемента g различны, то группа G называется бесконечной циклической группой, а элемент g – элементом бесконечного порядка.

Если среди элементов циклической группы имеются равные, например, g k =g m при k>m, то g k ‑ m =e; и, обозначив k-m через n, получим g n =e, nÎℕ.

Наименьший натуральный показатель n такой, что g n =e, называется порядком элемента g, а сам элемент g называется элементом конечного порядка.

Такой элемент всегда найдется в конечной группе, но может быть и в бесконечной группе.

Группы, все элементы которых имеют конечный порядок, называются периодическими.

1) Всякая группа обладает единственным элементом первого порядка <e>, порождающим циклическую подгруппу первого порядка, состоящую из одного элемента е.

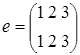
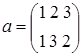
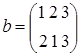
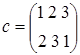
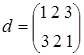
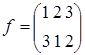
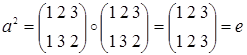
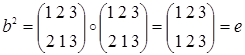
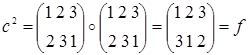
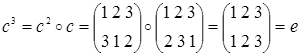
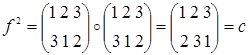
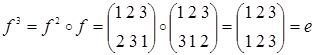
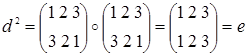
2) Рассмотрим группу подстановок S₃, состоящую из элементов: , , , , , . Порядок S₃=6. Порядок элемента а равен 2, т.к. . Порядок элемента b также равен 2, т.к. . Порядок элемента с равен 3, т.к. и . Порядок элемента f также равен 3, т.к. и . И, наконец, порядок d равен 2, т.к. . Тем самым, циклические подгруппы S₃, порожденные элементами e, a, b, d, c и f, соответственно равны: <e>, <e, a>, <e, b>, <e, d>, <e, c, f> и <e, f, c>, где последние две совпадают. Заметим также, что порядок каждой циклической подгруппы делит порядок группы без остатка. Справедлива следующая теорема.

Теорема 2.7.1. (Лагранжа) Порядок конечной группы делится на порядок любого её элемента (т.к. порядок элемента и порядок циклической подгруппы, порожденной им, совпадают).

Отсюда также следует, что любой элемент конечной группы при возведении в степень порядка группы дает единицу группы. (Т.к. g m =g nk =e k =e, где m – порядок группы, n – порядок элемента g, k – целое число).

В группе S₃ подгруппа Н=<e, c, f> является нормальным делителем, а подгруппы 2‑го порядка нормальными делителями не являются. Это легко проверить, найдя левый и правый классы смежности по Н для каждого элемента группы. Например, для элемента а левый класс смежности Н_а=<е ◦ а, с ◦ а, f ◦ a> = <а, b, d> и правый класс смежности _аН=<а ◦ е, а ◦ c, а ◦ f> = <а, d, b> совпадают. Аналогично для всех остальных элементов S₃.

3) Множество всех целых чисел со сложением образует бесконечную циклическую группу с порождающим элементом 1 (или –1), т.к. любое целое число кратно 1.

4) Рассмотрим множество корней n‑ой степени из единицы: Е_n=. Это множество является группой относительно операции умножения корней. Действительно, произведение любых двух элементов e_k и e_m из E_n, где k, m £ n‑1, также будет элементом E_n, поскольку = = , где r=(k+m) mod n и r £ n‑1; умножение ассоциативно, нейтральный элемент е=e₀=1 и для любого элемента e_k имеется обратный и . Эта группа циклическая, её порождающим элементом является первообразный корень . Нетрудно видеть, что различными являются все степени: , далее для k³n корни начинают повторяться. На комплексной плоскости корни расположены на окружности единичного радиуса и делят её на n равных дуг, как показано на рисунке 11.

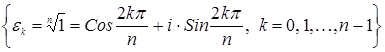
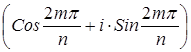
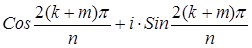
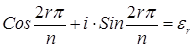
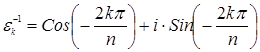
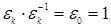
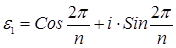
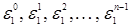
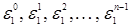
Последними двумя примерами исчерпываются по существу все циклические группы. Поскольку справедлива следующая теорема.

Теорема 2.7.2. Все бесконечные циклические группы изоморфны между собой. Все конечные циклические группы порядка n изоморфны между собой.

Пусть теперь (G, ∘ ) – конечная циклическая группа порядка n с порождающим элементом g. Тогда каждому элементу g k ÎG единственным способом можно сопоставить элемент e_kÎE_n (0£k k )=e_k. И при этом для любых g k и g m ÎG следует, что f(g k ∘ g m )= f(g k ) ∘ f(g m ), поскольку f(g k ∘ g m )= f(g k + m )= f(g r ), где r=(k+m) mod n, и f(g r )=e_r=e_k×e_m. Понятно, что такое сопоставление является биективным отображением.

Источник

Что такое порядок циклической группы

Покажем, что всякая подгруппа циклической группы тоже циклическая.

ТЕОРЕМА 3.7. Любая подгруппа циклической группы есть циклическая группа.

Доказательство. Пусть — мультипликативная циклическая группа с образующим элементом а. Пусть — подгруппа группы 5. Теорема, очевидно, верна, если Я содержит только один элемент. Предположим, что Я содержит более одного элемента, Подгруппа содержит хотя бы одну положительную степень элемента а, ибо если то . Пусть — элемент из Я с наименьшим положительным показателем степени s. Всякий элемент из Я есть элемент вида . Если , то s делит k. В самом деле, по теореме о делении с остатком (теорема 4.4.4), для чисел k и s существуют такие целые числа q и , что

Ввиду . Так как то в силу выбора числа s значит, . Таким образом, множество состоит из степеней элемента . Следовательно, является циклической группой с образующим элементом