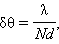что такое порядок спектра
Учебники
Журнал «Квант»
Общие
Дифракционная решетка. Дифракционный спектр
Важную роль в прикладной оптике играют явления дифракции на отверстиях в форме щели с параллельными краями. При этом использование дифракции света на одной щели в практических целях затруднено из-за слабой видимости дифракционной картины. Широко используются дифракционные решетки.
Дифракционная решетка — спектральный прибор, служащий для разложения света в спектр и измерения длины волны. Различают прозрачные и отражающие решетки. Дифракционная решетка представляет собой совокупность большого числа параллельных штрихов одинаковой формы, нанесенных на плоскую или вогнутую полированную поверхность на одинаковом расстоянии друг от друга.
В прозрачной плоской дифракционной решетке (рис. 17.22) ширина прозрачного штриха равна а, ширина непрозрачного промежутка — Ь. Величина \(d = a + b = \frac<1>
Пусть плоская монохроматическая волна падает нормально к плоскости решетки (рис. 17.22). По принципу Гюйгенса—Френеля каждая щель является источником вторичных волн, способных интерферировать друг с другом. Получившуюся дифракционную картину можно наблюдать в фокальной плоскости линзы, на которую падает дифрагированный пучок.
Допустим, что свет дифрагирует на щелях под углом \(\varphi.\) Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, для данного направления \(\varphi\) будут одинаковыми в пределах всей дифракционной решетки:
В тех направлениях, для которых разность хода равна четному числу полуволн, наблюдается интерференционный максимум. Наоборот, для тех направлений, где разность хода равна нечетному числу полуволн, наблюдается интерференционный минимум. Таким образом, в направлениях, для которых углы \(\varphi\) удовлетворяют условию
\(d \sin \varphi = m \lambda (m = 0,1,2, \ldots),\)
При наблюдении дифракции в немонохроматическом (белом) свете все главные максимумы, кроме нулевого центрального максимума, окрашены. Это объясняется тем, что, как видно из формулы \(\sin \varphi = \frac
Ширина спектра зависит от постоянной решетки и увеличивается при уменьшении d. Максимальный порядок спектра определяется из условия \(
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 517-518.
В компьютерном варианте работы отсчет показаний производится автоматически.
5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Целью работы является изучение дифракционной решетки, нахождение ее характеристик и определение с ее помощью длины световой волны.
ЗАДАЧА 1. ОПРЕДЕЛЕНИЕ ДЛИН ВОЛН СПЕКТРАЛЬНЫХ ЛИНИЙ.
Прежде чем включить источник исследуемого излучения, рекомендуется произвести пробный отсчет по шкалам спектрогониометра. Затем включают ртутную лампу и устанавливают ее напротив входной щели коллиматора. Дифракционная решетка ставится перпендикулярно к направлению пучка света.
Далее поворачивают алидаду грубо от руки (винт 12 разжат) до тех пор, пока визирная линия зрительной трубы не будет наведена на нулевой, центральный максимум. Пользуясь микрометрическим винтом 2 и маховичками 7 и 8, получают четкое и узкое изображение коллиматорной щели. Поворачивая алидаду от руки (винт 12 разжат) влево и вправо от нулевого максимума, просматривают весь спектр и находят нужные спектральные линии в спектре первого порядка. После этого приступают к измерениям.

Следует учесть, что после наведения визира на каждую очередную линию требуется дополнительная фокусировка этой линии маховичками 7 и 8.
Измерения проводятся для линий спектра первого порядка.
Результаты измерений заносятся в табл. II.I (см. приложение). Значение длины волны l получают, используя формулу (3.2):

Постоянная d решетки задается в прилагаемой к установке табличке.
ЗАДАЧА 2. ОПРЕДЕЛЕНИЕ НАИВЫСШЕГО ПОРЯДКА ДИФРАКЦИОННЫХ
СПЕКТРОВ, РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ И УГЛОВОЙ ДИСПЕРСИИ
Максимальное значение порядка m max дифракционных спектров может быть определено из условия (3.2) главных максимумов, записанного для нормального падения света на решетку:

Разрешающая способность R дифракционной решетки характеризует ее способность разделять (разрешать) спектральные линии, мало отличающиеся по длинам волн. По определению

Из этих уравнений следует, что
и разрешающая способность решетки оказывается равной
Таким образом, разрешающая способность решетки зависит от порядка m спектра и от общего числа N штрихов рабочей части решетки, т.е. той части, через которую проходит исследуемое излучение и от которой зависит результирующая дифракционная картина.
Угловая дисперсия D дифракционной решетки характеризует угловое расстояние между близкими спектральными линиями. По определению


Разрешающая способность R находится для спектра первого порядка ( m = 1) по формуле 5.4. Число рабочих щелей задается в прилагаемой к установке таблице.
В конце работы необходимо сделать выводы.
Укажите тип решетки, используемой в лабораторной работе (отражательная, прозрачная), число штрихов на 1 мм ( N/L ) и наибольший прядок m max спектра.
Оцените, какую наименьшую разность D l может разрешить данная дифракционная решетка в выбранной Вами области спектра.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ
1. В чем состоит явление дифракции света?
2. Сформулируйте принцип Гюйгенса-Френеля.
3. Что такое разрешающая способность R дифракционной решетки и от чего она зависит?
4. Как экспериментально определить угловую дисперсию D дифракционной решетки?
5. Какой вид имеет дифракционная картина, полученная от прозрачной решетки?
6. Какой цвет обеспечивает наилучшую разрешающую способность дифракционной решетки?
7. Сколько штрихов должна иметь дифракционная решетка длиной L = 1 см, если спектр второго порядка отсутствует в видимой области? (Длины волн видимого спектра т 390 до 78 8 нм).
8. Чем различаются интерференционные картины от двух щелей на расстоянии 1 мкм и дифракционной решетки с постоянной d = 1 мкм?
1. Савельев И.В. Курс общей физики. Т.2. М.: Наука, 1979. С. 398-406.
2. Ландсберг Г.С. Оптика. М.: Наука, 1976. С. 198-205, 211-215.
3. Физический практикум / Под ред. В.И.Ивероновой. М.: Наука, 1968.
4. Иродов И.Е. Физический практикум. М.: МИФИ, 1967.
Что такое порядок спектра
Первый опыт по разложению белого света в спектр был осуществлен И. Ньютоном (1672 г.).
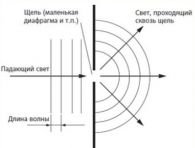
Простейшая дифракционная решетка состоит из прозрачных участков (щелей), разделенных непрозрачными промежутками. На решетку с помощью коллиматора направляется параллельный пучок исследуемого света. Наблюдение ведется в фокальной плоскости линзы, установленной за решеткой (рис. 3.10.3).
В каждой точке на экране в фокальной плоскости линзы соберутся лучи, которые до линзы были параллельны между собой и распространялись под определенным углом к направлению падающей волны. Колебание в точке является результатом интерференции вторичных волн, приходящих в эту точку от разных щелей. Для того, чтобы в точке наблюдался интерференционный максимум, разность хода между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн:
Следует обратить внимание на то, что в каждой точке фокальной плоскости линзы происходит интерференция волн, приходящих в эту точку от щелей решетки. Это так называемая многоволновая (или «многолучевая») интерференция. Распределение световой энергии в плоскости наблюдения резко отличается от того, которое получается в обычных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, потому амплитуда колебаний возрастает в раз, а интенсивность в раз по сравнению с колебанием, которое возбуждает волна только от одной щели.
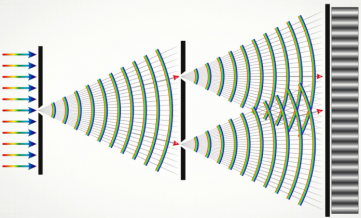
Здесь для простоты полагается, что дифракционные углы достаточно малы. Следовательно,
|
где – полный размер решетки. Это соотношение находится в полном согласии с теорией дифракции в параллельных лучах, согласно которой дифракционная расходимость параллельного пучка лучей равна отношению длины волны к поперечному размеру препятствия.
Можно сделать важный вывод: при дифракции света на решетке главные максимумы чрезвычайно узки. Рис. 3.10.5 дает представление о том, как меняется острота главных максимумов при увеличении числа щелей решетки.
Дифракция света
теория по физике 🧲 оптика
Дифракция — явление, присущее всем волновым процессам подобно интерференции. Чтобы лучше понять, в чем заключается явление дифракции света, сначала рассмотрим дифракцию механических волн.
Дифракция механических волн
Иногда на пути волны встречаются препятствия разных размеров. Если препятствия небольшие, волны легко их огибают и смыкаются за ними. Поэтому морские волны свободно огибают выглядывающие из воды камни и распространяются за ними так, как если бы их не было совсем. Если размер препятствия больше длины волны, за ним образуется «тень» — область, в которую волны проникнуть не могут.
На рисунке ниже видно, что за мелкими камнями волны распространяются так же, как если бы их не было. Но за большой глыбой поверхность воды спокойная — волны в эту область не проникают.
Внимание! Малыми препятствиями будем считать те, размеры которых намного меньше длины распространяющейся волны или сравнимы с ней.
Способность волн огибать препятствия является следствием отклонения распространения волн от их прямолинейного распространения. Такой способностью обладают не только волны на поверхности воды, но и звуковые волны. Вы услышите, как сигналит автомобиль за домом, который стоит между ним и вами препятствием именно благодаря дифракции. Звуковая волна обогнет дом и продолжит распространяться за ним. По этой же причине в лесу так далеко распространяется клик «Ау!» — деревья для звуковой волны не являются серьезным препятствием, и она их легко огибает.
Дифракция — явление отклонения от прямолинейного распространения волн.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней. Это явление встречается в природе, но его также можно вызвать искусственно. К примеру, дифракцию волн на поверхности воды можно наблюдать, налив воду в ванночку и поставив на пути возбуждаемых волн искусственное препятствие.
Если на пути распространения волн поставить экран с узкой щелью, размеры которой меньше длины волны, то увидим, что за ней начинает распространяться круговая волна. Такая же волна получилась, если бы в щели экрана находилось колеблющееся тело — источник волн.
Если же на пути распространения волны поставить экран с широкой щелью, за ним будет распространяться волна почти такой же формы. Волновая поверхность в этом случае искривляется только по краям щели.
Понять, почему появляется явление дифракции волн, помогает принцип Гюйгенса. Согласно ему, каждая точка волновой поверхности является источником вторичных волн. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.
Дифракция световых волн
Если свет — это волна, то ему тоже должно быть присуще явление дифракции. Однако наблюдать дифракцию света сложно. Ведь дифракцию можно наблюдать тогда, когда препятствие сравнимо с длиной волны или меньше ее. А длина световой волны очень мала. Поэтому чтобы наблюдать дифракцию света, нужны очень малые препятствия.
Дифракция света на узкой щели
Наблюдать отклонение от прямолинейного распространения света можно, если пропустить пучок световых волн через узкую щель. При этом светлое пятно на экране будет больше, чем сама щель. Это возможно только в случае, если свет отклоняется от своего прямолинейного распространения.
Опыт Юнга
В 1802 г. Т. Юнг, который открыл интерференцию света, поставил классический опыт по наблюдению дифракции. В непрозрачной ширме он проколол булавкой два небольших отверстия В и С на малом расстоянии друг от друга. Эти отверстия он осветил узким световым пучком, прошедшим через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, определила успех эксперимента. Интерферируют ведь только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А вызвала в отверстиях В и С образование когерентных источников световых волн. Вследствие дифракции от отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции этих двух световых волн на экране появлялись картина, состоящая из чередующихся светлых и темных полос.
Закрыв одно из отверстий, Юнг обнаружил, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые ученый измерил длины волн, соответствующие световым лучам разного цвета. И ему удалось сделать это с высокой точностью.
Принцип Гюйгенса — Френеля
Исследование дифракции завершил французский ученый О. Френель. Он занимался детальным исследованием различных случаев дифракции, что позволило ему разработать количественную теорию дифракции. Она помогла физику получить точные расчеты дифракционной картины, которая возникала при огибании светом различных препятствий. Френелю также удалось впервые объяснить, почему в однородной среде свет распространяется прямолинейно.
Успех Френеля объясняется тем, что он стал первым, кто решил объединить принцип Гюйгенса с идеей интерференции вторичных волн. В результате зародилась теория, которая получила название принципа Гюйгенса — Френеля:
Волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.
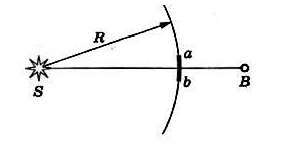
Чтобы вычислить амплитуду световой волны в любой точке пространства, необходимо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду колебаний в рассматриваемой точке пространства. Такие расчеты дали объяснение тому, как свет от точечного источника S, являющегося источником сферических волн, достигает любой точки В пространства.
Если рассмотреть вторичные источники на сферической волновой поверхности радиусом R, то результат сложения вторичных волн от этих источников в точке В оказывается таким, как если бы только вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, распространяющие от источников, расположенных на остальной части поверхности, гасят друг друга в результате сложения. Поэтому все происходит так, как если бы свет распространялся вдоль прямой SB, т. е. прямолинейно. Эта теория Френеля доказала закон прямолинейного распространения света в однородной среде и позволила рассмотреть дифракцию с количественной точки зрения.
Внимание! Закон прямолинейного распространения света и другие законы геометрической оптики выполняются достаточно точно лишь в том случае, если размеры препятствий на пути распространения света много больше длины световой волны.
Дифракционные картины от различных препятствий
Расчеты Френеля получили экспериментальное подтверждение. Из-за малой длины световой волны угол ее отклонения от прямолинейного направления распространения небольшой. Поэтому наблюдать дифракцию можно только при использовании очень маленьких препятствий. Другой вариант наблюдения этого явления — расположение экрана вдали от препятствия.
Так, чтобы наблюдать дифракцию при расстоянии между экраном и препятствием в 1 м, размеры этого препятствия должны составлять сотые доли миллиметра. Если расстояние от препятствия до экрана увеличить до нескольких сотен метров, то размеры препятствия могут быть несколько сантиметров. Если расстояние между экраном и препятствием будет составлять несколько километров, дифракцию можно будет наблюдать при размерах препятствия в несколько метров.
Дифракционная картина — картина на экране, полученная в результате интерференции вторичных световых волн.
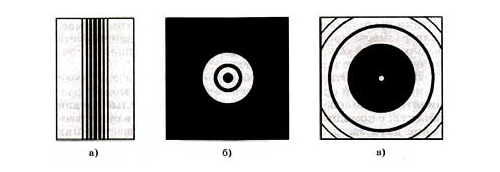
Подобную картину вы уже видели на картинке, иллюстрирующей опыт Юнга. Так, дифракционная картина от двух малых щелей — это чередующиеся темные и светлые полосы. Если использовать другие препятствия, картина будет меняться. На рисунке ниже схематично показаны дифракционные картины от различных препятствий: а — от тонкой проволочки; б — от круглого отверстия; в — от круглого экрана.
Вместо тени проволочка оставляет на экране светлые и темные полосы. В центре дифракционной картины, полученного от отверстия, появляется темное пятно, окруженное светлыми и темными кольцами. В центре тени, образованной круглым экраном, видно светлое пятнышко, а сама тень окружена темными кольцами. Если изменять диаметр отверстия, в центре дифракционной картины можно получить как светлое, так и темное пятно, окруженное либо темными, либо светлыми кольцами соответственно.
Дифракционная решетка
Дифракционная решетка — оптический прибор, принцип действия которого основан на явлении дифракции.
Дифракционная решетка представляет собой совокупность большого числа очень узких щелей, разделенных непрозрачными промежутками. Ее изготавливают путем нанесения на стекло штрихов. Их число может доходить до нескольких тысяч на 1 мм. Общее их число часто превышает 100 тысяч. Решетку также можно получить из металла, на котором чередуются участки, отражающие и рассеивающие свет.
Период дифракционной решетки равен сумме ширины прозрачных щелей и ширины непрозрачных промежутков:
Внимание! Обычно изготавливают дифракционные решетки с периодом в 10 мкм.
Пусть на дифракционную решетку с периодом d падает плоская монохроматическая волна, длина волны которой составляет λ.
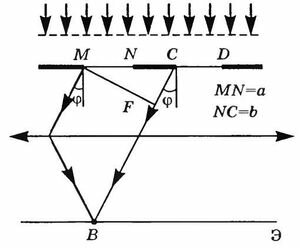
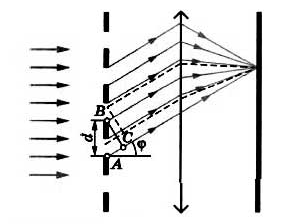
При этом вторичные источники, расположенные в щелях решетки, создают световые волны, распространяющиеся по всем направлениям. Найдем условие, при котором идущие от щелей волны усиливают друг друга (складываются). Для этого рассмотрим волны, распространяющиеся в направлении под углом φ к дифракционной решетке.
Разность хода между волнами от краев соседних щелей равна длине отрезка АС. Если на этом отрезке вмещается целое число длин волн, то волны от всех щелей при сложении будут усиливать друг друга. Из треугольника АВС найдем длину катета АС:
При этом максимумы будут наблюдаться под углом φ в соответствии с условием:
где величина k = 0, 1, 2, … определяет порядок спектра.
Нужно учитывать, что при выполнении условия друг друга усиливают как волны, распространяющиеся от нижних краев щелей, так и волны, распространяющиеся от всех других точек щелей. Каждой точке в первой щели соответствует точка во второй щели, находящаяся на расстоянии d от первой точки. Поэтому разность хода испущенных этими точками вторичных волн равна kλ, и эти волны взаимно усиливаются.
Рассмотрим следующий случай. За решеткой поместим собирающую линзу, а за ней — экран на фокусном расстоянии от линзы. Линза фокусирует лучи, идущие параллельно, в одной точке (в фокусе). В этой точке волны складываются и взаимно усиливаются. Углы φ, удовлетворяющие условию, определяют положение так главных максимумов на экране (соответствующих 1, 2 и т.д. порядку).
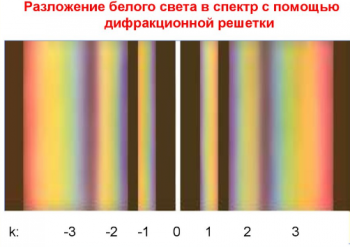
Наряду с картиной, получаемой в результате дифракции света, в случае дифракционной решетки наблюдается дифракционная картина и от отдельных щелей. Интенсивности максимумов в ней меньше интенсивности главных максимумов. Так как положение максимумов (кроме центрального, соответствующего k = 0) зависит от длины волны, то решетка разлагает белый свет в спектр. Чем больше λ, тем дальше от центрального максимума располагается тот или иной максимум, соответствующий данной длине волны.
Каждому значению k соответствует свой порядок спектра. Между максимумами расположены минимумы освещенности. Чем больше число щелей, тем более резко очерчены максимумы и тем более широкими минимумами они разделены.
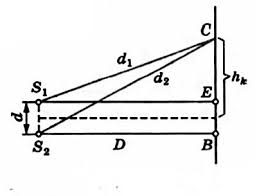
Пример №1. В опыте Юнга по дифракции расстояние между щелями равно d = 7∙10 –4 м. Расстояние от двойной щели до экрана равно D = 2 м. При освещении прибора зеленым светом расстояние между соседними светлыми дифракционными полосами оказалось равным ∆h = 16∙10 –2 м. Вычислите длину волны.
В некоторой точке С экрана будет наблюдаться максимум освещенности при выполнении условия:
где величина k = 0, 1, 2, … — целые числа.
Применим теорему Пифагора к треугольникам S1CE и SsCB:
Вычитая из первого равенства второе, получаем:
d 2 2 − d 2 1 = 2 h k d
( d 2 + d 1 ) ( d 2 − d 1 ) = 2 h k d
Так как расстояние между щелями много меньше расстояния между ними и экраном, то можем считать, что:
Отсюда можем найти расстояние k-той светлой полосы от центра экрана:
Расстояние между соседними полосами равно:
На плоскую непрозрачную пластину с узкими параллельными щелями падает по нормали плоская монохроматическая волна из красной части видимого спектра. За пластиной на параллельном ей экране наблюдается интерференционная картина, содержащая большое число полос. При переходе на монохроматический свет из синей части видимого спектра
а) расстояние между интерференционными полосами увеличится
б) расстояние между интерференционными полосами уменьшится
в) расстояние между интерференционными полосами не изменится
г) интерференционная картина станет невидимой для глаза
Алгоритм решения
Решение
Зависимость расстояния между интерференционными полосами от частоты световых лучей удалось установить экспериментально. Было выяснено, что чем выше частота, тем меньше расстояние между ними. Частота света из синего части спектра больше частоты из красной части спектра. Поэтому при переходе из красной части спектра в синюю часть расстояние между полосами интерференционной картины уменьшится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В прозрачном сосуде, заполненном водой, находится дифракционная решётка. Решётка освещается лучом света лазерной указки, падающим перпендикулярно её поверхности через боковую стенку сосуда. Как изменятся частота световой волны, длина волны, падающей на решётку, и угол между падающим лучом и первым дифракционным максимумом при удалении воды из сосуда?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Когда воды в сосуде не станет, изменится оптическая плотность среды — ею будет воздух, имеющий абсолютный показатель преломления 1 (у воды он равен 1,33).
Частота световой волны — величина постоянная. Она не меняется при изменении любых величин.
Длина световой волны меняется с учетом оптической плотности среды. Она определяется формулой:
В оптически более плотной среде скорость распространения волны уменьшается. Но когда их сосуда была удалена вода, оптическая плотность уменьшилась, значит, скорость волны увеличилась. Так как частота волны — постоянная, а длина волны прямо пропорциональна ее скорости, то при увеличении скорости длина волны тоже увеличится.
В оптически более плотной среде волны отклоняются от прямолинейного распространения сильнее в сторону нормали. Поэтому при удалении воды, когда оптическая среда станет менее плотной, лучи отклонятся от нормали. В этом случае угол между нормалью к решётке и первым дифракционным максимумом увеличится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Дифракционная решётка с периодом 10 –5 м расположена параллельно экрану на расстоянии 0,75 м от него. На решётку по нормали к ней падает пучок света с длиной волны 0,4 мкм. Какого порядка максимум в спектре будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины? Считать sina ≈ tga.