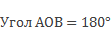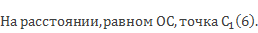что такое положительное направление на координатной прямой
Урок 27 Бесплатно Координаты на прямой
В этом уроке мы познакомимся с положительными и отрицательными числами, поймем, к чему относится нуль.
Не забудем рассказать также про неположительные и неотрицательные числа, а после этого узнаем, что такое координатная прямая и из чего она состоит.
Положительные и отрицательные числа
Начнем с сухих, но емких определений.
Обычно + не пишется, а просто подразумевается.
Мы могли бы их записать и со знаком «+»:
В таком случае нужно читать запись буквально: «плюс два», «плюс одна вторая» и так далее.
Такая запись добавляет громоздкости записи, и обычно все- таки «+» опускают.
Приведем примеры отрицательных чисел:
-3, \(\mathbf<-\frac<1><6>>\), \(\mathbf<-32\frac<4><5>>\), -784285332
Читать в данном случае также нужно дословно: «минус три», «минус одна шестая» и так далее.
Минус уже опустить нельзя, так как тогда получится, что число положительное.
Важные факты:
Если нам надо сравнить два числа, одно из которых положительное, а другое отрицательное, то можно смело утверждать, что число, которое положительно, больше числа, которое отрицательно.
Если надо сравнить число с нулем, то достаточно понять, положительное оно или отрицательное. Если положительное, значит, больше нуля, если же отрицательное, то меньше нуля.
Более подробно про сравнение чисел мы поговорим в следующих уроках, а пока потренируемся отличать положительные и отрицательные числа.
Пройти тест и получить оценку можно после входа или регистрации
Неположительные и неотрицательные числа
Иногда необходимо обозначить множество чисел, больших или равных нулю, или же наоборот, меньших или равных нулю.
Удобно, что для этого есть специальные определения.
Соответственно, если мы хотим привести примеры неотрицательных чисел, то можем привести положительные числа или 0.
Примеры: 0, 1, 956, \(\mathbf<\frac<4><9>>\), \(\mathbf<342\frac<1><9>>\).
В данном случае примерами будут соответственно отрицательные числа или 0.
Если необходимо определить, является ли число неотрицательным или неположительным, то ответить надо следующим образом:
Также отметим важные факты про сравнение неположительных и неотрицательных чисел с нулем:
Пройти тест и получить оценку можно после входа или регистрации
Координатная прямая
Начнем с определения, а потом посмотрим на вариации и примеры координатных прямых в жизни.
Если хотя бы одной из этих трех составляющих нет, то прямая уже не может быть координатной.
Выше мы показали самую простую вариацию координатной прямой.
Но обычно для удобства наносят штрихи по всей длине, чтобы не отмерять единичные отрезки.
Также мы можем подписывать числа не только под точкой начала отсчета и точкой, дающей понимание о длине единичного отрезка, но и под остальными точками тоже.
Если мы не хотим загромождать картинку, то можно отмечать точки с какой-то периодичностью.
Неизменным на всех этих картинках остается наличие трех пунктов из определения:
В жизни координатные прямые, полностью удовлетворяющие нашему определению, могут встречаться довольно редко.
Например, на ртутном термометре подразумевается, что направление совпадает с направлением увеличения чисел на шкале.
На нем же мы видим, что числа стоят не у каждого штриха, а у каждого 5-го или каждого 10-го, так картинка становится более читаемой.
Еще один пример: обычная линейка или рулетка. Тут тоже направление подразумевается, поэтому нельзя однозначно сказать, что это координатная прямая.
На линейке, в отличие от градусника, не часто увидишь отрицательные числа. Действительно, -5 градусов интересуют нас больше, чем -5 сантиметров.
На этом рисунке видно, что у точки начала координат (точка O) координата равна нулю, а у точки (А), дающей информацию о единичном отрезке,
координата- 1.
Чтобы найти координату точки мы должны отсчитать количество единичных отрезков между точкой и точкой начало отсчета. А дальше, если эта точка стоит после точки начала отсчета, то взять количество единичных отрезков. В противном случае, если точка находится перед точкой начала отсчета, то взять количество единичных отрезков со знаком «минус».
Например, чтобы найти координату точки C мы отсчитываем количество отрезков от начала координат; получаем, что их 2, запоминаем это.
Точка С находится справа от точки начала отсчета, или дальше по направлению, чем точка начала отсчета. Значит, берем непосредственно число 2 в качестве координаты.
Между точкой B и точкой начала отсчета 3 единичных отрезка, но если смотреть относительно точки начала отсчета, то она находится левее или раньше по направлению, значит, мы берем количество единичных отрезков со знаком «минус» и координатой точки B будет \(\mathbf<-3>\).
Естественно, единичных отрезков между точкой и точкой начала отрезков может получиться нецелое число.
Точка D идет перед точкой начала отсчета, если смотреть по направлению, а значит, координата должна быть отрицательный.
Таким образом, координата точки D будет равна \(\mathbf<-1.5>\).
Мы не случайно отходим от простых понятий «справа»/«слева», когда говорим о взаимном расположении точек.
Представьте, что направление идет в другую сторону.
Ну и конечно же, прямая может быть вообще расположена вертикально, тогда говорить о направлениях «право»/«лево» вообще не приходится.
Пройти тест и получить оценку можно после входа или регистрации
Что такое положительное направление на координатной прямой
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы узнаете, что такое координатная прямая, научитесь на ней обозначать положительные и отрицательные числа, определять координаты симметричных точек.
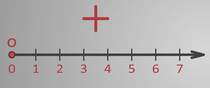
Давайте возьмем координатный луч.
На нем отмечено начало – точка О, единичный отрезок и справа от начала координат у нас находятся положительные числа в порядке возрастания.
А где расположить отрицательные?
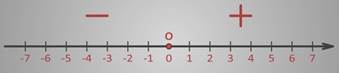
Чтобы отметить отрицательные числа нужно луч дополнить противоположным ему лучом и нанести на него такие же деления.
Таким образом, получилась координатная прямая.
Справа от точки О – начала координат – находятся положительные числа, а слева – отрицательные.
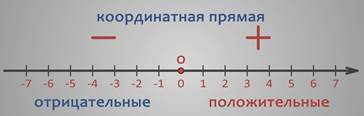
Следовательно, координатная прямая – это прямая с указанным на ней началом отсчета, направлением отсчета и единичным отрезком.
Координата – число, показывающее положение точки на координатной прямой.
Числа, расположенные справа от точки О на координатной прямой – положительные, соответственно направление, в котором они расположены называют положительным.
Числа, которые расположены слева – отрицательные, поэтому направление, в котором они расположены называется отрицательным.
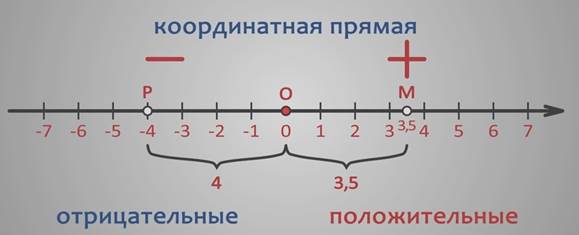
На координатной прямой стрелкой указывается только положительное направление. Число 0 разделяет положительные и отрицательные числа.
Каждому числу соответствует единственная точка прямой.
Например, числу 3,5 соответствует точка М, которая удалена от начала отсчета, т. е. от точки О, на расстояние, равное 3,5 (в заданном масштабе), и отложена от точки О в заданном (положительном) направлении.
Верно и обратное: каждая точка координатной прямой соответствует единственному числу.
В таких случаях соответственно говорят «ось x», «ось y» или «ось t».
Координатные прямые могут располагаться на плоскости по-разному, не только горизонтально.
Например, шкалу на термометре можно назвать координатной прямой.
Она будет вертикальной.
В этом случае положительные числа будут находиться выше 0, а отрицательные ниже 0.
Выполним практическое задание:
Изобразим координатную прямую.
Для этого начертим прямую, отметим на ней начало координат – точку О, выберем единичный отрезок, нанесем деления справа и слева от 0, покажем стрелкой направление отсчета, назовем координатную прямую «осью х».
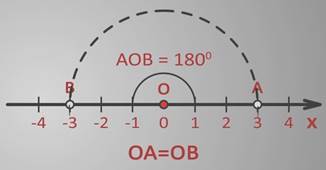
Отметим на координатной прямой точки А (3), В (-3).
Обратите внимание: расстояние от точки А до начала координат точки О будет равно расстоянию OB.
точки А и В будут центрально-симметричны относительно начала отсчета координатной прямой точки О (0).
Следует отметить, что центром симметрии точек на координатной прямой может быть любая точка данной прямой.
Поучимся находить симметричные точки на координатной прямой.
Пусть точка О (0) – центр симметрии.
Найдем точку, симметричную точке С (-6).
Такой точкой будет точка расположенная по другую сторону от центра симметрии.
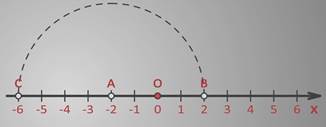
Центром симметрии теперь будет точка А (-2).
Между точками С (-6) и А (-2) – четыре единичных отрезка.
Отсчитаем от точки А (-2) четыре единичных отрезка вправо отметим точку В.
Определим ее координату – (2).
Таким образом, точки С (-6) и В (2) будут центрально-симметричны относительно точки А (-2).
А как определить координату центра симметрии двух точек на координатной прямой?
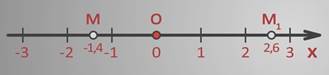
Пусть даны симметричные точки М(-1,4) и М1(2,6).
Расстояние от точки М до О(0) 1,4, от М1 до начала координат – 2,6.
Центр симметрии должен быть посередине.
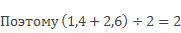
Таким образом, в этом уроке Вы узнали, что такое координатная прямая, научились определять координаты точек и находить симметричные точки.
Прямоугольная система координат. Ось абсцисс и ординат
Прямоугольная декартова система координат
Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
Прямоугольная система координат в трехмерном пространстве
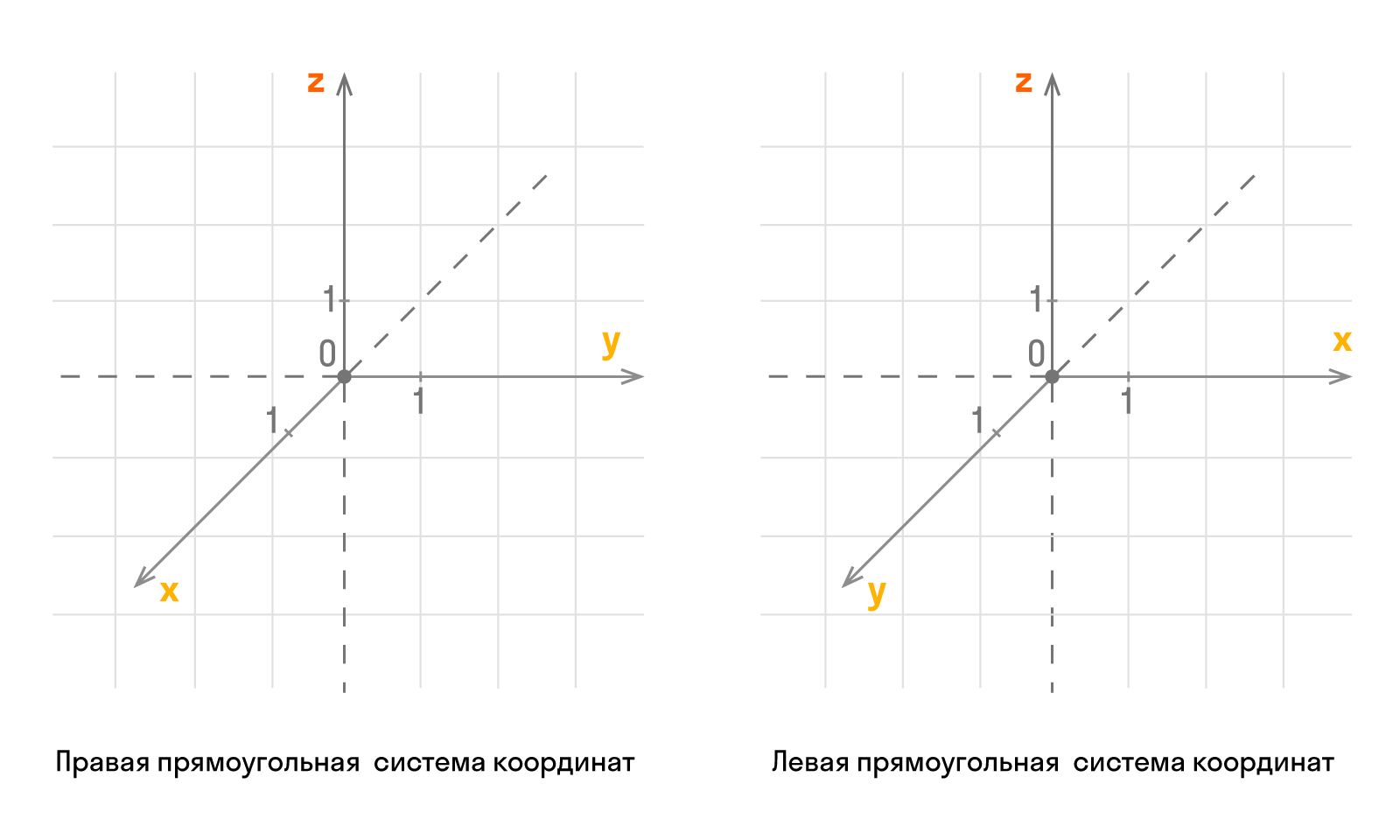
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.
Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.
Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Координаты точки в трехмерном пространстве
Сформулируем определение точки М в трехмерном пространстве.
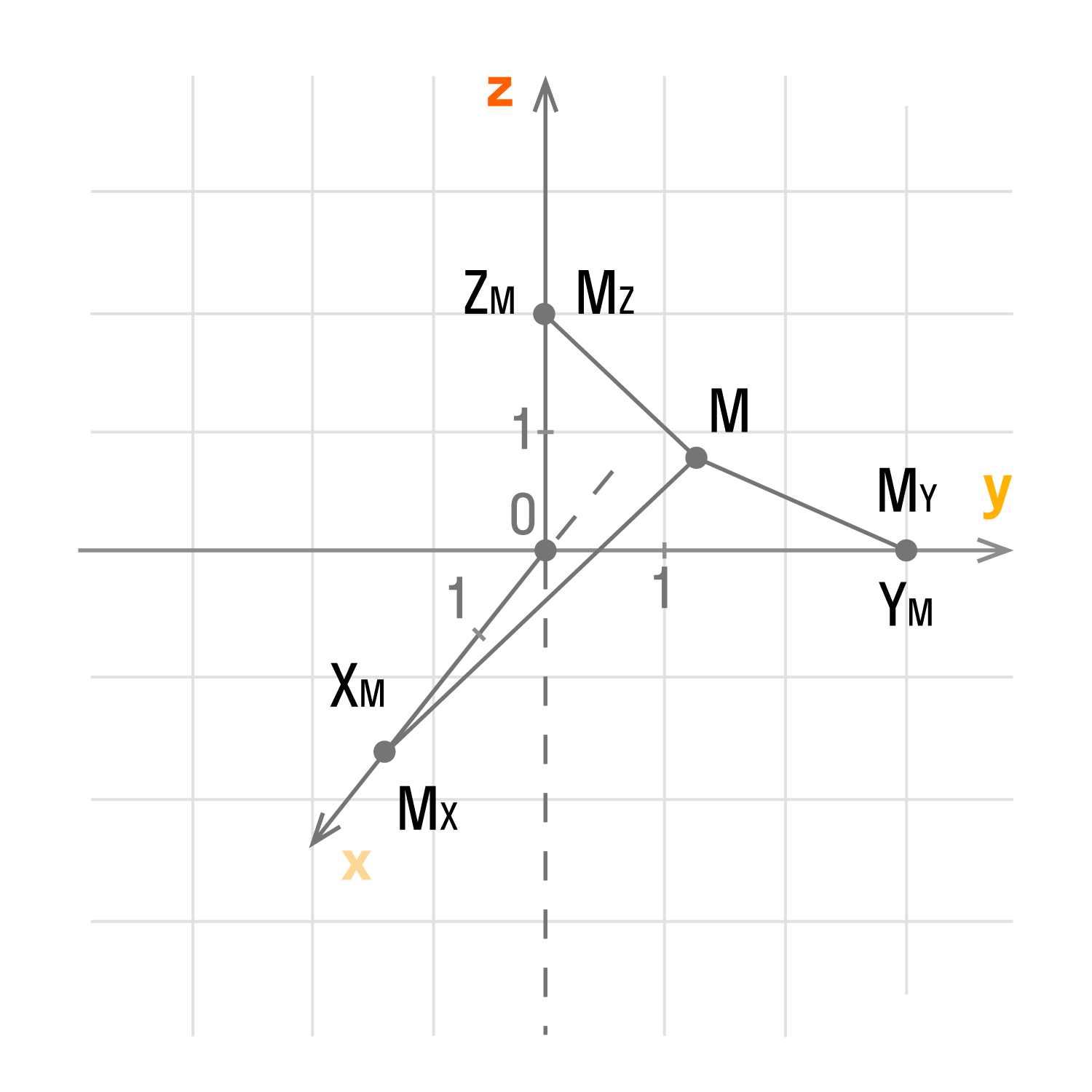
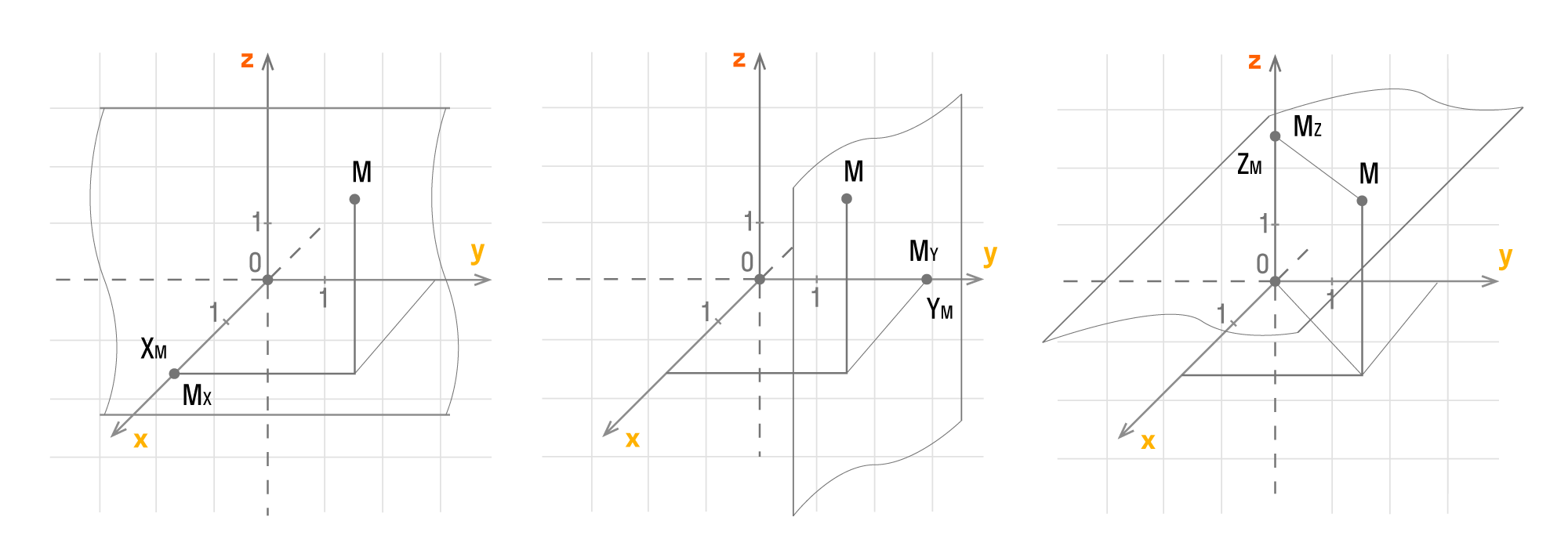
Пусть Mx, My, Mz — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения xM, yM, zM. Как это выглядит на координатных прямых:
Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в Mx, My, Mz.
У каждой точки трехмерного пространства есть свои данные (xM, yM, zM), которые являются координатами точки М.
xM, yM, zM — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (xM, yM, zM) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.
Координатная прямая (числовая прямая), координатный луч
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.
Координатный луч
Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.
На примере мы видим, что O является началом луча.
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.
Координатный луч – это шкала, которая может длиться до бесконечности.
Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.
Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.
Координатная прямая
Проведите луч в противоположную сторону, дополнив его до прямой
Отложите единичные отрезки по примеру, указанному выше
Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.
Соответствие между точками координатной прямой и действительными числами
Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.
Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.
Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.
Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.
Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.
Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.
Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.
Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.
Благодаря этому утверждению координатную прямую зачастую определяют как числовую.
Координаты точек на координатной прямой
Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.