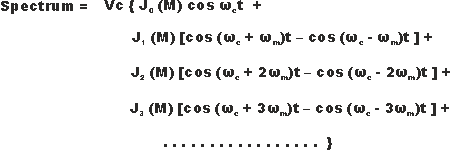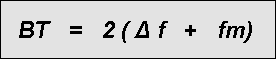что такое полоса модуляции
Что такое частотная модуляция Ширина полосы частот, Спектр и боковых полос?
— Замечания и детали частотной модуляции полосы пропускания, спектра и боковых полос, а также их влияние на использование FM.
Ширина полосы частот, спектр и боковые полосы имеют большое значение при использовании частотной модуляции.
Боковые полосы модулированного сигнала частоты простираются по обе стороны от основной несущей, и привести к пропускной способности общего сигнала, чтобы увеличить далеко за рамки этого немодулированной несущей.
По мере того как модуляция несущей изменяется, так что боковые полосы и, следовательно, пропускную способность и общий спектр сигнала.
Частотная модуляция Функции Бесселя и боковые полосы
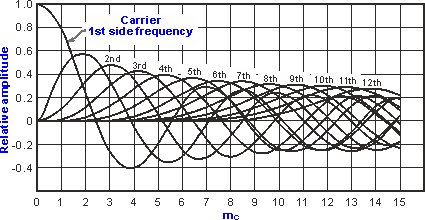
Полный спектр можно видеть, состоит из носителя плюс бесконечное число боковых полос распространяющейся по обе стороны от несущей при целых кратных частоте модуляции. Относительные уровни боковых полос можно получить, обратившись к таблице функций Бесселя. Как видно из изображения ниже, что относительные уровни поднимаются и опускаются в соответствии с различными значениями индекса модуляции.
Относительные уровни несущей и боковых полос для частотно-модулированного сигнала
При малых значениях индекса модуляции, при использовании узкополосного FM, и сигнал FM состоит из несущей и двух боковых полос, разнесенных на частоте модуляции по обе стороны от несущей. Это выглядит таким же, как сигнал АМ, но разница в том, что нижняя боковая полоса находится вне фазы 180 градусов.
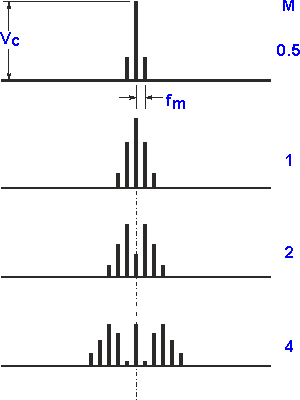
По мере увеличения индекса модуляции обнаруживается, что другие боковые полосы с удвоенной частотой модуляции начинают появляться. По мере увеличения индекса другие дополнительные боковые полосы можно также увидеть.
Спектры сигнала FM с различными уровнями индекса модуляции
При определенных уровнях модуляции, где индекс модуляции равен фигуры 2.41, 5.53, 8.65 и других высших конкретных уровней, носитель падает на фактические цифры фигуры нулю, то сигнал, состоит просто из боковых полос.
полоса модуляции частоты
В случае с амплитудно-модулированным сигналом необходимая полоса пропускания в два раза превышает максимальную частоту модуляции. Несмотря на то, то же самое справедливо и для узкополосного сигнала FM, ситуация не верно для широкополосного сигнала FM. Здесь требуемая пропускная способность может быть очень большим, с обнаруживаемые боковые полосы разводя на больших количеств частотного спектра. Обычно необходимо, чтобы ограничить ширину полосы сигнала, таким образом, чтобы он не ненужных помех станциям обеих сторон.
В качестве частотно-модулированный сигнал имеет боковые полосы, которые простираются до бесконечности, нормально принятой практикой, чтобы определить пропускную способность, что и который содержит приблизительно 98% от мощности сигнала.
Правило большого пальца, часто называют Правило Карсон утверждает, что 98% мощности сигнала содержится в полосе частот, равной частоте отклонения, плюс частота модуляции в два раза, то есть:
Ключевые моменты для ширины полосы частот модуляции и боковых полос
Есть несколько интересных точек по отношению к суммарной ширине полосы частот модуляции:
• Ширина полосы частот модулированного сигнала изменяется как с отклонением частоты и коэффициента модуляции.
• Увеличение частоты модуляции увеличивает разделение частот между боковыми полосами.
• частота полосы пропускания модуляции возрастает с увеличением частоты модуляции, но не прямо пропорционально ему.
ширина полосы частот модуляции имеет важное значение, как это с какой-либо другой формы сигнала. С группой занятости растет, и давление на пространстве спектра, необходимо обеспечить полосу пропускания частоты модулированного сигнала находящиеся в его указанной надбавки. Любое неправомерное распространение сигнала за пределами этого, вероятно, вызовет помехи другим пользователям.
Что такое частотная модуляция Ширина полосы частот, Спектр и боковых полос?
— Замечания и детали частотной модуляции полосы пропускания, спектра и боковых полос, а также их влияние на использование FM.
Ширина полосы частот, спектр и боковые полосы имеют большое значение при использовании частотной модуляции.
Боковые полосы модулированного сигнала частоты простираются по обе стороны от основной несущей, и привести к пропускной способности общего сигнала, чтобы увеличить далеко за рамки этого немодулированной несущей.
По мере того как модуляция несущей изменяется, так что боковые полосы и, следовательно, пропускную способность и общий спектр сигнала.
Частотная модуляция Функции Бесселя и боковые полосы
Полный спектр можно видеть, состоит из носителя плюс бесконечное число боковых полос распространяющейся по обе стороны от несущей при целых кратных частоте модуляции. Относительные уровни боковых полос можно получить, обратившись к таблице функций Бесселя. Как видно из изображения ниже, что относительные уровни поднимаются и опускаются в соответствии с различными значениями индекса модуляции.
Относительные уровни несущей и боковых полос для частотно-модулированного сигнала
При малых значениях индекса модуляции, при использовании узкополосного FM, и сигнал FM состоит из несущей и двух боковых полос, разнесенных на частоте модуляции по обе стороны от несущей. Это выглядит таким же, как сигнал АМ, но разница в том, что нижняя боковая полоса находится вне фазы 180 градусов.
По мере увеличения индекса модуляции обнаруживается, что другие боковые полосы с удвоенной частотой модуляции начинают появляться. По мере увеличения индекса другие дополнительные боковые полосы можно также увидеть.
Спектры сигнала FM с различными уровнями индекса модуляции
При определенных уровнях модуляции, где индекс модуляции равен фигуры 2.41, 5.53, 8.65 и других высших конкретных уровней, носитель падает на фактические цифры фигуры нулю, то сигнал, состоит просто из боковых полос.
полоса модуляции частоты
В случае с амплитудно-модулированным сигналом необходимая полоса пропускания в два раза превышает максимальную частоту модуляции. Несмотря на то, то же самое справедливо и для узкополосного сигнала FM, ситуация не верно для широкополосного сигнала FM. Здесь требуемая пропускная способность может быть очень большим, с обнаруживаемые боковые полосы разводя на больших количеств частотного спектра. Обычно необходимо, чтобы ограничить ширину полосы сигнала, таким образом, чтобы он не ненужных помех станциям обеих сторон.
В качестве частотно-модулированный сигнал имеет боковые полосы, которые простираются до бесконечности, нормально принятой практикой, чтобы определить пропускную способность, что и который содержит приблизительно 98% от мощности сигнала.
Правило большого пальца, часто называют Правило Карсон утверждает, что 98% мощности сигнала содержится в полосе частот, равной частоте отклонения, плюс частота модуляции в два раза, то есть:
Ключевые моменты для ширины полосы частот модуляции и боковых полос
Есть несколько интересных точек по отношению к суммарной ширине полосы частот модуляции:
• Ширина полосы частот модулированного сигнала изменяется как с отклонением частоты и коэффициента модуляции.
• Увеличение частоты модуляции увеличивает разделение частот между боковыми полосами.
• частота полосы пропускания модуляции возрастает с увеличением частоты модуляции, но не прямо пропорционально ему.
ширина полосы частот модуляции имеет важное значение, как это с какой-либо другой формы сигнала. С группой занятости растет, и давление на пространстве спектра, необходимо обеспечить полосу пропускания частоты модулированного сигнала находящиеся в его указанной надбавки. Любое неправомерное распространение сигнала за пределами этого, вероятно, вызовет помехи другим пользователям.
Что такое полоса модуляции
Амплитудная модуляция (AM) — наиболее распространенный тип модуляции. В системе с AM амплитуда несущей изменяется в соответствии с изменением сигнала или информации (рис. 14.1). В отсутствие сигнала амплитуда несущей имеет постоянный уровень, как показано на рис. 14.1(б). При модуляции синусоидальным сигналом амплитуда несущей увеличивается или уменьшается относительно своего немодулированного уровня по синусоидальному закону в соответствии с нарастанием или спаданием модулирующего сигнала. Чем больше амплитуда модулирующего сигнала, тем сильнее изменяется амплитуда несущей. Амплитудно-модулированная несущая (рис. 14.1(в)) имеет огибающую, в точности повторяющую форму модулирующего сигнала, и при демодуляции именно эта огибающая выделяется как полезный сигнал.
Глубина модуляции
Отношение амплитуды модулирующего сигнала к амплитуде несущей называется глубиной или коэффициентом модуляции. Она определяет меру изменения уровня несущей при модуляции. Глубина модуляции всегда выражается в процентах, и поэтому о ней говорят как о «процентной» модуляции.
Амплитуда сигнала
Глубина модуляции = ——————————— • 100%
Амплитуда несущей
(см. рис. 14.1). Например, если амплитуда сигнала равна 1 В, а амплитуда несущей — 2 В, то глубина модуляции составляет (1 В)/(2 В) • 100% = 50%. Такую глубину модуляции имеет АМ-несущая, показанная на рис. 14.1.
Рис. 14.1. Амплитудная модуляция (глубина модуляции 50%);
(а) сигнал; (б) несущая; (в) модулированная несущая.
Перемодуляция
На рис. 14.2(а) показана АМ-несущая со 100%-ной глубиной модуляции. Глубина модуляции, превышающая 100%, приводит к искажениям (рис. 14.2(б)). По этой причине глубину модуляции ограничивают. Например, при передачах радиостанции Би-би-си она ограничена величиной 80%.
Рис. 14.2. (а) Модуляция 100%; (б) перемодуляция.
Боковые частоты
Можно показать, что амплитудно-модулированная несущая состоит из трех гармонических (синусоидальных) компонент с постоянными амплитудами и разными частотами. Этими тремя компонентами являются: сама несущая и два сигнала боковых частот f1 и f2. Каждый модулирующий гармонический сигнал порождает две боковые частоты. Пусть fs – частота модулирующего сигнала и fc – частота несущей, тогда
f1 = fc – fs, f2 = fc + fs,
где f1 и f2 – так называемые нижняя боковая и верхняя боковая частоты соответственно. Например, если частота несущей равна 100 кГц, а частота сигнала — 1 кГц, то
Нижняя боковая частота f1 = 100 – 1 = 99 кГц,
Верхняя боковая частота f2 = 100 + 1 = 101 кГц.
Амплитудно-модулированная несущая, т. е. несущая вместе с двумя сигналами боковых частот, может быть представлена в виде трех вертикальных стрелок, каждая из которых соответствует одному гармоническому сигналу (рис. 14.3). То, что изображено на этом рисунке, называется частотным спектром сигнала (в данном случае частотным спектром АМ-несущей).
Рис. 14.3. Частотный спектр AM-несущей. Рис. 14.4. Боковые полосы.
Боковые полосы
Информационные сигналы почти всегда имеют сложную форму и состоят из большого числа гармонических сигналов. Поскольку каждый гармонический сигнал порождает пару боковых частот, то сложный негармонический сигнал будет порождать многочисленные боковые частоты, что приведет к образованию двух полос частот по обе стороны от несущей (рис. 14.4). Это так называемые боковые полосы частот. Область частот между наибольшей верхней боковой частотой f2 и наименьшей верхней боковой частотой f4 называют верхней боковой полосой (ВБП). Аналогично область частот между наибольшей нижней боковой частотой f3 и наименьшей нижней боковой частотой f1 называют нижней боковой полосой (НБП).
Эти две боковые полосы расположены симметрично относительно несущей, и каждая из них содержит одну и ту же информацию. Несущая не несет никакой информации. Всю информацию несут боковые частоты.
При модуляции одиночным гармоническим сигналом принимается, что верхняя и нижняя боковые полосы простираются от несущей до верхней и нижней боковых частот соответственно (рис. 14.5).
Пример 1
Несущая с частотой 100 кГц промодулирована по амплитуде сигналом, занимающим полосу частот 400-3400 Гц. Определите ширину боковых полос.
Решение
Частота 400 Гц, самая низкая в спектре сигнала, порождает еще две боковые частоты:
Ширина полосы частот
Другими словами, в данном случае ширина полосы частот, занимаемой амплитудно-модулированной несущей, равна удвоенной частоте модулирующего сигнала.
В случае передачи сложного сигнала ширина полосы частот, занимаемой АМ-системой передачи информации, равна удвоенной наивысшей частоте в спектре модулирующего сигнала и, таким образом, включает в себя все боковые частоты.
Одно- и двухполосная передача
Поскольку одна боковая полоса содержит столько же информации, сколько и другая, передачу можно осуществлять с использованием только одной боковой полосы, и при этом не будет никакой потери информации. При однополосной передаче (SSB — по связной терминологии) одна из боковых полос — или нижняя, или верхняя — подавляется и передается только одна оставшаяся боковая полоса. При двухполосной (DSB) передаче передаются обе боковые полосы.
Однополосная передача занимает лишь половину той полосы частот, которая используется при двухполосной передаче, и по этой причине она применяется в телефонии и радиосвязи. При однополосной передаче в заданном диапазоне частот несущей можно расположить вдвое большее число информационных каналов, чем при двухполосной передаче. В силу простоты двухполосная передача используется всеми радиовещательными системами с AM. Поэтому, когда речь идет о связи с использованием AM, обычно имеется в виду двухполосная передача, если не оговорено обратное.
Пример 2
Несущая промодулирована по амплитуде периодическим сигналом в виде меандра с частотой 100 Гц. Пренебрегая гармониками выше пятой, установите ширину полосы частот, необходимую а) для DSB (двухполосной)-передачи и б) для SSB (однополосной)-передачи.
Решение
Сигнал в виде меандра с частотой 100 Гц содержит следующие гармоники:
основную гармонику =100 Гц,
гармонику 3-го порядка = 3 • 100 = 300 Гц,
гармонику 5-го порядка = 5 • 100 = 500 Гц.
Гармониками более высокого порядка пренебрегаем. Таким образом, в обрезанном спектре модулирующего сигнала максимальная частота fмакс = 500 Гц.
Ширина полосы для DSB-передачи = 2 • fмакс = 2•500 = 1000 Гц.
Ширина полосы для SSB-передачи = DSB/2 = 1000/2 = 500 Гц.
В этом видео рассказывается об амплитудной модуляции:
Теория радиоволн: аналоговая модуляция
Амплитудная модуляция
При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.
Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.
Данный спектр свойственен для модулирующего колебания постоянной частоты.
На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции
Что такое полоса модуляции
Сокращенное название однополосной модуляции (SSB), принятое в радиолюбительском коде, происходит от английского Single Side Band, что в переводе означает — одна боковая полоса.
Прежде чем приступить к рассмотрению однополосной модуляции, вспомним, что представляет собой модуляция вообще. При этом мы не будем пока касаться методов ее осуществления.
Модуляцией называется процесс изменения одного или нескольких параметров данного сигнала под воздействием другого сигнала.
Модулируемый сигнал обычно представляет собой простейшие колебания, которые описываются выражением: u=Ucos( w ot+ f o), где U — амплитуда; w o=2 p fo — угловая частота; f o — начальная фаза; t — время.
Параметрами такого сигнала являются амплитуда U, частота w о (или fo) и фаза f o.
Низкочастотный сигнал X(t), воздействующий на один из этих параметров, называется модулирующим сигналом. В зависимости от того, на какой из параметров воздействует такой сигнал, различают три вида модуляции: амплитудную, частотную и фазовую.
Для анализа модулированных колебаний будем пользоваться тремя различными представлениями о сигнале: временным, спектральным (частотным) и векторным. В соответствии с этими представлениями косинусоидальное (или синусоидальное) колебание, записанное выше, — графически можно представить так, как показано на рис. 1.
Рис. 1. Графическое изображение простейшего колебания:
а—временная диаграмма (осциллограмма);
б — спектральная (частотная) диаграмма;
в — векторная диаграмма
Следует отметить, что все три представления о модулирующем сигнале совершенно равносильны. Мы будем пользоваться каждым из них или несколькими представлениями параллельно, когда это окажется наиболее подходящим.
Рассмотрим амппитудную модуляцию. В этом случае амплитуда U высокочастотных колебаний изменяется во времени в соответствии с передаваемым низкочастотным сигналом Um=U+dUx(t), где dU—постоянная величина, характеризующая интенсивность воздействия модулирующего сигнала на амплитуду. Подставив в первое выражение значение амплитуды Um, получим
Отношение dU/U=m, характеризующее глубину модуляции, называется коэффициентом модуляции.
Если модулирующий сигнал изменяется по закону
где W =2 p F, F — частота модулирующего сигнала, то, считая начальную фазу f o равной нулю, можно записать
u=U(1+m cos W t)cos w ot.
Раскрыв скобки и проведя преобразование, получим
Последнее равенство представляет собой сумму трех косинусоидальных колебаний, а именно, первоначальное колебание (без учета фазы f o) с частотой fo, или так называемая несущая колебания с частотой fo+F, верхняя боковая частота и колебания с частотой fo—F, нижняя боковая частота. Амплитуды боковых колебаний равны между собой и пропорциональны амплитуде несущей и коэффициенту модуляции.
На рис. 2, а показаны временные, спектральные и векторные диаграммы модулирующего и модулированного сигналов, как видно из рис. 2, б огибающая модулированного колебания полностью повторяет первоначальный сигнал.
Рис. 2. Диаграммы модулирующего и модулированного сигнала:
а — временная диаграмма модулирующего сигнала;
б — временная диаграмма амплитудно-модулированного сигнала;
в, г,д,е — спектральные (частотные) и векторные диаграммы.
Рис. 3. Векторная диаграмма амплитпудномодулированного сигнала одним тоном
При частотной и фазовой модуляции длина вектора U остается постоянной. Изменяется во времени его положение на плоскости. Вектор как бы качается относительно первоначального положения. Угол отклонения dф называется девиацией фазы. Отклонение частоты df от своего номинального значения fo называется девиацией частоты.
Разница между частотной и фазовой модуляцией заключается в том, что при фазовой модуляции мгновенное изменение фазового угла происходит по закону изменения низкочастотного сигнала, а при частотной модуляции по такому закону изменяется мгновенная частота. Определить, является ли данный сигнал частотномодулированным или фазо-модулированным, можно только в том случае, если известен закон изменения низкочастотного сигнала. Между обоими видами модуляции существует вполне определенная математическая зависимость. В обоих случаях вектор, соответствующий модулированному сигналу, вращается вокруг своего начала не равномерно, а с некоторой переменной угловой скоростью.
Исследование сигналов AM колебаний показывает, что полезная информация заключается в любой из двух боковых полос модуляции, а несущая никакой полезной информации не имеет. В передатчике на несущую тратится значительная часть мощности, что делает AM модуляцию малоэффективной.
Очевидно, для передачи нужной информации можно ограничиться передачей только одной из боковых полос. Несущую можно восстанавливать в приемнике с помощью местного маломощного гетеродина. При этом будет экономиться не только энергия, затрачиваемая на питание передатчика, но и сузится полоса частот, занимаемая сигналом.
Некоторый интерес представляют собой также передача двух боковых полос без несущей (DSB) и одной боковой с несущей. Поэтому, рассматривая однополосную модуляцию (ОМ), затронем также и эти виды модуляции.
На рис. 5 представлена частотная диаграмма первоначального спектра перепеваемого сигнала, AM, DSB, SSB с несущей и SSB без несущей. Однополосный сигнал может быть образован с сохранением взаимного расположения частотных составляющих спектра, как показано на рис. 5,е и 5, г или с переворачиванием (инверсией) спектра (рис. 5,д и 5,ж). В первом случае однополосный спектр сигнала называют верхней боковой полосой или нормальным спектром, во втором случае — нижней боковой или инвертированным спектром.
Рис. 5. Спектральные диаграммы
На рис.6 приведены векторные диаграммы AM, DSB, SSB с несущей и SSB без несущей при модуляции спектром, состоящим из двух частотных составляющих W 1 и W 2. Вектор несущей заторможен. При AM (рис. 6,а) имеем вектор несущей и две пары векторов, соответствующих двум верхним и двум нижним боковым частотам. Результирующий вектор совпадает по фазе с вектором несущей.
Рис. 6. Векторные диаграммы при модуляции двумя тонами: а — амплитудная модуляция (AM);
б— двухполосная модуляция с подавлением несущей; в — однополосная мо-дчляция (ВВП) с несущей;
г — однопо-.юсная модуляция (ВВП) без несущей.
При DSB (рис. 6,б) отсутствует вектор несущей. Поэтому результирующий вектор либо совпадает с вектором подавленной несущей, либо направлен в противоположную сторону, т. е. сдвинут по фазе на 180°. На рисунке показан случай, когда результирующий вектор как раз направлен в противоположную сторону.
На рис.6,г дана векторная диаграмма однополосного двухтонального сигнала. Результирующий вектор в этом случае представляет собой вектор, вращающийся со скороростью ( W 1+ W 2)/2 против часовой стрелки. Так как один из векторов все время «догоняет» другой, то амплитуда результирующего вектора изменяется. Отсюда можно сделать также вывод, что однополосная модуляция представляет собой комбинированную амплитудно-частотную модуляцию. Исследования показывают, что при однополосной модуляции амплитуда изменяется по закону изменения мгновенных амплитуд модулирующего сигнала, а частота — по закону изменения его мгновенной частоты.
Очень важную практическую роль играют временные характеристики рассмотренных выше сигналов, поскольку с ними приходится сталкиваться при налаживании SSB возбудителей с помощью осциллографа. Поэтому рассмотрим подробно сначала временные характеристики при модуляции одним тоном (рис. 7), а затем двумя тонами (рис. 8).
Рис. 7. Временные характеристики при модуляции одним тоном: а — исходный низкочастотный сигнал;
б — амплитудная модуляция (AM); в — двухполосная модуляция с подавлением несущей; г — однополосная модуляция с несущей;
д — однополосная модуляция.
Исходный синусоидальный сигнал низкой частоты показан на рис.7,а. Диаграмму AM сигнала (рис. 7,б) легко построить, пользуясь векторной диаграммой рис.3. Фаза огибающей AM сигнала совпадает с фазой исходного сигнала в течение всего периода модуляции.
На рис.7,в приведена диаграмма двухполосного сигнала, построенная в соответствии с рис.2, но при векторе несущей, равном нулю. Вращающиеся в противоположные стороны векторы дважды за один оборот (за период Т=1/F) складываются арифметически и дважды компенсируют друг друга. Поэтому модуль результирующего вектора изменяется синусоидально, а фаза в течение одной половины периода модулирующего сигнала совпадает с фазой подавленной несущей, в течение же другой половины — опрокидывается. Так как амплитуда — величина положительная, то огибающая двухполосного сигнала без несущей представляет собой синусоиду, отрицательная половина которой повернута на 180° вокруг оси времени. Высокочастотное заполнение осциллограммы представляет собой колебание с частотой fo, фаза которого опрокидывается при переходе модулирующего напряжения через ноль.
Пользуясь той же векторной диаграммой AM колебания, но отбросив один из векторов, соответствующей боковой частоте, можно легко построить осциллограмму однополосного сигнала с несущей. Огибающая в этом случае так же не соответствует первоначальному сигналу, причем искажения огибающей будут тем больше, чем глубже модуляция. На рисунке пунктиром показана огибающая при стопроцентной модуляции. Частота заполнения изменяется в течение периода низкой частоты.
На рис.7,д изображена диаграмма однополосного сигнала без несущей. Диаграмма представляет собой обычный синусоидальный сигнал, (огибающая прямая линия), с постоянной амплитудой, с частотой w o+F или w o—F. Чем глубже модуляция, тем больше амплитуда сигнала.
Рассмотрим временные диаграммы двухчастотного сигнала. Для упрощения построения возьмем два сигнала с одинаковой амплитудой и кратными частотами F1 и F2=3F1. На рис.8,а сплошной линией представлен модулирующий сигнал, в состав которого входят колебания с указанными частотами. На рис.8,б показана диаграмма амплитудно-модулированного сигнала. Его огибающая соответствует модулирующему сигналу.
Рис. 8. Временные диаграммы сигналов: а—модулирующего двухчастотного; б — сигнала AM;
в — двухполосного без несущей; г — однополосного без несущей
Диаграмму двухполосного сигнала без несущей (рис. 8,в) можно построить рассуждая так же, как в случае одночастотного сигнала. В течение тех промежутков времени, когда модулирующее напряжение положительно, фаза огибающей соответствует фазе модулирующего напряжения, а фаза высокочастотного заполнения совпадает с фазой подавленной несущей. При отрицательном модулирующем напряжении фазы огибающей и высокочастотного заполнения опрокидываются. Частота заполнения в обеих случаях равна частоте несущей f0. Временную диаграмму двухтонального однополосного сигнала можно построить и проанализировать, обратившись к соответствующей диаграмме рис.6. В нашем случае вектора, вращающиеся со скоростью W 1=2 p F1, и W 2=2 p (3F1)=3 W 1 имеют одинаковую амплитуду, поэтому результирующий вектор будет вращаться равномерно со скоростью
В начальный момент, когда оба вектора совпадают, длина результирующего вектора будет максимальной. Следовательно, амплитуда огибающей будет иметь удвоенную величину относительно амплитуд каждой из высокочастотных составляющих. В течение одного оборота вектора, угловая скорость которого W 1, вектор с угловой скоростью W 2= W 3, дважды «догонит» первый вектор и два раза окажется направленным в противоположную сторону. В соответствии с этим длина результирующего вектора за период T1=1/F три раза окажется равной удвоенной амплитуде высокочастотных колебаний и два раза равной нулю.
Временная диаграмма для данного случая показана на рис.8,г. Частота высокочастотного заполнения равна fo+F3=fo+2F1. Необходимо отметить, что в спектре колебаний, показанных на рис.8,в колебания с частотой «заполнения», т. е. с частотой несущей, отсутствуют. Также нет в составе спектра сложного колебания, временная диаграмма которого изображена на рис.8,г, составляющей частоты fo+2F.
При амплитудном детектировании рассмотренных выше сигналов на выходе детектора будет напряжение, соответствующее огибающей высокочастотных колебаний. В случае AM огибающая повторяет исходный сигнал, поэтому на выходе детектора появится модулирующий первоначальный сигнал низкой частоты. Детектирование однополосного сигнала с несущей также приведет к появлению на выходе детектора напряжения, соответствующего огибающей. Но, так как сама огибающая не точно воспроизводит модулирующий сигнал, то и продуктом детектирования будет сигнал искаженный, причем, чем глубже модуляция, тем больше искажения.
Ясно, что обычное детектирование DSB или SSB даст одни искажения. Например, при модуляции одним тоном F детектирование DSB приведет к появлению сигнала с удвоенной частотой 2F1, и его гармоник, а детектирование SSB даст только постоянную составляющую.
Рис. 9. Векторная диаграмма при детектировании двухполосного сигнала без несущей
Детектирование SSB с восстановленной в приемнике несущей в принципе не отличается от детектирования однополосного сигнала с неподавленной несущей.
Однако на форму выходного сигнала (огибающей) в этом случае, как было выяснено выше, влияет соотношение между амплитудой сигнала гетеродина и амплитудой детектируемого сигнала. Очевидно, искаже4 ния будут незначительны, когда амплитуда напряжения гетеродина во много раз будет больше амплитуды детектируемого сигнала. В этом можно убедиться, рассматривая временную диаграмму однополосного сигнала с неподавленной несущей (рис.7,г).