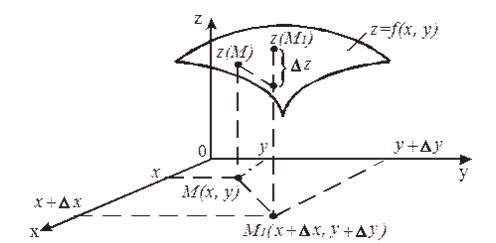
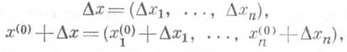что такое полное приращение
Полное приращение
Смотреть что такое «Полное приращение» в других словарях:
приращение — [сокращение] ширины штриха : Степень увеличения [уменьшения] ширины штриха символа штрихового кода, обусловленная процессами воспроизведения и способами печати Источник: ГОСТ 30721 2000: Автоматическая идентификация. Кодирование штриховое.… … Словарь-справочник терминов нормативно-технической документации
приращение абсолютной продольной (поперечной) деформации образца — приращение абсолютной продольной (поперечной) деформации образца … Справочник технического переводчика
Приращение абсолютной продольной (поперечной) деформации образца — Dl1,Dl2 Полное укорочение (удлинение) линейных абсолютных размеров образца в пределах базы измерения деформации вдоль (поперек) образующей, вызванное осевой сжимающей силой Источник: ГО … Словарь-справочник терминов нормативно-технической документации
Приращение абсолютной продольной (поперечной) деформации образца — – бет. полное укорочение (удлинение) линейных абсолютных размеров образца в пределах базы измерения деформации вдоль (поперек) образующей, вызванное осевой сжимающей силой. [ГОСТ 24452 80] Рубрика термина: Испытания бетона Рубрики… … Энциклопедия терминов, определений и пояснений строительных материалов
ПЛЯЦЕНТА — ПЛЯЦЕНТА. Содержание: I. Сравнительная анатомил. 55. 1 II. Развитие П. у человека. 556 III. Плацента доношенного плодного яйца. 5Е8 IV. Физиология и биология 11. 55а V. Патология П. Пат. формы II. j … Большая медицинская энциклопедия
Термодинамика — наука о наиболее общих свойствах макроскопических систем, находящихся в состоянии термодинамического равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундаментальных принципов (начал), которые являются… … Большая советская энциклопедия
ТЕРМОДИНАМИКА — наука о наиб. общих св вах макроскопич. физ. систем, находящихся в состоянии термодинамич. равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундам. принципов (начал), к рые явл. обобщением многочисл. наблюдений и… … Физическая энциклопедия
Теплота — 1) Т. мы называем причину, вызывающую в нас специфические, всем известные тепловые ощущения. Источником этих ощущений являются всегда какие либо тела внешнего мира, и, объективируя наши впечатления, мы приписываем этим телам содержание некоторого … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия
ПОЛНОЕ ПРИРАЩЕНИЕ
Смотреть что такое «ПОЛНОЕ ПРИРАЩЕНИЕ» в других словарях:
Полное приращение — приращение, приобретаемое функцией нескольких переменных, когда все аргументы получают (вообще говоря, не нулевые) приращения Δx1, Δx2. Δxn. При некоторых условиях (например, если все частные производные непрерывны) П. п. можно… … Большая советская энциклопедия
приращение — [сокращение] ширины штриха : Степень увеличения [уменьшения] ширины штриха символа штрихового кода, обусловленная процессами воспроизведения и способами печати Источник: ГОСТ 30721 2000: Автоматическая идентификация. Кодирование штриховое.… … Словарь-справочник терминов нормативно-технической документации
приращение абсолютной продольной (поперечной) деформации образца — приращение абсолютной продольной (поперечной) деформации образца … Справочник технического переводчика
Приращение абсолютной продольной (поперечной) деформации образца — Dl1,Dl2 Полное укорочение (удлинение) линейных абсолютных размеров образца в пределах базы измерения деформации вдоль (поперек) образующей, вызванное осевой сжимающей силой Источник: ГО … Словарь-справочник терминов нормативно-технической документации
Приращение абсолютной продольной (поперечной) деформации образца — – бет. полное укорочение (удлинение) линейных абсолютных размеров образца в пределах базы измерения деформации вдоль (поперек) образующей, вызванное осевой сжимающей силой. [ГОСТ 24452 80] Рубрика термина: Испытания бетона Рубрики… … Энциклопедия терминов, определений и пояснений строительных материалов
ПЛЯЦЕНТА — ПЛЯЦЕНТА. Содержание: I. Сравнительная анатомил. 55. 1 II. Развитие П. у человека. 556 III. Плацента доношенного плодного яйца. 5Е8 IV. Физиология и биология 11. 55а V. Патология П. Пат. формы II. j … Большая медицинская энциклопедия
Термодинамика — наука о наиболее общих свойствах макроскопических систем, находящихся в состоянии термодинамического равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундаментальных принципов (начал), которые являются… … Большая советская энциклопедия
ТЕРМОДИНАМИКА — наука о наиб. общих св вах макроскопич. физ. систем, находящихся в состоянии термодинамич. равновесия, и о процессах перехода между этими состояниями. Т. строится на основе фундам. принципов (начал), к рые явл. обобщением многочисл. наблюдений и… … Физическая энциклопедия
Теплота — 1) Т. мы называем причину, вызывающую в нас специфические, всем известные тепловые ощущения. Источником этих ощущений являются всегда какие либо тела внешнего мира, и, объективируя наши впечатления, мы приписываем этим телам содержание некоторого … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия
Полное приращение и полный дифференциал
Вы будете перенаправлены на Автор24
Записать полное приращение заданной функции
Решение:
По определению полного приращения некоторой функции найдем:
Решение:
По определению полного приращения некоторой функции найдем:
\[\Delta z=(1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]
Готовые работы на аналогичную тему
Для функции трех и более переменных, аналогично как для функции двух переменных определяются полное приращение:
Записать полное приращение заданной функции
Решение:
По определению полного приращения некоторой функции найдем:
Решение:
По определению полного приращения некоторой функции найдем:
\[\Delta z=(1+0,1)\cdot (2+0,1)\cdot (1+0,1)=1,1\cdot 2,1\cdot 1,1=2,541.\]
\[dz=f’_
Записать полный дифференциал заданной функции
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
\[dz=1\cdot \Delta x+2\cdot \Delta y=\Delta x+2\cdot \Delta y.\]
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
\[dz=y\cdot \Delta x+x\cdot \Delta y.\]
Для функции трех и более переменных, аналогично как для функции двух переменных определяются полный дифференциал:
\[dw=f’_
Записать полный дифференциал заданной функции
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
\[dz=z\cdot \Delta x+z\cdot \Delta y+(x+y)\cdot \Delta z.\]
В новых обозначениях выражения для полного дифференциала принимает следующий вид:
Функция, имеющая непрерывные частные производные в заданной точке, является дифференцируемой в данной точке, при этом полный дифференциал функции в данной точке равен сумме произведений частных производных на дифференциалы независимых переменных соответственно.
Записать полный дифференциал заданной функции
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
\[dz=z\cdot dx+0\cdot dy+x\cdot dz=z\cdot dx+x\cdot dz.\]
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
\[dz=y\cdot dx+x\cdot dy.\]
Запишем полный дифференциал в заданной точке:
\[dz|_ <(1,2)>=2\cdot dx+1\cdot dy=2dx+dy.\]
Частное и полное приращение функции
Вы будете перенаправлены на Автор24
Таким образом, имеем:
Записать частные и полное приращение функции
Решение:
По определению частного приращения найдем:
По определению полного приращения найдем:
Готовые работы на аналогичную тему
Решение:
По определению частного приращения найдем:
По определению полного приращения найдем:
\[\Delta _
Проверить утверждение замечания для функции
Решение:
\[\Delta _
\[2\cdot (x+y)+\Delta x+\Delta y\ne x+\Delta x+y+\Delta y,\]
\[\Delta _
Для функции от трех и более переменных, аналогично как для функции двух переменных определяются частные приращения по каждой из переменных:
Записать частные и полное приращение функции
Решение:
По определению частного приращения найдем:
По определению полного приращения найдем:
Решение:
По определению частного приращения найдем:
По определению полного приращения найдем:
\[\Delta _
Полное приращение функции




Полное приращение функции
Производные имеют тенденцию быть производными с правой стороны, принимая во внимание непрерывность, предусмотренную для этих значений переменных, а величины a, p, k стремятся к нулю. Людмила Фирмаль
Кстати об ограничительных отношениях, мы понимаем их в широком смысле и не исключаем возможности того, что эти приращения исчезнут в ходе изменения. Людмила Фирмаль
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института