что такое показатель функции
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №21. Показательная функция.
Перечень вопросов, рассматриваемых в теме:
— какая функция называется показательной;
— какие свойства имеет показательная функция в зависимости от ее основания;
— какой вид имеет график показательной функции в зависимости от ее основания;
— примеры реальных процессов, описываемых показательной функцией.
Функция вида 
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Определение, свойства и график показательной функции
Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.
Для положительного основания значение степени а х можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.
Сформулируем основные свойства показательной функции.
1. Область определения.
Как мы уже сказали, степень а х для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D(y)=R.
2. Множество значений.
Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.
3. Корни (нули) функции.
Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.
При a>1 функция монотонно возрастает.
Рисунок 1 – График показательной функции при a>1
При 0 1 при х стремящемся к минус бесконечности.
2. Рассмотрим пример исследования функции y=–3 х +1.
1) Область определения функции – любое действительное число.
2) Найдем множество значений функции.
Так как 3 х >0, то –3 х х +1 х +1 представляет собой промежуток (-∞; 1).
3) Так как функция y=3 х монотонно возрастает, то функция y=–3 х монотонно убывает. Значит, и функция y=–3 х +1 также монотонно убывает.
4) Эта функция будет иметь корень: –3 х +1=0, 3 х =1, х=0.
Рисунок 3 – График функции y=–3 х +1
6) Для этой функции горизонтальной асимптотой будет прямая y=1.
3. Примеры процессов, которые описываются показательной функцией.
6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.
Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.
Рисунок 4 – График функции y=2 х – изменение количества информации
Примеры и разбор решения заданий тренировочного модуля
Выберите показательные функции, которые являются монотонно убывающими.
Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: 
Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:

Найдите множество значений функции y=3 x+1 – 3.
Так как 3 x+1 >0, то 3 x+1 – 3>–3, то есть множество значений:
Найдите множество значений функции y=|2 x – 2|
2 x –2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2 x – 2|
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №21. Показательная функция.
Перечень вопросов, рассматриваемых в теме:
— какая функция называется показательной;
— какие свойства имеет показательная функция в зависимости от ее основания;
— какой вид имеет график показательной функции в зависимости от ее основания;
— примеры реальных процессов, описываемых показательной функцией.
Функция вида 
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Определение, свойства и график показательной функции
Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.
Для положительного основания значение степени а х можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.
Сформулируем основные свойства показательной функции.
1. Область определения.
Как мы уже сказали, степень а х для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D(y)=R.
2. Множество значений.
Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.
3. Корни (нули) функции.
Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.
При a>1 функция монотонно возрастает.
Рисунок 1 – График показательной функции при a>1
При 0 1 при х стремящемся к минус бесконечности.
2. Рассмотрим пример исследования функции y=–3 х +1.
1) Область определения функции – любое действительное число.
2) Найдем множество значений функции.
Так как 3 х >0, то –3 х х +1 х +1 представляет собой промежуток (-∞; 1).
3) Так как функция y=3 х монотонно возрастает, то функция y=–3 х монотонно убывает. Значит, и функция y=–3 х +1 также монотонно убывает.
4) Эта функция будет иметь корень: –3 х +1=0, 3 х =1, х=0.
Рисунок 3 – График функции y=–3 х +1
6) Для этой функции горизонтальной асимптотой будет прямая y=1.
3. Примеры процессов, которые описываются показательной функцией.
6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.
Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.
Рисунок 4 – График функции y=2 х – изменение количества информации
Примеры и разбор решения заданий тренировочного модуля
Выберите показательные функции, которые являются монотонно убывающими.
Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: 
Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:

Найдите множество значений функции y=3 x+1 – 3.
Так как 3 x+1 >0, то 3 x+1 – 3>–3, то есть множество значений:
Найдите множество значений функции y=|2 x – 2|
2 x –2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2 x – 2|
Что такое показатель функции
График функции имеет следующий вид:
Рассмотрим свойства функции:
Примеры решения задач
Задача 1.
В одной координатной плоскости построить графики функций:
Решение.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y(x) |  |  |  | 1 | 2 | 4 | 8 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = 2 x возрастает на всей области определения D(y)=R, так как основание функции 2 > 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задача 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции 
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y(x) | 8 | 4 | 2 | 1 |  |  |  |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует меньшее значение функции y. Функция 
Подобным образом построим графики остальных функций.
Переменная х может принимать любое значение: D(y)=R, при этом область значений функции: E(y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти область значений функции:
Решение.
Область значений показательной функции y = 2 x – все положительные числа, т. е. 0 x x
2. y = 
умножаем все части двойного неравенства на 3:
из всех частей двойного неравенства вычитаем 5:
11.3.1. Показательная функция, ее свойства и график
Справедливы все свойства степенной функции:
Примеры.
x=0, y=2 0 =1; Точка А.
x=1, y=2 1 =2; Точка В.
x=2, y=2 2 =4; Точка С.
x=3, y=2 3 =8; Точка D.
Большему значению аргумента х соответствует и большее значение функции у. Функция y=2 x возрастает на всей области определения D (y)=R, так как основание функции 2>1.
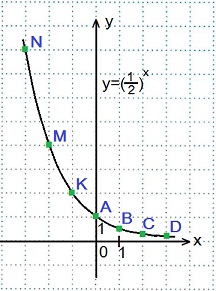
x=1, y=(½) 1 =½=0,5; Точка B.
x=2, y=(½) 2 =¼=0,25; Точка C.
x=3, y=(½) 3 =1/8=0,125; Точка D.
График функции у=2 х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.
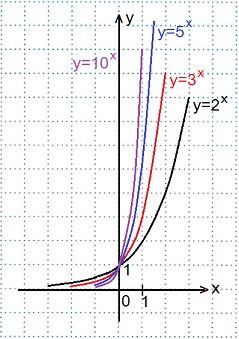
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
4) В одной координатной плоскости построить графики функций:
Смотрите построение графика функции y=( 1 /2) x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.
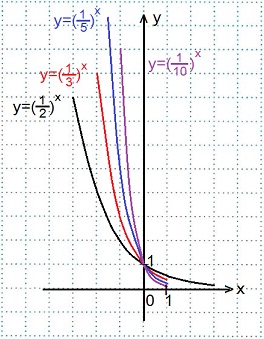
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Решить графически уравнения:
1) 3 x =4-x.
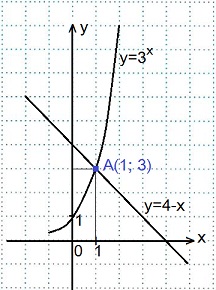
Графики пересеклись в точке А(1; 3).
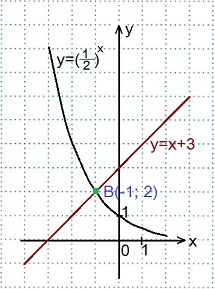
2) 0,5 х =х+3.
В одной координатной плоскости строим графики функций: у=0,5 х
Графики пересеклись в точке В(-1; 2).
1) y=-2 x
Область значений показательной функции y=2 x – все положительные числа, т.е.
0+ 1 1 /3) x + 1 1 ;
Запишем функцию в виде: у=3 х ∙3-5.
0∙ 3 x ∙ 3 3 ;
Что такое показатель функции
Ключевые слова: область определения функции, область значений функции четная функция, нечетная функция, периодическая функция. монотонная функция. убывающая функция. возрастающая функция, ограниченная функция.
В элементарной математике изучаются функции только на множестве действительных чисел R.
Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена,
т.e.она также принимает только действительные значения.
Множество X всех допустимых действительных значений аргументаx, при которых функция y = f (x) определена, называется областью определения функции.
Множество Y всех действительных значений y, которые принимает функция,называется областью значений функции.
Теперь можно дать более точное определение функции:
правило(закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.
 |  |
Функция считается заданной, если:
Если для любых двух значений аргумента x1и x2 из условия x2 > x1 следует f ( x2 ) > f ( x1 ), то функция f (x ) называется возрастающей;
если для любых x1 и x2 из условия x2 > x1 следует f (x2)