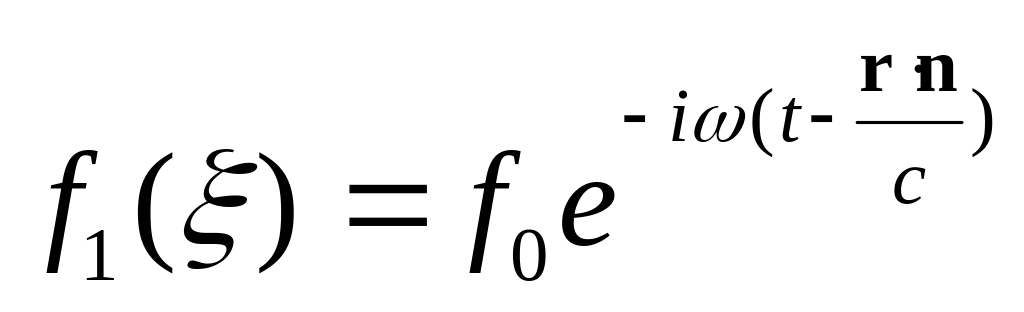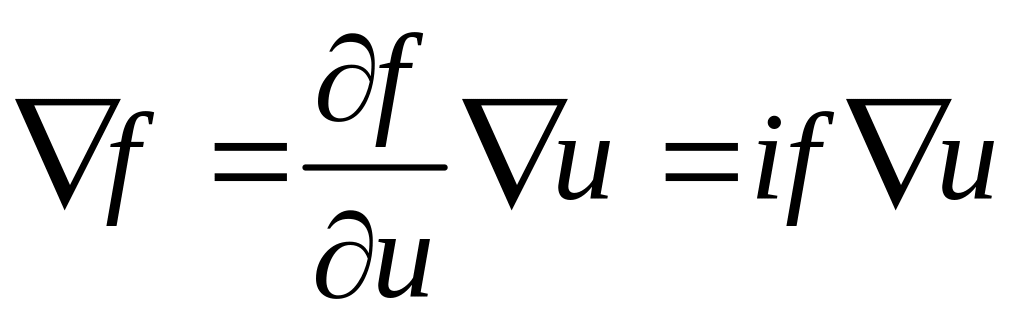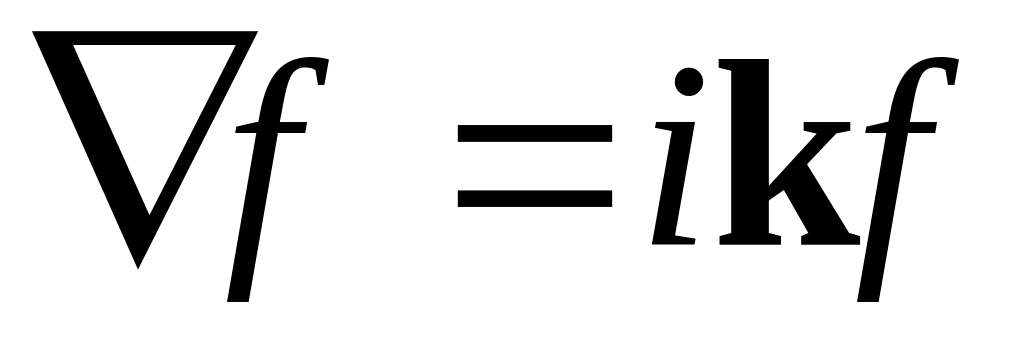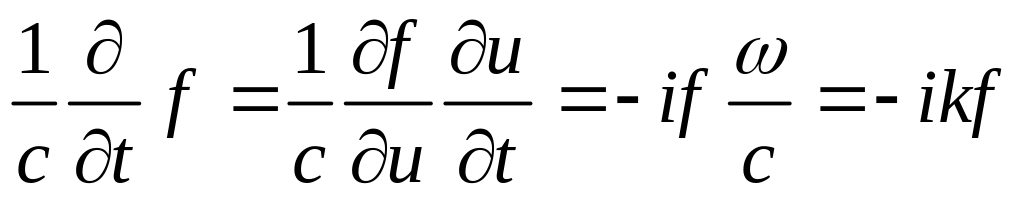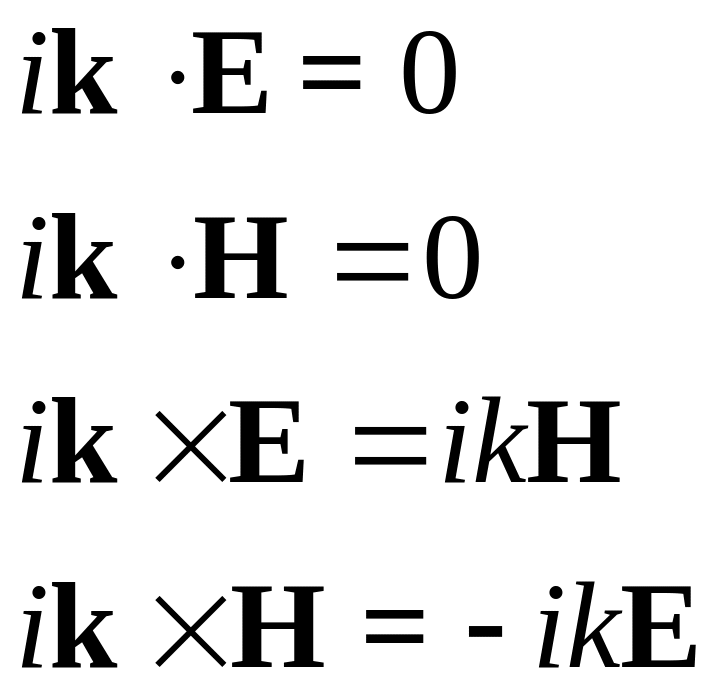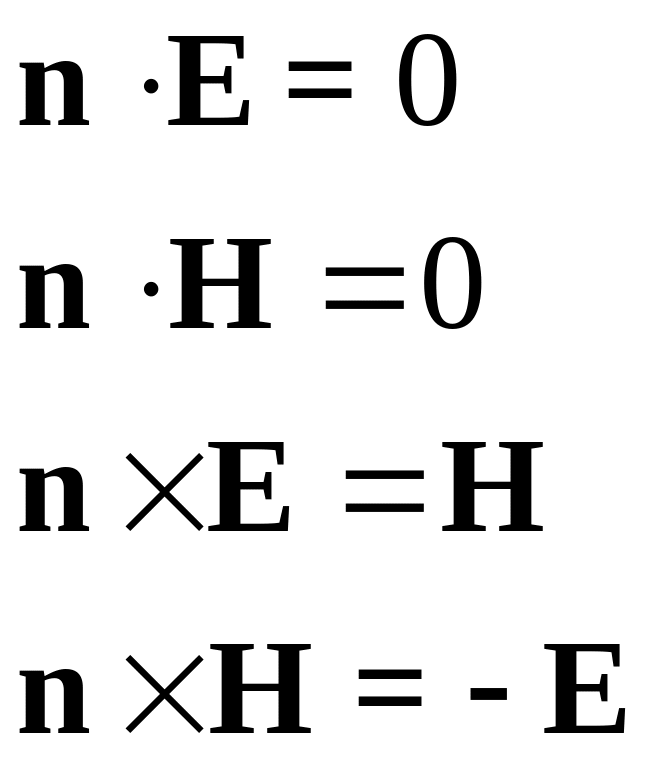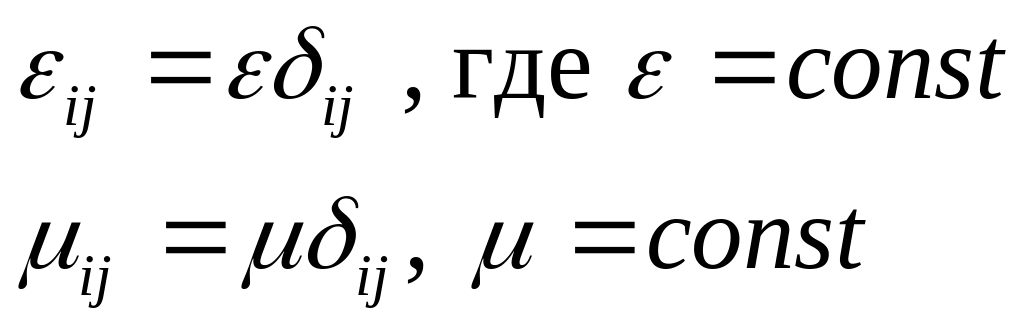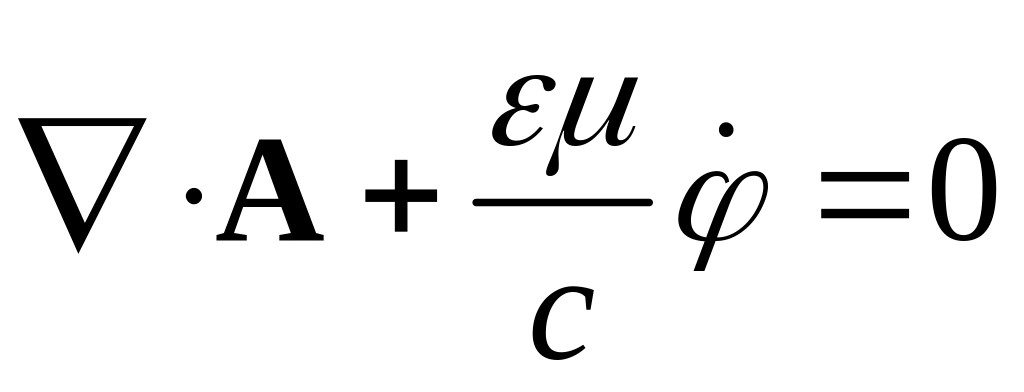что такое плоская монохроматическая волна

СОДЕРЖАНИЕ

Определение решения

Метрический тензор единственного точного решения, моделирующего линейно поляризованную плоскую электромагнитную волну с амплитудой q и частотой ω, можно записать в координатах Розена в виде

Для определения электромагнитного поля мы можем взять электромагнитный четырехвекторный потенциал

Теперь у нас есть полное описание математической модели, сформулированной в общей теории относительности.

Локальные изометрии

ξ → 1 знак равно ∂ v <\ displaystyle <\ vec <\ xi>> _ <1>= \ partial _ >

три пространственноподобных векторных поля,

и два дополнительных векторных поля,

Семья инерциальных наблюдателей

∇ е → 0 е → 0 знак равно 0 <\ displaystyle \ nabla _ <<\ vec > _ <0>> <\ vec > _ <0>= 0>

∇ е → 0 е → 1 знак равно ∇ е → 0 е → 2 знак равно ∇ е → 0 е → 3 знак равно 0 <\ displaystyle \ nabla _ <<\ vec > _ <0>> <\ vec > _ <1>= \ nabla _ <<\ vec > _ <0>> <\ vec > _ <2>= \ nabla _ <<\ vec > _ <0>> <\ vec > _ <3>= 0>

Электромагнитное поле

Что касается нашей системы отсчета, электромагнитное поле, полученное из потенциала, указанного выше, равно

В нашей системе отсчета тензор энергии-импульса оказывается равным

Т j ^ k ^ знак равно q 2 грех 2 ⁡ ( ω ты ) 4 π [ 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 ] <\ displaystyle T ^ <<\ hat > <\ hat >> = <\ frac \ sin ^ <2>(\ omega u)> <4 \ pi>> < \ begin 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \ end >>

Относительное движение наблюдателей

Ненулевые компоненты идентичны и являются

Кривизна четко разделяется на волну (кривизна в разрезе, параллельная направлению распространения) и фон (кривизна в поперечном разрезе).

Тензор кривизны Римана

Оптические эффекты

Это показывает, что, глядя через уходящие волновые фронты на далекие объекты, наши инерциальные невращающиеся наблюдатели будут видеть изменение их видимого размера точно так же, как расширение самого времениподобного геодезического сравнения.

График Бринкмана

Это приводит решение к его представлению в терминах координат Бринкмана :

Каустики

В диаграмме Бринкмана наше поле кадра становится довольно сложным:

и так далее. Естественно, если мы вычислим тензор разложения, тензор электрогравитации и т. Д., Мы получим точно такие же ответы, как и раньше, но выраженные в новых координатах.

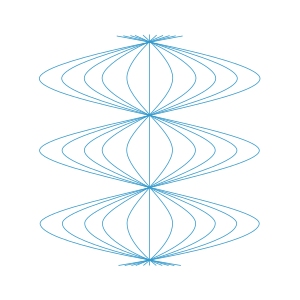
Поражает простота метрического тензора по сравнению со сложностью фрейма. Дело в том, что нам легче визуализировать каустику, образованную относительным движением наших наблюдателей на новой карте. Интегральные кривые единичного времениподобного геодезического векторного поля дают мировые линии наших наблюдателей. На диаграмме Розена они отображаются в виде вертикальных координатных линий, поскольку эта диаграмма движется вместе. Икс → знак равно е → 0 <\ displaystyle <\ vec > = <\ vec > _ <0>>

Чтобы понять, как эта ситуация проявляется в карте Бринкмана, обратите внимание, что, когда ω велико, наше времяподобное геодезическое единичное векторное поле становится приблизительно

Подавляя последний член, имеем

Мы сразу получаем интегральную кривую, которая демонстрирует циклы синусоидального расширения и обратного схождения. Посмотрите на рисунок, на котором время течет вертикально, и мы используем радиальную симметрию, чтобы подавить одно пространственное измерение. На этом рисунке показано, почему на диаграмме Розена имеется координатная сингулярность; наблюдатели должны фактически проходить мимо друг друга через равные промежутки времени, что явно несовместимо с сопутствующим свойством, поэтому диаграмма в этих местах ломается. Обратите внимание, что этот рисунок неверно предполагает, что один наблюдатель является как бы «центром притяжения», но на самом деле все они полностью эквивалентны из-за большой группы симметрии этого пространства-времени. Отметим также, что относительное движение наших наблюдателей в широком смысле синусоидальное полностью согласуется с поведением тензора расширения (относительно поля кадра, соответствующего нашему семейству наблюдателей), которое было отмечено выше.

Стоит отметить, что эти несколько хитрые моменты сбивали с толку не меньшую фигуру, чем Альберт Эйнштейн в его статье 1937 года о гравитационных волнах (написанной задолго до того, как современный математический аппарат, используемый здесь, получил широкое признание в физике).

Резюме

Источник

Монохроматическая плоская волна

Монохроматическая плоская волна

Векторный потенциал такой волны удобнее всего написать в виде вещественной части Людмила Фирмаль

Волна монохроматична, то ее поле является простой периодической функцией от т — х / с комплексного выражения: А = Re <А0е — «(*« х / с)>. (48.2) Здесь Ао-некоторый постоянный комплексный вектор. видно, что и напряженность (48.3) поляризованные координаты

Если аргумент этого числа есть —2а (т. е. уравнение = | Ед | е_2га), то вектор Ь, определенный согласно Е 0 = он, (48,7) будет иметь вещественный квадрат Ь2 = | Ео | 2-С таким опреде лением напишем Е = Re <Ье ^ (кг «ш *« а)>. (48,8) Представим б в виде b = bi + гЬ2, В квадрате Ь2 = = b \ — + 2гЪ \ Ъ2 должен быть вещественной величиной, то b ib 2 = 0, т. е. используются би и взаимно перпендикулярны. тогда из (48,8м) Еу = Ъ \ cos (вырезать-кр + се), Ez = = Ь & 2 sin (сот-кр + а), (48,9)

мы видим ства вектор электрического поля вращается в плоскости Людмила Фирмаль

Еру соответственно, правая и левая поляризация). Наконец-то, если Ь \ или 62 равно нулю Лено везде и всегда рядом (или антипараллельно) одному В этом случае линейно поляризованной или поляризованний поляризованную волну можно рассматривать, очевидно, как наложение двух линейно поляризованных вол Вернемся к определению рехмерный волновой вектор # = (^, к). (48.12) 4-вектор, очевидно, что при умножении на 4 волны он дает скаляр-фазу волны: kiXг = сот-кр. (48.13)

Из определений (48.4) и (48.12) видно, что квадрат волнового к% = 0. (48.14) Это выражение должно А = Ао exp (—ik (Xг) должно быть решение волнового уравнения (46.10). Как у всякой плоской волны, в монохроматической волне, распространенные по всей стране, только следующие компоненты тензора энергии-импум. rj-100 _ rj

Наконец, используя закон преобразования волнового 4-векто можно легко рассмотреть так называемый эффект Доплера-изменение частоты волны, испускаемостьии по отношению к наблюдателю, по сравнению с «собственной» частной речью Пусть V-скорость источника, т. Е. Скорость системы отсче та К 0 относительно К.

Задачи 1. Определить направление и значение осей эллипса поляризации по комплексной амплитуде Ео- B = bi + с вещественным квадратом. Из (48.7) имеем EoES = bj + bl, [EoEq] = —2г [bib2], (1) ИЛИ b \ + b \ = A2 + B2, bi b2 = AB sin

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Монохроматическая волна

Монохроматическая волна — модель в физике, удобная для теоретического описания явлений волновой природы, означающая, что в спектр волны входит всего одна составляющая по частоте.

Содержание

Основные свойства

Монохроматическая волна — строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой.

Бегущая монохроматическая волна

Вектор Умова-Пойнтинга S= [ExH] — вектор, направление которого совпадает с направлением распространения энергии в электромагнитной волне, а модуль |S| равен потоку энергии.

Стоячая монохроматическая волна

Стоячая монохроматическая волна — волна, формирующаяся при распространении двух плоских монохроматических электромагнитных волн одинаковой поляризации навстречу друг другу.

В природе и технике

В природе и технике наиболее близко к монохроматическому излучение отдельных линий спектров испускания свободных атомов и молекул. Эти линии соответствуют переходу атома из состояния с большей энергией в состояние с меньшей, а частоты соответствующих монохромных волн равны разнице уровней энергии, поделённой на постоянную Планка.

Связанные понятия

Когерентность

Две волны или несколько волн являются полностью когерентными, если частоты их одинаковы, амплитуды и разность фаз постоянны. Длина когерентности для таких волн равна бесконечности.

Плоскость поляризации — плоскость, задаваемая вектором напряжённости электрического поля E и вектором, указывающим направление распространения электромагнитной волны.

Примечания

Источники

Полезное

Смотреть что такое «Монохроматическая волна» в других словарях:

монохроматическая волна — monochromatinė banga statusas T sritis fizika atitikmenys: angl. monochromatic wave vok. monochromatische Welle, f rus. монохроматическая волна, f pranc. onde monochromatique, f … Fizikos terminų žodynas

Волна — У этого термина существуют и другие значения, см. Волна (значения). Волна изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами,… … Википедия

Гармоническая волна — Гармоническая волна согласно наиболее общему определению волна, каждая точка колеблющейся среды или поле в каждой точке пространства совершает гармонические колебания[1]. В разных случаях при необходимости особо выделяется… … Википедия

ПЛАЗМА — частично или полностью ионизованный газ, в котором плотности положит. и отрицат. зарядов практически одинаковы. При сильном нагревании любое в во испаряется, превращаясь в газ. Если увеличивать темп ру и дальше, резко усилится процесс термич.… … Физическая энциклопедия

Кольца Ньютона — Кольца Ньютона кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину. Содержание 1 Описание 2 … Википедия

Плазма — (от греч. plásma вылепленное, оформленное) частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь… … Большая советская энциклопедия

Поляризация волн — У этого термина существуют и другие значения, см. Поляризация. Поляризация волн характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны. В продольной… … Википедия

С-300 — У этого термина существуют и другие значения, см. С 300 (значения). ЗРС С 300 Пусковые установки С 300 на параде Победы в 2009 году … Википедия

Волновой пакет — распространяющееся волновое поле, занимающее в каждый момент времени ограниченную область пространства. В. п. может возникнуть у волн любой природы (звуковых, электромагнитных и т.п.). Такой волновой «всплеск» в некоторой области… … Большая советская энциклопедия

Поляризация электромагнитных волн — Поляризация для электромагнитных волн это явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H. Когерентное электромагнитное излучение может иметь: Эллипс поляризации Лине … Википедия

Источник

[§41.] Плоская монохроматическая волна.

Введём параметр 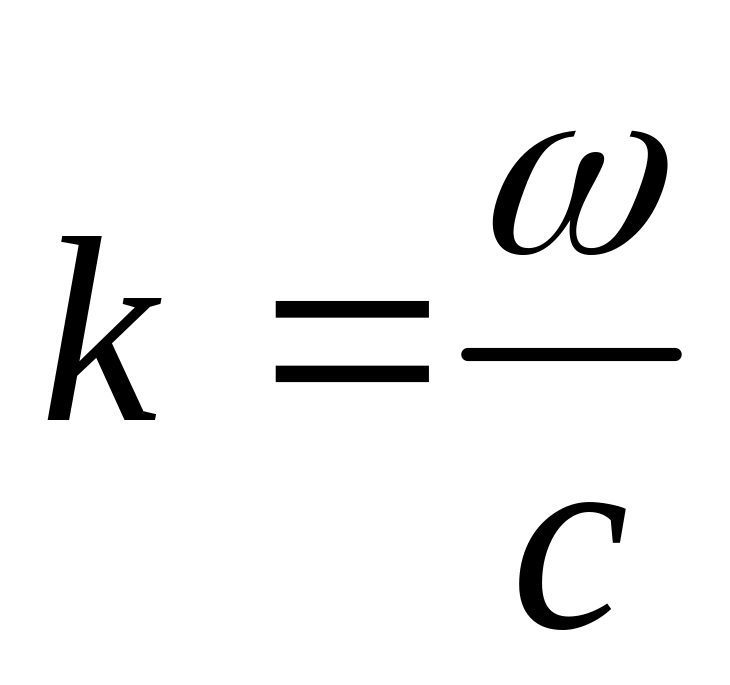— волновое число.

Введём волновой вектор 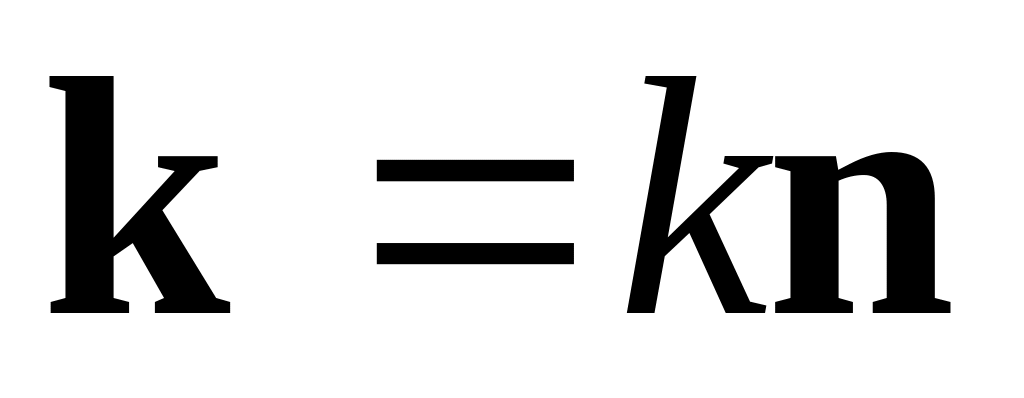, направленный по нормали к фронту волны. Тогда:

§42. Уравнения Максвелла в случае плоской монохроматической волны в вакууме.

Уравнения Максвелла в случае электромагнитных волн в вакууме имеют вид:

Т.к. поля и имеют зависимость

, то

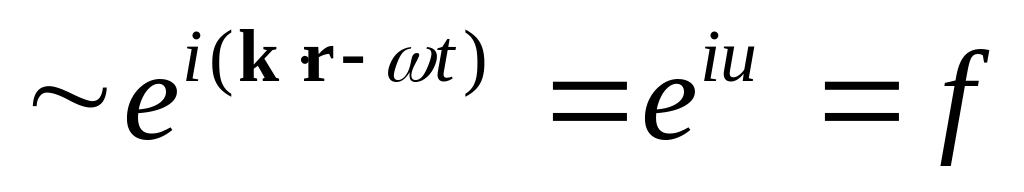
где 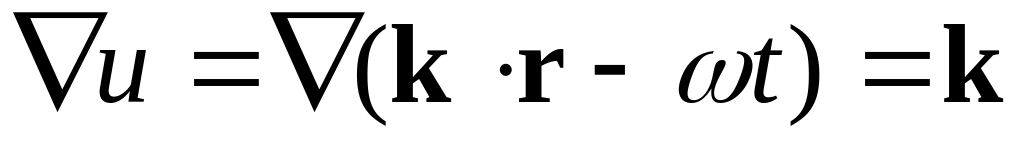, тогда:

В результате для плоских монохроматических волн операторы:

Тогда уравнения Максвелла для плоских монохроматических волн имеют вид:

§43. Разложение электромагнитных полей по плоским монохроматическим волнам.

Разложим :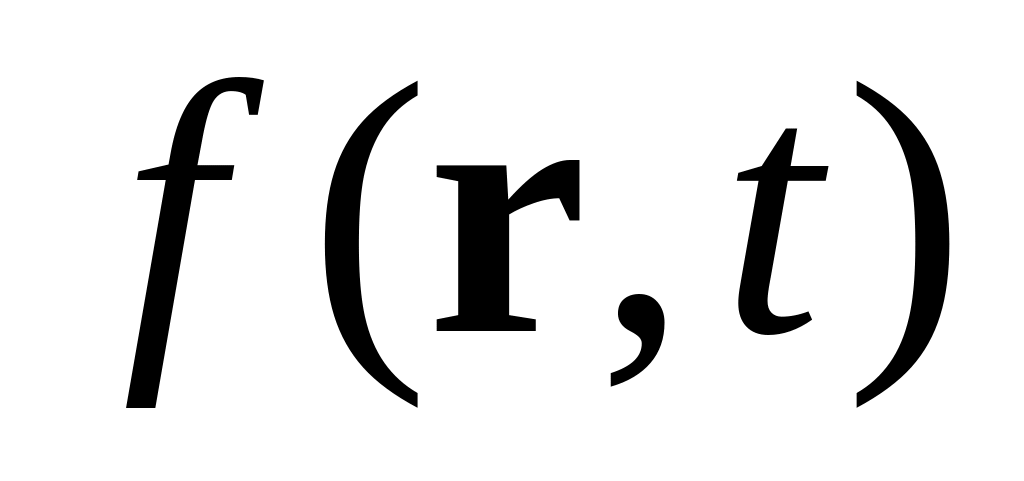

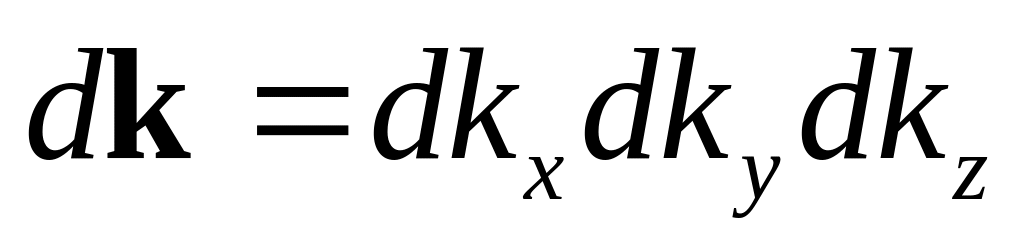
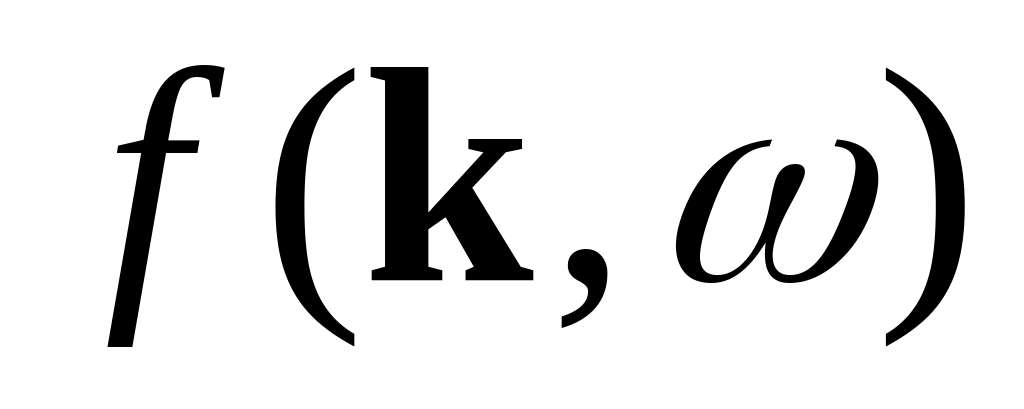
где , а — амплитуда данной монохроматической волны, присутствующей в электромагнитном поле, т.е. это вес волны.

§44. Калибровка Лоренца в случае однородной изотропной среды.

Калибровка Лоренца в случае вакуума:

В случае однородной изотропной среды калибровка Лоренца примет вид:

Задачи по курсу «Теоретическая механика и теория поля»

[ 1.] Наити функцию Лагранжа двойного плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g).

2 . Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m₂, точка которого (с массой m₁ в ней) может совершать движения по горизонтальной прямой.

[3.] Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.

[4.] Определить скобки Пуассона, составленные из декартовых компонент импульса р и момента импульса материальной частицы.

5. Определить скобки Пуассона, составленные из компонент М.

где φ – любая скалярная функция координат и импульса частицы.

где f – векторная функция координат и импульса частицы, а n – единичный вектор в направлении оси z.

8. Выразить амплитуду и начальную фазу колебаний через начальные значения x₀, v₀ координаты и скорости.

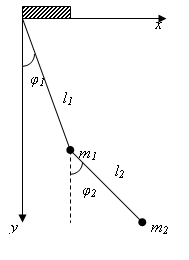
1 0. Найти частоту колебаний изображенного на рисунке 4 маятника, точка подвеса которого (с массой m₁ в ней) способна совершать движение в горизонтальном направлении.

1 1. Определить малые колебания двойного плоского маятника.

12. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.

13. Вычислить где p – постоянный вектор.

14. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:

если объем, который охватывает замкнутая поверхность, равен V; A – постоянный вектор.

15. В равномерно заряженном шаре с объемной плотностью заряда имеется шарообразная полость, центр которой расположен на расстоянии а от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно R и .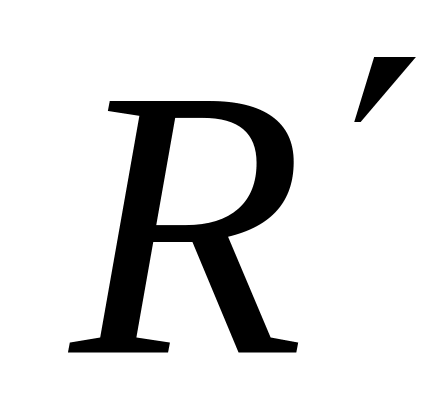

17. Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье.

18. Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону :

19. Определить потенциал точечного заряда е, находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости.

20. Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностью j. Оси цилиндра, образующего полость, и цилиндрического проводника параллельны и находятся друг от друга на расстоянии а.

Источник