что такое площадь поверхности прямоугольного параллелепипеда формула
Площадь поверхности прямоугольного параллелепипеда

Всего получено оценок: 386.
Всего получено оценок: 386.
В 5 классе в курсе математики изучается тема прямоугольного параллелепипеда. Сегодня мы поговорим о формулах для нахождения площади боковой поверхности и площади полной поверхности этой фигуры, которые наиболее часто вызывают затруднения у учеников.
Определения
Параллелепипед – это фигура в пространстве, которая состоит из шести четырехугольников.
Каждый четырехугольник – это грань параллелепипеда. Среди граней различают четыре боковые и два основания. Если в основании фигуры находится прямоугольник, то многогранник называется прямоугольным параллелепипедом.
Стороны граней – это ребра. У параллелепипеда всего 12 ребер.
Параллелепипед имеет 8 вершин, для их обозначения используют заглавные латинские буквы.
Если две грани не имеют общего ребра, то они называются противоположными. Так как каждая грань прямоугольного параллелепипеда – это прямоугольник, у которого противоположные стороны равны, то и противоположные грани прямоугольного параллелепипеда также равны.
Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.
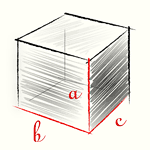
Примеры таких фигур мы часто встречаем в нашей жизни: кирпич, коробка, системный блок компьютера.
Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.
Различают несколько видов параллелепипедов, с основанием в виде квадрата, параллелограмма или прямоугольника.
Формула для нахождения площади
Для того, чтобы найти площадь боковой поверхности прямоугольного параллелепипеда, необходимо вычислить по отдельности площадь каждой боковой грани, а затем просуммировать получившиеся значения.
$S = ac$; где a, b, c – стороны фигуры.
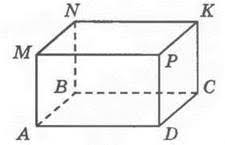
Соответственно, чтобы вычислить площадь полной поверхности прямоугольного параллелепипеда необходимо сложить площадь боковой поверхности и две площади основания. В итоге получится формула площади прямоугольного параллелепипеда.
$S = 2(ab + ac) + 2 bc = 2(ab + ac + bc)$
Иногда для уточнения возле знака площади пишут краткое обозначение например, S п.п. – площадь полной поверхности, либо S б.п. – площадь боковой поверхности. Это помогает во время выполнения задания не перепутать нужные данные.
Пример задания
Найти площадь полной поверхности прямоугольного параллелепипеда, если длина и ширина основания 4 см и 3 см соответственно, а высота равна 2 см.
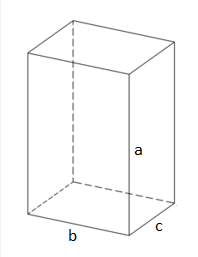
Решение:
S п.п. = 2(4*3 + 4*2 + 3*2) = 52 см 2
Для площади поверхности прямоугольного параллелепипеда используют те же единицы измерения, в которых были приведены длины ребер. Если длины ребер прямоугольного параллелепипеда даны в разных единицах измерения, то их нужно перевести в одинаковые.
Что мы узнали?
Мы познакомились с элементами прямоугольного параллелепипеда: грани, ребра, основание. А также ознакомились с формулами для нахождения площади его боковой и полной поверхности, которые можно использовать для решения заданий.
Как вычислить площадь параллелепипеда
Формула нахождения полной площади параллелепипеда
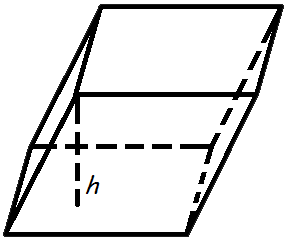
Параллелепипед – это четырехугольная призма, в основании имеющая параллелограмм. Существуют готовые формулы для расчета боковой и полной площади поверхности фигуры, для которых необходимы лишь длины трех измерений параллелепипеда.
Как найти площадь боковой поверхности прямоугольного параллелепипеда
Необходимо различать прямоугольный и прямой параллелепипед. Основание прямой фигуры может представлять собой любой параллелограмм. Площадь такой фигуры необходимо вычислять по другим формулам.
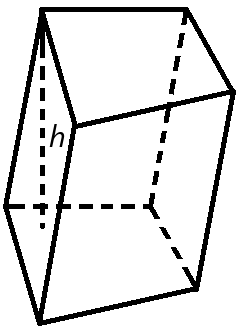
Сумма S боковых граней прямоугольного параллелепипеда вычисляется по простой формуле P*h, где P – периметр и h – высота. На рисунке видно, что у прямоугольного параллелепипеда противоположные грани равны, а высота h совпадает с длиной ребер, перпендикулярных основанию.
Площадь поверхности прямоугольного параллелепипеда
Полная площадь фигуры состоит из боковой и площади 2-х оснований. Как найти площади прямоугольного параллелепипеда:

, где a, b и c – это измерения геометрического тела.
Описанные формулы просты для понимания и полезны при решении множества задач геометрии. Пример типового задания представлен на следующем изображении.
При решении подобного рода задач следует помнить, что основание четырехугольной призмы выбирается произвольно. Если за основание принять грань с измерениями x и 3, то значения Sбок будет иным, а Sполн останется 94 см2.
Площадь поверхности куба
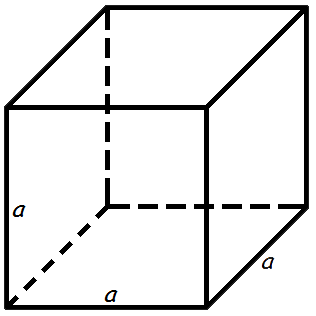
Куб – это прямоугольный параллелепипед, у которого все 3 измерения равны между собой. В связи с этим формулы полной и боковой площади куба отличаются от стандартных.
Периметр куба равен 4a, следовательно, Sбок= 4*a*a = 4*a2. Данные выражения не обязательны для заучивания, но значительно ускоряют решение заданий.
Пример решения задачи
Приведенные формулы могут использоваться в ходе поиска диагоналей параллелепипеда.
Для нахождение B1D достаточно применить теорему Пифагора: сумма квадратов катетов равна квадрату гипотенузы.
Онлайн калькулятор. Площадь прямоугольного параллелепипеда.
Используя этот онлайн калькулятор, вы сможете найти площадь поверхности прямоугольного параллелепипеда.
Воспользовавшись онлайн калькулятором для вычисления площади поверхности прямоугольного параллелепипеда, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь поверхности прямоугольного параллелепипеда
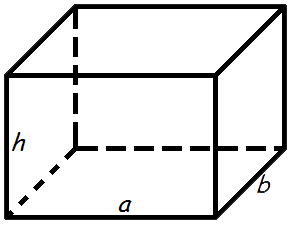
| a = |
| b = |
| h = |
Ввод данных в калькулятор для вычисления площади прямоугольного параллелепипеда
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади прямоугольного параллелепипеда
Теория. Площадь поверхности прямоугольного параллелепипеда
Формула для вычисления площади прямоугольного параллелепипеда
S = 2( a · b + a · h + b · h )
Площадь поверхности параллелепипеда
Вы будете перенаправлены на Автор24
На этой странице вы узнаете, как выглядят формулы для расчёта полной и боковой площади поверхности параллелепипеда. Также на страницу добавлен онлайн-калькулятор для расчёта площади прямоугольного параллелепипеда.
Параллелепипед является разновидностью призмы, основания которой представляют собой параллелограммы. Также параллелепипедами называют призмы, в основании которых лежат многогранники, а все грани являются параллелограммами.
Наиболее знакомый всем вид параллелепипеда — это прямоугольный параллелепипед. Все его грани являются прямоугольниками.
Для расчёта полной площади прямоугольного параллелепипеда введите значение сторон и высоты в поля для ввода.
Площадь поверхности параллелепипеда через стороны
Для прямоугольного параллелепипеда площадь поверхности определяется по формуле:
$S = 2 \cdot (a \cdot b + b \cdot h + a \cdot h)$, здесь
$a, b$ — стороны основания параллелепипеда;
$h$ — высота параллелепипеда.
Разберём пример на нахождение полной площади параллелепипеда.
Задача
Решение:
Воспользуемся вышеприведённой формулой:
$S = 2 \cdot (3 \cdot 4 + 7 \cdot 4 + 3 \cdot 7) = 122$ кв. см.
Результаты совпадают с решением онлайн-калькулятора, а значит, ответ найден верно.
Также используя следующий онлайн-калькулятор, вы сможете рассчитать площадь боковой поверхности прямоугольного параллелепипеда.
Площадь боковой поверхности прямоугольного параллелепипеда через стороны
Площадь боковой поверхности прямоугольного параллелепипеда определяется по формуле:
$S = 2 \cdot h \cdot (a + b)$, где
$h$ — длина ребра параллелепипеда;
$a, b$ — стороны основания.
Рассчитаем для примера площадь боковой поверхности для параллелепипеда из предыдущей задачи.
Задача
Решение:
$S_б = 2 \cdot 4 \cdot (3 + 7) = 80$ кв. см.
Решение соответствует решению, полученному с помощью онлайн-калькулятора, а значит, ответ правильный.
Что такое площадь поверхности прямоугольного параллелепипеда формула
Объем куба равен кубу длины его грани.
Формула объема куба
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды
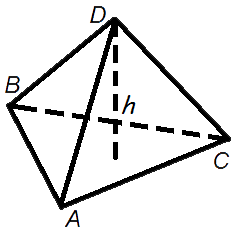
Объем правильного тетраэдра
Формула объема правильного тетраэдра
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса
Объем шара
Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи.
Формула объема шара
Площадь куба
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Формула площади куба
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра