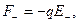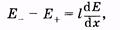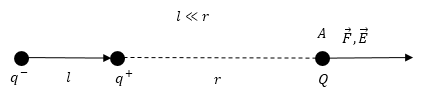что такое плечо диполя

Электрический диполь

Электрическим диполем (диполем) называют систему, состоящую из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга (плечо диполя).

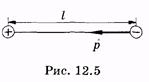
Основной характеристикой диполя (рис. 12.5) является его электрический момент (дипольный момент) — вектор, равный произведению заряда на плечо диполя l, направленный от отрицательного заряда к положительному:

(12.19)

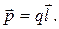
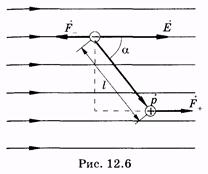Единицей электрического момента диполя является кулон-метр. Поместим диполь в однородное электрическое поле напряженностью 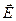(рис. 12.6).

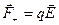
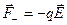
На каждый из зарядов диполя действуют силы и , эти силы равны по модулю, противоположно направлены и создают момент пары сил. Как видно из рисунка, он равен

М = qElsin a = pEsin a, (12.20) или в векторной форме 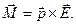. (12.21)

Таким образом, на диполь в однородном электрическом поле действует момент силы, зависящий от электрического момента и ориентации диполя, а также напряженности поля.

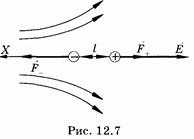
Рассмотрим теперь диполь в неоднородном электрическом поле. Предположим, что диполь расположен вдоль силовой линии (рис. 12.7). На него действуют силы

и

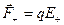
где Е₊ и Е_ — напряженности поля соответственно в месте нахождения положительного и отрицательного зарядов (на рис. 12.7 Е_— > Е₊). Значение равнодействующей этих сил

где dE/dx — производная от напряженности электрического поля по направлению оси ОХ, являющаяся мерой неоднородности электрического поля вдоль соответствующего направления. Из (12.23)следует, что

тогда формулу (12.22) можно представить в виде

(12.24)

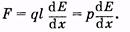
Итак, на диполь действует сила, зависящая от его электрического момента и степени неоднородности поля dE/dx. Если диполь ориентирован в неоднородном электрическом поле не вдоль силовой линии, то на него дополнительно действует еще и момент силы. Таким образом, свободный диполь ориентируется вдоль силовых линий и втягивается в область больших значений напряженности поля.

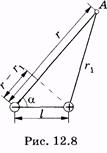
До сих пор рассматривался диполь, помещенный в электрическое по­ле, однако сам диполь также является источником поля. На основании (12.18) запишем выражение для электрического потенциала поля, со­зданного диполем, в некоторой точке А, удаленной от зарядов соответ­ственно на расстояния гиг, (рис. 12.8):

(12.25)

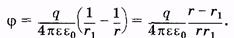
Обычно предполагают, что l

(12.28)

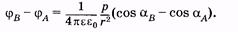
Учитывая эти равенства, выполним тригонометрические преобразования:

(12.29)

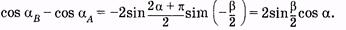
Подставляя (12.29) в (12.28), имеем

(12.30)

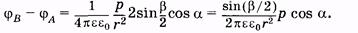
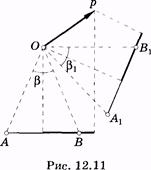
Как видно из (12.30), разность потенциалов двух точек поля диполя, равноотстоящих от него (при данных e и r), зависит от синуса половинного угла, под которым видны эти точки от диполя (рис. 12.10), и проекции электрического момента диполя р cos a на прямую, соединяющую эти точки (рис. 12.11). Эти замечания справедливы в рамках тех ограничений, которые были сделаны при выводе формулы (12.27).

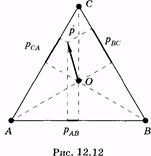
Пусть диполь, создающий электрическое поле, находится в центре равностороннего треугольника ABC (рис. 12.12). Тогда на основании (12.30) можно получить, что напряжения на сторонах этого треугольника относятся как проекции вектора 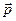на его стороны:

Источник

Электрический диполь

Вы будете перенаправлены на Автор24

Что такое электрический диполь

Электрическим диполем называется система из двух точечных зарядов, величина которых одинакова, но противоположна по знаку, при чем, эти точечные заряды разнесены на небольшое расстояние друг от друга. Вектор, соединяющий отрицательный заряд с положительным (направление от минуса к плюсу), называется плечом диполя.

Тогда векторная величина, равная:

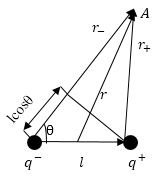
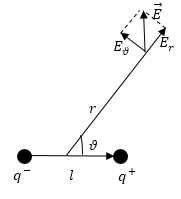
Электрическое поле диполя складывается из напряжённостей зарядов, которые составляют диполь. Так как плечо диполя мало, поэтому можно считать, что оно много меньше, чем расстояние до точек, в которых рассчитывается напряженность поля. Найдем потенциал диполя. В точке А (рис.1) формула для потенциала будет иметь вид:

При этом местоположение точки A можно характеризовать вектором$\overrightarrow<\ r>$ с началом в любой точке диполя, ввиду малых геометрических размеров диполя. В таком случае формулу (2) можно записать в виде:

запишем формулу для напряженности поля диполя, которая будет иметь вид:

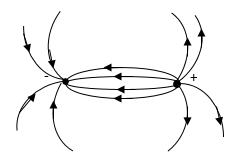
Согласно формуле (6) напряженность поля диполя убывает быстрее, чем напряженность кулоновского поля одиночного заряда, пропорционально третьей степени расстояния. Силовые линии электростатического поля около диполя изображены на рис. 2.

Модуль вектора сопряженности

В таком случае модуль вектора напряженности равен:

Вычисление момента сил

В однородном поле сила, которая действует на диполь со стороны поля ($\overrightarrow$), равна нулю, так как к зарядам приложены одинаковые по модулю и противоположные по направлению силы:

Момент этих сил равен:

Если поле не однородно, то сила (сумма сил действующих на положительный и отрицательный заряд) не равна нулю.$\ \overrightarrow=<\overrightarrow>_++<\overrightarrow>_-\ne 0$. В этом случае сила равна:

В том случае, если мы имеем дело с точечным диполем (плечо диполя очень мало), то сила, действующая на диполь, может быть записана как:

или, что то же самое, но короче:

Задание: Ответьте на вопрос: может ли точечный заряд двигаться с постоянной скоростью вокруг неподвижного точечного диполя?

Напряженность поля, которое создает диполь в точке А (где помещен заряд q) равна:

Тогда силу с которой поле диполя действует на заряд, который помещен в точку А найдем как:

\[F=Q\cdot E\ \left(2.3\right).\]

В результате получаем:

Источник

Что такое плечо диполя

Подобно электрическому диполю, магнитный диполь — это векторная величина, т.е. в нашем трехмерном пространстве диполь содержит три компоненты. В отличие от электрического диполя магнитный диполь нельзя представить пространственно-разделенными зарядами противоположного знака, так как не существует магнитных зарядов. Единица измерения магнитного момента следует из представления магнитного диполя витком с током, в СИ [m] = А·м$<>^<2>$.

Дипольным приближением можно пользоваться и в микроскопических масштабах (например, в случае атомных или молекулярных токов), и в лабораторных экспериментах с токовыми витками или постоянными магнитами, лишь бы расстояние до точки наблюдения было больше размеров диполей. Сейчас известно, что многие частицы, из которых состоит вещество: электроны, протоны, нейтроны, ядра атомов и многие ионы, ведут себя как магнитные диполи, т.е. обладают собственным магнитным моментом и создают магнитное поле, находясь даже в покое. Более детальное рассмотрение показывает, что магнитный момент этих частиц тоже можно представить круговым током, т.е. вращающимися электрическими зарядами. Постоянные магниты изготавливают из ферромагнитных материалов, в которых магнитные моменты молекулярных токов ориентированы параллельно друг другу и «заморожены» в этом состоянии.

Как и любая физическая система, магнитный диполь стремится перейти в положение с наименьшей потенциальной энергией и поэтому ориентируется в направлении внешнего магнитного поля. Благодаря вращательному моменту стрелка компаса поворачивается в направлении магнитного поля.

Принципы работы магнитных датчиков

Для усиления эффекта используют многовитковую катушку, а также вставляют внутрь стержень из ферромагнитного материала.

Датчик этого типа реагирует только на изменение магнитного потока, а следовательно, он не сможет измерять стационарные поля. Достоинством ИД является чрезвычайно широкий диапазон измеряемых магнитных полей, а также возможность создания датчиков слабых полей.

В работе применяются датчики, основанные на эффекте Холла. В простейшем случае эффект Холла состоит в том, что в проводнике, по которому течет ток, под действием внешнего магнитного поля возникает разность потенциалов между боковыми гранями:

Последнее упомянутое свойство позволило в 1879 г. Эдвину Холлу экспериментально доказать, что ток в металлах создается направленным движением именно электронов.

Теперь рассмотрим основные характеристики датчиков магнитного поля. Как определить, какой датчик лучше подходит для конкретной задачи? Основной характеристикой датчика является его чувствительность. Обычно чувствительность указывают в В/Тл, т.е. если чувствительность равна 1 В/Тл, то в поле 1 тесла на датчике возникнет напряжение 1 вольт. Например, среднее магнитное поле Земли составляет 50 мкТл и датчик с чувствительностью 1 В/Тл не очень подходит для его измерения.

Другой важной характеристикой датчика является диапазон измеримых полей. Обычно под этим подразумевают максимальное значение поля, которое можно измерить датчиком. Многие типы датчиков имеют свойство «насыщаться», т. е. при приложении поля, большего чем максимальное, датчик выдает одно и то же значение напряжения, вне зависимости от поля.

Для некоторых видов датчиков указывают температурные коэффициенты, например, дрейф магнитной чувствительности (magnetic sensitivity temperature drift). Обычно в процентах. Этот коэффициент показывает, на сколько процентов изменяется чувствительность при изменении температуры на 1 градус. Зависимость магнитной чувствительности от температуры связана, прежде всего, с изменением сопротивления элементов датчика при изменении температуры.

Современные датчики обычно содержат в себе встроенные усилители, поэтому в документации к датчикам приводятся параметры, характерные для усилителей, например, смещение нуля. Смещение нуля означает, что при нулевом магнитном поле на выходе датчика будет соответствующее ненулевое напряжение.

Назад к описанию лабораторных работ раздела Электростатика и магнитостатика или далее к описанию эксперимента

Источник

1.3. Основные характеристики электрического поля. Электрический диполь. Поле диполя. Диполь в электрическом поле.

Электрическим диполем (диполем) называют систему, состоящую из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга (плечо диполя).

Основной характеристикой диполя (рис.4) является его электрический, или дипольный момент – вектор, направленный от отрицательного заряда к положительному и равный произведению заряда на плечо диполя:

Единицей электрического момента диполя является кулон-метр.

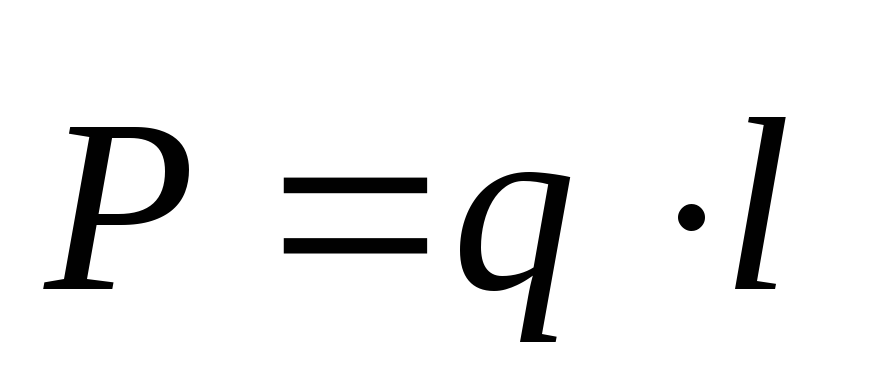
Поместим диполь в однородное электрическое поле напряжённостью (рис.5). На каждый из зарядов диполя действуют силы=qи

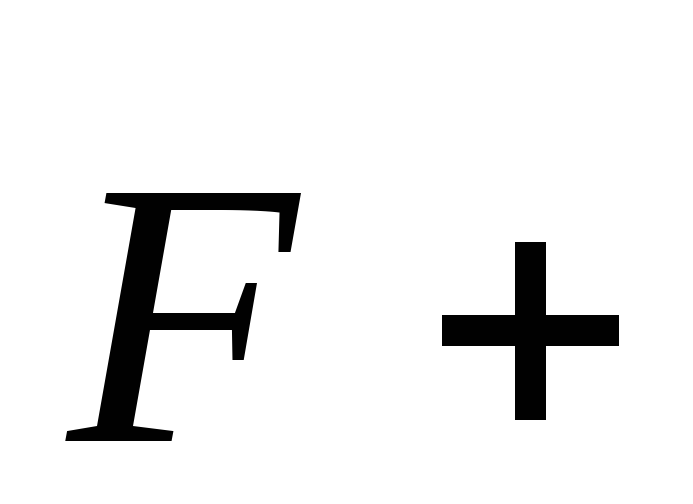
Или в векторной форме

=(10)

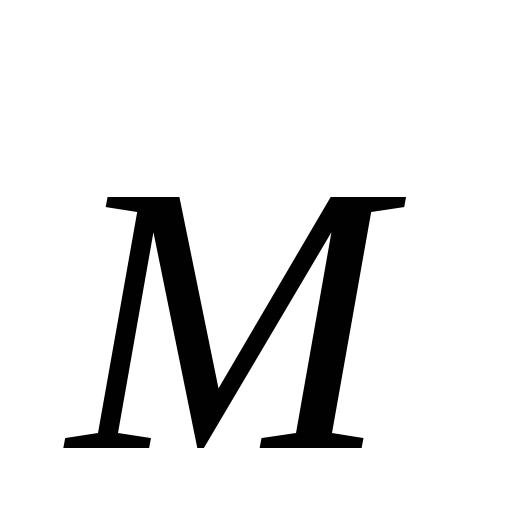
Таким образом, на диполь в однородном электрическом поле действует вращающий момент, зависящий от электрического момента, ориентации диполя в поле и напряжённости поля.

Рассмотрим теперь диполь в неоднородном электрическом поле. Простоты ради предположим, что диполь расположен вдоль силовой линии. На него действуют силы

где dE/dx – производная от напряженности электрического поля по направлению оси ОХ, являющаяся мерой неоднородности электрического поля вдоль соответствующего направления. Из (12) следует

Тогда формулу (5) можно представить в виде

F = ql dE/dx = p dE/dx.

Итак, на диполь действует сила, зависящая от его электрического момента и степени неоднородности поля dE/dx.

Если диполь ориентирован в неоднородном электрическом поле не вдоль силовой линии, то на него дополнительно действует еще и вращающий момент. Так что свободный диполь практически всегда будет втягиваться в область больших значений напряженности поля.

1.4. Дипольный эквивалентный электрический генератор сердца.

В возбужденном миокарде всегда имеются много диполей (назовем их элементарными). Потенциал поля каждого диполя в неограниченной среде подчиняется уравнению:

, где (13)

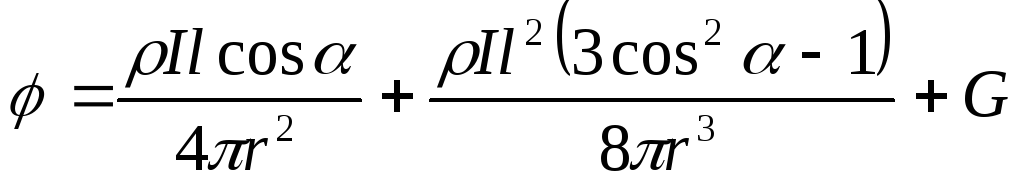
При изучении потенциалов на значительном удалении от сердца, когда выполняется условие rl, первый член правой части уравнения (13) намного превосходит остальные. Поэтому в первом приближении вторым и последующими членами можно пренебречь. Это заведомо справедливо в случае точечных диполей, у которых l0. Первый член в правой части уравнения (13) именуют дипольным потенциалом (потенциалом точечного диполя).

Потенциал (₀) электрического поля сердца складывается из дипольных потенциалов элементарных диполей. Поскольку в каждый момент кардиоцикла возбуждается сравнительно небольшой участок миокарда, расстояния от всех диполей до точки измерения потенциала примерно равны друг другу, и ₀ приближенно описывается уравнением:

, (14)

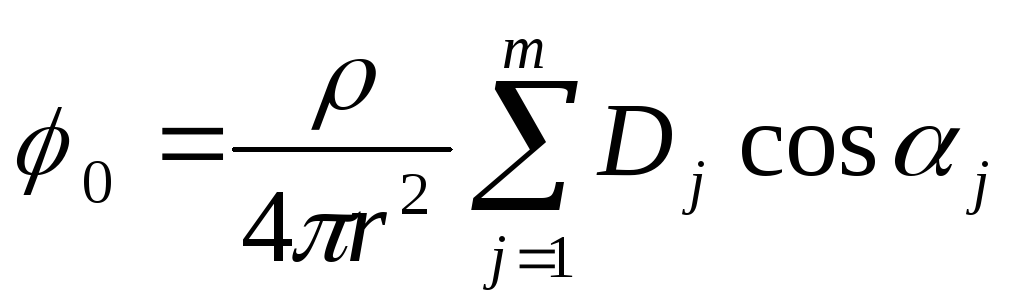
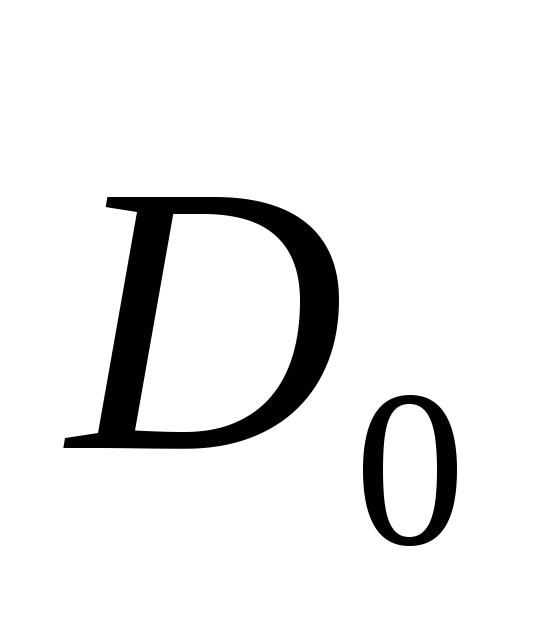
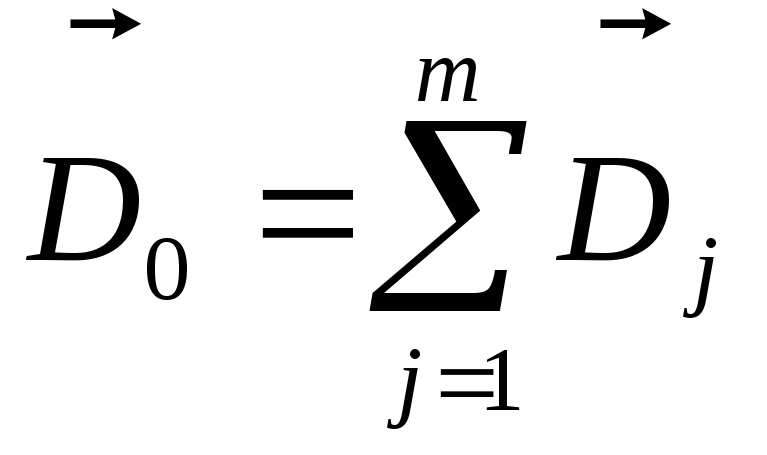
в котором r – одинаковое для всех диполей расстояние до точки измерения потенциала, m – количество диполей. Сумму проекций в этом выражении можно рассматривать как проекцию вектора дипольного момента () одного токового диполя, у которого

. (15)

Этот диполь называют эквивалентным диполем сердца. Таким образом, потенциал внешнего электрического поля сердца можно представить в виде дипольного потенциала одного эквивалентного диполя:

, (16)

Модель, в которой электрическая активность миокарда заменяется действием одного точечного диполя и потенциалы внешнего поля описываются выражением (11) называют дипольным эквивалентным электрическим генератором сердца.

Источник