что такое переходная кривая железнодорожного пути

Переходная кривая

Переходная кривая — кривая переменной кривизны, сопрягающая круговую кривую с прямым участком железнодорожного пути. Переходная кривая обеспечивает постепенное изменение центробежной силы при входе поезда в криволинейный участок пути. В пределах переходной кривой линейно возрастает необходимое в круговой кривой возвышение наружного рельса. Переменный радиус переходной кривой ρ плавно изменяется от ρ = ∞ в точках HK и KK сопряжения с прямой до ρ = R в точках КПК₁ и КПК₂ сопряжения переходной кривой с кривой радиуса R. Разбивка переходной кривой производится по радиоидальной спирали, кривизна которой изменяется пропорционально её длине.

Элементы переходной кривой (m, Т_ρ и другие) для облегчения их полевой разбивки приводятся в специальных таблицах. В практических расчётах приближённо считают, что переходная кривая очерчена по кубической параболе.

Длина переходной кривой при проектировании железной дороги принимается в соответствии со Строительными нормами и правилами в зависимости от радиуса круговой кривой и скоростей движения поездов. При проектировании реконструкции существующих железных дорог и строительства вторых путей часто возникает необходимость удлинения переходной кривой.

Источник

Круговые и переходные кривые.

Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).

Рис. 15.3 Схема круговой кривой

Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:

Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):

Домер вычисляют по формуле

. (15.2)

Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.

В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:

Правильность вычислений контролируют по формулам:

Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.

По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.

Вычислим пикетажное положение главных точек:

ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00

ПК НК 5 + 39,27 7 + 32,73

ПК КК 7 + 31,08 ПК КК 7 + 31,08

ПК НК 5 + 39,27 ПК ВУ 6 + 36,00

ПК СК 6 + 35,17 ПК СК 6 + 35,18

Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой . Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим

,

R – радиус кривизны в конце переходной кривой.

Индексом k отмечены значения переменных в конце переходной кривой.

Для радиуса кривизны переходной кривой в текущей точке i найдём:

где через l обозначена длина переходной кривой s_k. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.

Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол

.

Подставляя выражение радиуса кривизны r из (15.5), получим

.

Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:

,

Рис. 15.4 Схема переходной кривой:

а – углы поворота трассы: φ – в текущей точке i, β – в конце

Из полученного уравнения вытекают формулы:

; ; l = 2Rb, (15.6)

Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):

Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):

Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:

; (15.8)

. (15.9)

Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:

,

Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.

Рис. 15. 5 Смещение начала переходной кривой

Рис. 15.6 Сопряжение круговой кривой

Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q₁ и имеющая длину K = Ra.

При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна

Тангенс и биссектриса определяются по формулам:

Домер в этом случае равен

.

В полевых условиях значения m, Т_p и Б_p вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).

Источник

Переходная кривая

Перехо́дная крива́я (ПК) — элемент плана дороги, которым сопрягаются путевые прямые с круговыми кривыми и круговые кривые между собой.

Содержание

Предназначение

Переходная кривая используется для того, чтобы кривизна трассы изменялась плавно, а не скачкообразно в месте сопряжения элементов пути с разной кривизной (прямая и круговая кривая, круговые кривые разных радиусов или направленные в разные стороны в виде буквы S (обратные кривые)). При резком изменении кривизны пути поперечные силы, действующие на транспортное средство, изменяются скачкообразно, что приводит к повышенному динамическому воздействию на дорогу (путь) и экипажную часть, увеличивая их износ, повышает вероятность вылета за пределы дороги (схода с рельсов) или опрокидывания транспортного средства и вызывает дискомфорт у пассажиров.

Особенно важно устройство переходных кривых при высоких скоростях движения, применении путевых кривых малого радиуса, тяжёлом подвижном составе, пропуске длиннобазового подвижного состава (особенно ПС с длинной жёсткой базой, например паровозов).

Расчёт переходной кривой

Переходную кривую рассчитывают таким образом, чтобы в своём начале она имела кривизну, равную нулю (как у прямой, то есть начало кривой является точкой перегиба), а потом плавно меняла кривизну, в конце достигая значения, обратного радиусу круговой кривой (и наоборот для схода с виража). Поскольку переходная кривая является частью виража, на ней обеспечивается нарастающий поперечный уклон дорожного полотна (подъём внешнего рельса на рельсовых дорогах) до уровня, равного уклону на круговой кривой (и наоборот для схода с виража).

В качестве переходных чаще всего применяют следующие кривые:

Источник

Что такое переходная кривая железнодорожного пути

Между 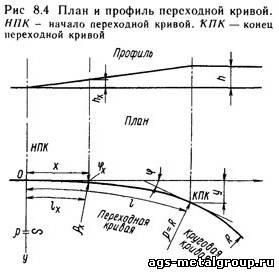прямыми и кривыми участками пути устраивают переходные кривые. Их назначение состоит в том, чтобы обеспечить плавный постепенный переход от прямой к кривой, не допускающий возникновения внезапных сил. Переходные кривые нужны, кроме того, еще и для плавного отвода возвышения наружного рельса и уширения колеи. Чтобы выполнить эти основные назначения, переходная кривая должна обладать рядом свойств.

В начале переходной кривой ее радиус должен быть бесконечно большим, чтобы это начало сливалось с прямой. В конце переходной кривой ее радиус должен быть равен радиусу примыкающей круговой кривой. На всем протяжении переходной кривой ее радиус должен непрерывно изменяться и, следовательно, должна изменяться ее кривизна.

На протяжении переходной кривой осуществляется отвод ширины колеи и постепенный подъем наружной нити до величины возвышения наружного рельса в круговой кривой. По этой причине переходная кривая должна иметь пространственную кривизну (как в плане, так и в профиле). Практически же в профиле делают прямолинейный отвод.

Таким образом, для того чтобы движение экипажей по переходной кривой было плавным, с постепенным нарастанием центробежных сил и ускорений, очень важно выбрать форму переходной кривой и обеспечить ее сохранение при текущем содержании.

Если длина переходной кривой мала, то при большой скорости движения экипаж проскочит эту кривую за очень малый промежуток времени. Практически при этом силы настолько быстро возрастут, что будут мало отличаться от внезапных. Поэтому очень важно правильно выбрать длину переходной кривой, которая должна быть различной на участках с разной скоростью движения. Длина кривой зависит от принятого уклона отвода возвышения, скорости движения, допустимой величины нарастания горизонтальных ускорений¹, допустимой скорости подъема колеса по наружному рельсу² и т. д. Для скорости до 120 км/ч принимают уклон отвода 0,001.

Длина переходной кривой определяется как произведение числа 1000 на величину возвышения наружного рельса. Например, при возвышении 50 мм (0,05 м) длина переходной кривой будет 1000 х 0,05 = 50 м.

Для участков пути, где скорости движения достигают 160 км/ч, уклоны отвода возвышения наружного рельса принимают не круче 0,00067, или 1 мм на 1,5 м. Там, где реализуются скорости до 200 км/ч, рекомендован уклон 0,0005, или 1 мм на 2 м.

При сопряжении смежных кривых (направленных в одну или в разные стороны) устраивают прямые вставки между начальными точками переходных кривых (а если их нет, то между начальными точками круговых кривых) как можно большей длины (табл. 4.2).

Стрелы изгиба в пределах переходных кривых (исключая точки начала и конца переходной кривой) подсчитывают так: стрелу изгиба в круговой кривой умножают на расстояние от начала переходной кривой до той точки, в которой определяют стрелу изгиба, и результат делят на длину переходной кривой.

Проверка длины переходной кривой может быть сделана так. Уточняют и фиксируют на наружном рельсе сечения, в которых превышение одного рельса над другим равно нулю (начало переходной кривой) и равно полному возвышению наружного рельса над внутренним в круговой кривой (конец переходной кривой). Далее прикладывают мерную ленту к головке рельса и измеряют фактическую длину переходной кривой.

——————
¹ Допускается 0,4 м/с³.
² Допускается 38 мм/с.

Источник

13. Железнодорожные кривые

Время чтения: 2 минуты

13.1. Переходная кривая

Непосредственное сопряжение прямого участка пути с круговой кривой приводят к тому, что во время движения поезда в местах сопряжения внезапно возникает центробежная сила F (рис. 88), прямо пропорциональная квадрату скорости движения υ и обратно пропорциональная радиусу кривой R

Рис.88. Силы, действующие на состав на прямом (а) и кривом (б) участке железнодорожного пути

Резкое воздействие центробежной силы на подвижной состав и железнодорожный путь, особенно при большой скорости движения, может привести к аварийной ситуации. Чтобы это не произошло, для постепенного нарастания центробежной силы конечные точки круговых кривых сопрягают с прямыми при помощи так называемых переходных кривых, радиус которых меняется от бесконечности (в начале переходной кривой) до радиуса круговой кривой (в точке сопряжения с последней). Кроме этого, в пределах переходных кривых осуществляют отведение возвышения наружного рельса до отметки внутреннего. Возвышение наружного рельса рассчитывается для каждой кривой в зависимости от среднего веса состава и расчетной скорости движения.

На железных дорогах России переходные кривые строят по радиондальной спирали (клотоиде) с изменением кривизны по линейному закону

, где — переменный радиус кривизны спирали в метрах; с – постоянная величина в квадратных метрах, показывает темп развития радиуса кривизны; — текущая длина переходной кривой.

При длине переходной кривой радиус её кривизны ; при равной проектной длине переходной кривой , радиус кривизны спирали равен радиусу круговой кривой: .

Переходные кривые принимают стандартной длины от 20 до 200 м, кратные 20 м, в зависимости от радиуса круговой кривой и скорости движения поездов.

При вставке переходных кривых радиус круговой кривой уменьшается на величину сдвижки. Чтобы при сопряжении переходной и круговой кривых радиус последней не уменьшался, предусматривается смещение центра круговой кривой проектного радиуса внутрь по биссектрисе угла, образованного направлениями трассы.

Рис. 89. Схема круговой и переходной кривых

На схеме (рис. 89) показаны элементы переходной кривой: приращение тангенса m, приращение радиуса р, приращение кривой Тр и приращение биссектрисы Бр, которые вычисляют по формулам

,

,

,

.

При устройстве переходной кривой центр круговой кривой смещается на величину р, а точки начала и конца кривой на величину m.

6.2. Железнодорожная кривая, её элементы и главные точки

В соответствии с нормами проектирования железных дорог на закруглениях должны устраиваться железнодорожные кривые в виде сочетания круговой кривой с двумя переходными кривыми (см. рис. 89).

Железнодорожная кривая имеет 7 элементов и 6 главных точек.

1. ВУ – вершина угла.

2. НК – начало железнодорожной кривой.

3. КК – конец железнодорожной кривой.

4. СК – середина железнодорожной кривой.

5. КПК1 – конец переходной кривой первой.

6. НПК2 – начало переходной кривой второй.

Элементы железнодорожной кривой:

1. У – угол поворота кривой (рассчитывается).

2. R – радиус круговой кривой (выбирается).

3. – длина переходной кривой. Выбор её зависит от категории дороги и радиуса кривой.

4. Тс – тангенс железнодорожной кривой. Определяется по формуле

5. Кс – длина железнодорожной кривой

Кс = К + ,

,

,

где β – угол половины переходной кривой

,

.

6. Бс – биссектриса железнодорожной кривой

7. Дс – домер железнодорожной кривой

Для контроля домер рассчитывают по следующей формуле

6.3. Вычисление пикетажа главных точек железнодорожной кривой и разбивка кривой в главных точках на местности

Вычисление пикетажа главных точек железнодорожной кривой выполняется по тем же формулам, что и для круговой кривой.

При необходимости вычисляют пикетажное значение точек конца и начала переходных кривых по формулам

КПК1 = НК + и НПК2 = КК – .

Разбивка кривой в главных точках на местности производят также, как и для круговой кривой.

13.4. Вопросы для самоконтроля

1. Что такое переходная кривая? Как и для чего она устраивается?

2. Какие элементы у переходной кривой.

3. Чем железнодорожная кривая отличается от круговой кривой?

4. Какими элементами и главными точками характеризуется железнодорожная кривая?

5. Как определяются элементы железнодорожной кривой?

Источник