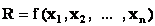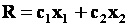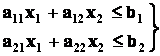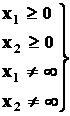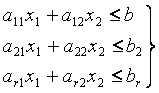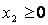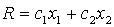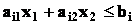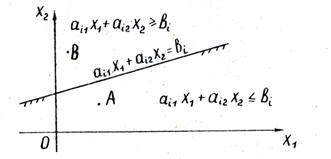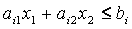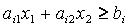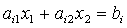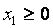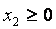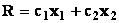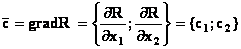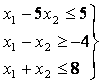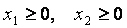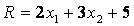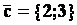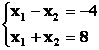что такое пассивная стратегия поиска при численном решении задач многомерной безусловной оптимизации
Лекция 2
Методы многомерной безусловной оптимизации. Прямые методы
Различные методы спуска отличаются выбором направления и величины шага.
Прямые методы или методы нулевого порядка не требуют знания целевой функции в явном виде. Они не требуют регулярности и непрерывности целевой функции и существования производных. Это является существенным достоинством при решении сложных технических и экономических задач. При реализации прямых методов существенно сокращается этап подготовки решения задачи, так как нет необходимости в определении первых и вторых производных. Прямые методы в основном носят эвристический характер. К прямым методам относится целый ряд алгоритмов, которые отличаются по своей эффективности. Методы предназначены для решения безусловных задач оптимизации
Алгоритм Гаусса
Метод очень прост, но не очень эффективен. Проблемы могут возникнуть, когда линии уровня сильно вытянуты и «эллипсоиды» ориентированы, например, вдоль прямых вида x 1 = x 2. В подобной ситуации поиск быстро застревает на дне такого оврага, а если начальное приближение оказывается на оси «эллипсоида», то процесс так и останется в этой точке.
Алгоритм Хука и Дживса
Если в процессе исследующего поиска не удается сделать ни одного удачного пробного шага, то необходимо скорректировать (уменьшить). После чего вновь переходим к исследующему поиску.
Если в процессе исследующего поиска сделан хоть один удачный пробный шаг, то переходим к поиску по образцу.
Из точки начинаем новый исследующий поиск и т.д.
Существуют модификации алгоритма, в которых в процессе исследующего поиска ищется минимум по каждой переменной или в процессе поиска по образцу ищется не минимум функции, а просто делается шаг в заданном найденном направлении с фиксированным значением параметра λ.
Алгоритм Розенброка
Критерии останова алгоритма могут быть стандартными (т.е. описанными в предыдущих алгоритмах прямых методов).
Симплексный метод Нелдера-Мида или поиск по деформируемому многограннику
где: ; ; t – расстояние между вершинами.
В самом простом виде симплексный алгоритм заключается в следующем. Строится регулярный симплекс. Из вершины, в которой максимальна (т.1) проводится проектирующая прямая через центр тяжести симплекса. Затем т.1 исключается и строится новый отраженный симплекс из оставшихся старых точек и одной новой, расположенной на проектирующей прямой на надлежащем расстоянии от центра тяжести.
Продолжение этой процедуры, в которой каждый раз исключается вершина, где целевая функция максимальна, а также использование правил уменьшения размера симплекса и предотвращение циклического движения в окрестности экстремума позволяет достаточно эффективно определять минимум для «хороших» функций. Но для «овражных» функций такой поиск неэффективен.
В симплексном алгоритме Нелдера и Мида минимизация функций n переменных осуществляется с использованием деформируемого многогранника.
В качестве критерия останова могут быть взяты те же критерии, что и в остальных алгоритмах. Можно также использовать критерий останова следующего вида:
Выбор коэффициентов α, β, γ обычно осуществляется эмпирически. После того как многогранник подходящим образом промасштабирован, его размеры должны поддерживаться неизменными пока изменения в топологии задачи не потребуют многогранника другой формы. Чаще всего выбирают α = 1, 0.4 ≤ β ≤ 0.6, 2 ≤ γ ≤ 3.
Методы безусловной оптимизации
Автор работы: Пользователь скрыл имя, 13 Июня 2013 в 14:58, реферат
Краткое описание
Задачи отыскания экстремумов в многомерном случае существенно осложняются. Возникают следующие качественно новые стороны рассматриваемой задачи:
Функция F(X) может иметь сложную форму. Для графической интерпретации поверхности принято изображать ее с помощью линий уровня. Линия уровня – это кривая в 2-х мерном сечении пространства параметров, значение функции, на которой константа. Поверхность, соответствующая зависимости F(X) может иметь: «овраги» или «гребни» (поверхности уровня имеют структуру, сильно отличающуюся от сферической); «плато» (плоские горизонтальные участки); особые точки типа «седло». Это не имеет себе аналогий в классе одномерных функций. («Седло» – точка гладкой поверхности, вблизи которой поверхность лежит по разные стороны от своей касательной плоскости. В окрестности седла имеются 4 интегральные кривые, которые входят в особую точку. Между ними располагаются интегральные кривые типа гипербол).
Вложенные файлы: 1 файл
Задачи отыскания экстремумов в многомерном случае существенно ос.doc
Г.И.Шкатова, Методы оптимизации
Методы безусловной оптимизации
Особенности поиска экстремума функции многих переменных
Задачи отыскания экстремумов в многомерном случае существенно осложняются. Возникают следующие качественно новые стороны рассматриваемой задачи:
Стратегия методов безусловной оптимизации
Все методы решения задач математического программирования можно разбить на прямые и непрямые. Непрямые методы основаны на использовании необходимых и достаточных условий экстремумов и сводятся к решению системы нелинейных уравнений
Методы, не связанные с использованием необходимых и достаточных условий экстремумов относят к прямым.
Большинство применяемых на практике прямых методов решения задач математического программирования являются итеративными.
В основу этих методов положен механизм порождения последовательности точек по правилам, которые определены в соответствии с выбранным методом решения и обладают следующими свойствами:
Общее правило построения последовательности численными методами безусловной оптимизации записывается в виде:
Стратегия предполагает на очередной итерации следующие шаги:
Выбор начальной точки производится, исходя из физического содержания решаемой задачи и наличия априорной информации о положении точек экстремума.
Выбор направления и величины шага определяется выбранным методом решения. Проверка критерия окончания итерационного процесса дает информацию о том, что либо решение задачи надо продолжить, либо найдена точка, претендующая на роль экстремума и процедуру поиска следует завешить.
Критерии для завершения поиска
На основании сравнения результатов расчетов двух или нескольких последовательных итераций. Наиболее распространены:
(1) – недостаточна, т.к. функция может иметь поведение типа скачка (резкое изменение критерия оптимальности).
(3) – характеризует скорость убывания критерия оптимальности и обращается в нуль в точке локального минимума. Поэтому по этой скорости можно судить о приближении к оптимуму.
Оценка эффективности методов оптимизации
Большое разнообразие итерационных алгоритмов ставит перед пользователем задачу выбора. Для этого следует выставить критерии, на основании которых один алгоритм будет считаться более предпочтительным, нежели другой. С этой целью обычно используют следующие оценки:
Для сравнения алгоритмов по этим критериям следует производить расчеты в одинаковых или близких условиях.
Классификация методов на основании порядка производных при выборе направления
Классификация методов на основании выбора метода аппроксимации целевой функции
Методы нулевого порядка
Представляет собой группу методов, у которых величина шага и направление к оптимуму формируются однозначно в зависимости от свойств критерия оптимальности в окрестности текущей точки без использования производных. Методы различаются выбором направления, начальных условий (начальной точки).
В методах покоординатного спуска осуществляется поиск из заданной точки в направлении, параллельном одной из осей, до точки минимума в данном направлении.
Затем поиск производится в направлении, параллельном другой оси и т.д.
Направления, конечно, фиксированы. Все многообразие этой группы методов определяется стратегией выбора очередной оси поиска и методом поиска (любым из методов одномерной минимизации) экстремума вдоль выбранной оси. Пример траектории поиска методом покоординатного спуска приведен на рис.1.
Достоинством метода является его простота, невысокие требования к памяти и сходимость практически с любых начальных приближений, если не попадет в овраг (может остановиться на дне оврага далеко от минимума). А основным недостатком – медленная сходимость. Установлено, что методом покоординатного спуска задача минимизации ф-ии будет решена за n шагов. Для общего вида – процесс бесконечный. Кажется разумным попытаться модифицировать этот метод т.о., чтобы на каждой итерации поиск производился не просто вдоль координатной оси, а вдоль наилучшего направления.
Метод Розенброка направлен на ликвидацию одного из недостатков метода покоординатного спуска — высокую чувствительность к выбору системы координат. Метод сводится по сути к отысканию «удачной» системы координат путем поворота исходных осей координат. После чего осуществляется поиск поочередно по всем переменным последовательно. Первый цикл поиска совпадает с Г.-З. А далее поворот в зависимости от вектора смещения точки поиска.
Симплексом в n- мерном пространстве называют фигуру, содержащую n+1 вершину. На плоскости – треугольник, в трехмерном пространстве – тетраэдр и т.д. Если все вершины симплекса равно удалены друг от друга, то такой симплекс называется регулярным.
В организации алгоритма поиска используется важное свойство симплекса: против каждой вершины находится одна грань.
Суть метода: в окрестности точки Х0 строится симплекс, затем находится самая плохая вершина, и на противоположной стороне строится новый симплекс, отличающийся только одной другая вершиной. Эта вершина получается симметричным отражением выбрасываемой вершины относительно центра противоположной грани. При выходе в район оптимума процесс обычно зацикливается, в этом случае нужно сжимать симплекс, откладывая вершину от грани на расстоянии вдвое меньше, чем необходимо. Процесс сжатия происходит многократно, до тех пор, пока размеры симплекса не будут меньше заданной величины. Недостаток – невозможность ускорения вдали от оптимума.
Методы градиентного спуска основываются на известном факте, что направление градиента показывает направление наискорейшего возрастания функции, а направление антиградиента, соответственно, показывает направление наискорейшего убывания функции. Модуль же градиента – характеризует скорость этого возрастания. Вектор градиента может быть получен через свои проекции на оси координат, которые равны соответствующим частным производным:
Градиент всегда перпендикулярен линии уровня, проходящей через ту точку, в которой вычислен градиент. Пример траектории поиска методом градиентного спуска приведен на рис..
Величина рабочего шага в направлении градиента зависит от величины градиента, которую заранее трудно учесть, поэтому, как правило, вводится коэффициент пропорциональности шага, с помощью которого можно управлять эффективностью (число повторов вычисления функции) метода.
Показано, что значение a можно определять по некоторым характеристикам функции f(x). Например, если существует такая константа R, что для любых точек
Однако, значения R и M обычно заранее неизвестны.
Разработаны различные методы, относящиеся к группе градиентного спуска. Среди них: с постоянным шагом, с дробным шагом и наискорейшег о спуска.
Основным недостатком градиентного метода является необходимость частого вычисления производных. Этого недостатка лишен метод наискорейшего спуска.
Особенность метода наискорейш его спуска в том, что в направлении антиградиента ищется точка, доставляющая минимум функции. Поиск этого минимума может производиться любым из известных методов одномерной минимизации.
Что такое пассивная стратегия поиска при численном решении задач многомерной безусловной оптимизации
5. Многомерная оптимизация
Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Количественная оценка оптимизируемого качества называется критерием оптимальности или целевой функцией. Её можно записать в виде:
Существуют два типа задач оптимизации – безусловные и условные.
Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (5.1) от n действительных переменных и определении соответствующих значений аргументов.
Решение задач оптимизации, в которых критерий оптимальности является линейной функцией независимых переменных (то есть содержит эти переменные в первой степени) с линейными ограничениями на них, составляет предмет линейного программирования.
Слово «программирование» отражает здесь конечную цель исследования – определение оптимального плана или оптимальной программы, по которой из множества возможных вариантов исследуемого процесса выбирают по какому-либо признаку наилучший, оптимальный, вариант.
Примером такой задачи является задача оптимального распределения сырья между различными производствами при максимальной стоимости продукции.
Пусть из двух видов сырья изготавливается продукция двух видов.
Учитывая, что расход данного ресурса не может превышать общего его количества, запишем ограничительные условия по ресурсам:
В аналогичном виде формулируются так называемые транспортные задачи (задачи оптимальной организации доставки товаров, сырья или продукции из различных складов к нескольким пунктам назначения при минимуме затрат на перевозку) и ряд других.
Графический метод решения задачи линейного программирования.
и условиям неотрицательности :
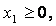
для которых функция
Построим в системе прямоугольных координат x 1 Ox 2 область допустимых решений задачи (рис.11). Для этого, заменяя каждое из неравенств (5.5) равенством, строим соответствующую ему граничную прямую:
а для координат любой точки В другой полуплоскости – противоположное неравенство:
Координаты любой точки граничной прямой удовлетворяют уравнению:
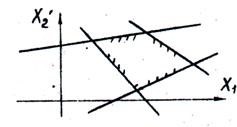
Для определения того, по какую сторону от граничной прямой располагается полуплоскость, соответствующая заданному неравенству, достаточно «испытать» одну какую-либо точку (проще всего точку О (0;0)). Если при подстановке её координат в левую часть неравенства оно удовлетворяется, то полуплоскость обращена в сторону к испытуемой точке, если же неравенство не удовлетворяется, то соответствующая полуплоскость обращена в противоположную сторону. Направление полуплоскости показывается на чертеже штриховкой. Неравенствам:
соответствуют полуплоскости, расположенные справа от оси ординат и над осью абсцисс.
На рисунке строим граничные прямые и полуплоскости, соответствующие всем неравенствам.
Общая, часть (пересечение) всех этих полуплоскостей будет представлять собой область допустимых решений данной задачи.
При построении области допустимых решений в зависимости от конкретного вида системы ограничений (неравенств) на переменные может встретиться один из следующих четырех случаев:
Рис. 12. Область допустимых решений пустая, что соответствует несовместности системы неравенств; решения нет
Рис. 14. Область допустимых решений ограниченная, изображается в виде выпуклого многоугольника. Допустимых решений бесконечное множество
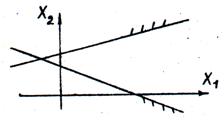
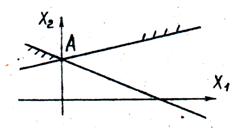
Рис. 15. Область допустимых решений неограниченная, в виде выпуклой многоугольной области. Допустимых решений бесконечное множество
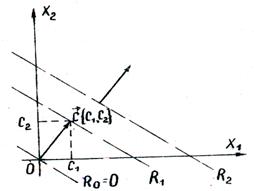
Графическое изображение целевой функции
Задача отыскания оптимального решения системы неравенств (5.5), для которого целевая функция R (5.7) достигает максимума, геометрически сводится к определению в области допустимых решений точки, через которую пройдет линия уровня, соответствующая наибольшему значении параметра R
Если область допустимых решений есть выпуклый многоугольник, то экстремум функции R достигается, по крайней мере, в одной из вершин этого многоугольника.
Если экстремальное значение R достигается в двух вершинах, то такое же экстремальное значение достигается в любой точке на отрезке, соединяющем эти две вершины. В этом случае говорят, что задача имеет альтернативный оптимум.
В случае неограниченной области экстремум функции R либо не существует, либо достигается в одной из вершин области, либо имеет альтернативный оптимум.
и условиям неотрицательности :
для которых функция:
Заменим каждое из неравенств равенством и построим граничные прямые:
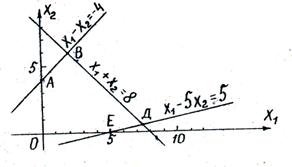
Определим полуплоскости, соответствующие данным неравенствам, путём «испытания» точки (0;0). С учетом неотрицательности x 1 и x 2 получим область допустимых решений данной задачи в виде выпуклого многоугольника ОАВДЕ.
В области допустимых решений находим оптимальное решение, строя вектор градиента
Задания. Найти положение точки экстремума и экстремальное значение целевой функции