что такое параметры модели в эконометрике
Виды эконометрических моделей
Главным инструментом эконометрического исследования является модель. Выделяют три основных класса эконометрических моделей:
Моделью временных рядов называется зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.
К моделям временных рядов, характеризующих зависимость результативной переменной от времени, относятся:
а) модель зависимости результативной переменной от трендовой компоненты или модель тренда;
б) модель зависимости результативной переменной от сезонной компоненты или модель сезонности;
в) модель зависимости результативной переменной от трендовой и сезонной компонент или модель тренда и сезонности.
К моделям временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени, относятся:
а) модели с распределённым лагом, объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных;
б) модели авторегрессии, объясняющие вариацию результативной переменной в зависимости от предыдущих значений результативных переменных;
в) модели ожидания, объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных.
Кроме рассмотренной классификации, модели временных рядов делятся на модели, построенные по стационарным и нестационарным временным рядам.
Стационарным временным рядом называется временной ряд, который характеризуется постоянными во времени средней, дисперсией и автокорреляцией, т. е. данный временной ряд не содержит трендовой и сезонной компонент.
Нестационарным временным рядом называется временной ряд, который содержит трендовую и сезонную компоненты.
Определение. Моделью регрессии с одним уравнением называется зависимость результативной переменной, обозначаемой как у, от факторных (независимых) переменных, обозначаемых как х1,х2,…,хn. Данную зависимость можно представить в виде функции регрессии или модели регрессии:
где β1…βk – параметры модели регрессии.
Можно выделить две основных классификации моделей регрессии::
а) классификация моделей регрессии на парные и множественные регрессии в зависимости от числа факторных переменных;
б) классификация моделей регрессии на линейные и нелинейные регрессии в зависимости от вида функции f(x,β).
В качестве примеров моделей регрессии с одним уравнением можно привести следующие модели:
а) производственная функция вида Q=f(L,K), выражающая зависимость объёма производства определённого товара (Q) от производственных факторов – от затрат капитала (К) и затрат труда (L);
б) функция цены Р=f(Q,Pk), характеризующая зависимость цены определённого товара (Р) от объема поставки (Q) и от цен конкурирующих товаров (Pk);
в) функция спроса Qd=f(P,Pk,I), характеризующая зависимость величины спроса на определённый товар (Р) от цены данного товара (Р), от цен товаров-конкурентов (Pk) и от реальных доходов потребителей (I).
Системой одновременных уравнений называется модель, которая описывается системами взаимозависимых регрессионных уравнений.
Системы одновременных уравнений могут включать в себя тождества и регрессионные уравнения, в каждое из которых могут входить не только факторные переменные, но и результативные переменные из других уравнений системы.
Регрессионные уравнения, входящие в систему одновременных уравнений, называются поведенческими уравнениями. В поведенческих уравнениях значения параметров являются неизвестными и подлежат оцениванию.
Основное отличие тождеств от регрессионных уравнений заключается в том, что их вид и значения параметров известны заранее.
Примером системы одновременных уравнений является модель спроса и предложения, в которую входит три уравнения:
а) уравнение предложения: =а0+а1*Рt+a2*Pt-1;
б) уравнение спроса: =b0+b1* Рt+b2*It;
в) тождество равновесия: QSt = Qdt,
где QSt – предложение товара в момент времени t;
Qdt – спрос на товар в момент времени t;
Рt – цена товара в момент времени t;
Pt-1 – цена товара в предшествующий момент времени (t-1);
It– доход потребителей в момент времени.
В модели спроса и предложения выражаются две результативные переменные:
а) Qt– объём спроса, равный объёму предложения в момент времени t;
б) Pt– цена товара в момент времени t.
Понятие эконометрической модели и последовательность ее построения



Хубулава Ное Михайлович
Учебник для студентов экономического профиля
всех специальностей и всех форм обучения, а также
на специалистов, занимающихся проблемами
экономического измерения, прогнозирования
Подписано в печать 10.05.2005. Формат 60×84 1/14.
Бумага офсетная. Печать офсетная. Уч. изд.
Лист 8,1. Тираж 5000.

Москва, Енисеевская 36.
— изучать реальное состояние объектов или процессов, выявлять и оценивать наиболее существенные факторы, определяющие поведение объекта исследования;
— прогнозировать изменение состояния объекта моделирования во времени.
Эконометрика как наука сформировалась и получила развитие на стыке экономической теории, математической и экономической статистики.
Экономическая теория предоставляет для эконометрики научное обоснование наличия и формы связи между явлениями и процессами. Однако, в отличие от экономической теории, эконометрику интересует не качественный анализ, а количественная оценка связей.
Эта оценка основывается на использовании методов математической статистики, и, прежде всего, корреляционно-регрессионного анализа. Информационной базой для построения моделей являются статистические данные. При построении эконометрической модели крайне важно знать способы получения и методики расчета показателей, поскольку в противном случае полученные на основе моделей выводы могут оказаться неточными. Кроме того, наличие статистической информации определяет конкретный состав используемых в модели показателей.
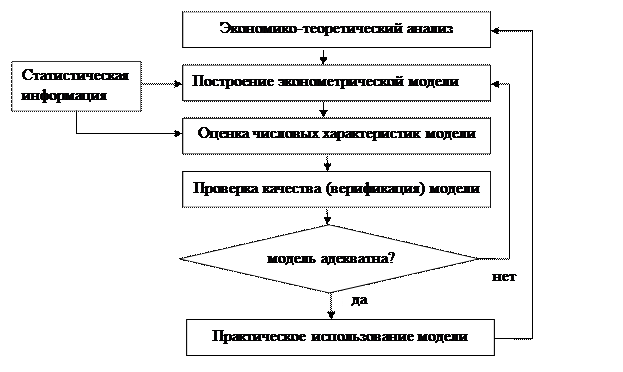
Процесс построения эконометрической модели можно представить следующим образом:
1.2. Эконометрическая модель: основные понятия.
Эконометрическая модель включает два вида переменных.
1. Переменные, характеризующие те экономические явления и процессы, которые требуется объяснить. Такие переменные принято называть зависимыми или объясняемыми и обозначать Y.
2. Переменные, характеризующие те процессы и явления, которые влияют на значение объясняемой переменной. Они называются независимыми или объясняющими и обозначаются Х1, Х2, Х3 и т.д.
Математически связь между зависимой и независимой переменными записывается в виде функции:
При наличии линейной связи между зависимой и независимой переменными, модель приобретает следующий вид:
В процессе эконометрического моделирования оценивается ожидаемое теоретическое значение зависимой переменной уt на основе выборочных данных:
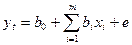
Например, при анализе стоимости жилья собрана информация по двум сотням различных квартир. По каждой их них определена цена квадратного метра, этаж, количество комнат и пр. Значение yt1 будет представлять собой цену квадратного метра в первой квартире, yt2 — во второй квартире так далее вплоть до yt200.
Аналогично определяются значения независимых переменных. Так, значение x11 будет представлять собой порядковый номер этажа в первой квартире, x12 — во второй квартире, значение x21 — количество комнат в первой квартире, x22 — во второй и т.д.
По результатам эконометрического анализа определяется усредненное влияние каждой из независимых переменных на зависимую посредством расчета величин b0, b1, b2 и т.д. Они называются параметрами модели.
Процедура оценивания эконометрических моделей, интерпретация и применение полученных результатов будут рассмотрены в последующих темах курса.
Введение в эконометрику, основы эконометрики, модели эконометрики
Рассмотрим такую ситуацию. Допустим, мы хотим продать автомобиль и даем объявление о продаже в газете. Естественно, перед любым человеком встает вопрос: какую цену указать в объявлении?
Очевидно, мы будем исходить из информации о цене, за которую продают подобные автомобили другие продавцы.
Что значит «подобные автомобили»? — Ясно, это автомобили, обладающие очень похожими значениями таких факторов, как год выпуска, мощность двигателя, пробег. Посмотрев колонку объявлений, мы формируем в голове свое мнение о рынке интересующего нас товара и, скорее всего, после некоторого размышления, назначаем цену. На этом простейшем примере на можно проследить важные моменты эконометрического моделирования.
Простой пример эконометрической модели
Рассмотрим вопрос в более общем виде. Мы ставим задачу определить цену — величину, которая формируется под воздействием некоторых факторов (года выпуска, мощность, пробег и т. д.). Такие величины обычно называются зависимыми (объясняемыми) переменными, а факторы, от которых они зависят, — объясняющими.
Формируя общее мнение о состоянии рынка, мы обращаемся к интересующему нас объекту и получаем ожидаемое значение зависимой переменной при заданных значениях объясняющих переменных.
На указанную цену — наблюдаемое значение зависимой переменной зависит также и от случайных явлений — таких, например, как характер продавца, его желание заработать денег, возможные сроки продажи автомобиля и др.
Продавец-одиночка вряд ли будет строить и анализировать какую-либо математическую модель, но менеджер крупного автосалона, специализирующегося на торговле на вторичном рынке, в большей степени, захочет иметь более точное представление об ожидаемой цене и о возможном поведении случайного фактора. Следующий шаг и есть эконометрическое моделирование.
Обобщающим моментом для любой модели в эконометрике является разбиение зависимой переменной на две части — объясненную и случайную. В эконометрике случайную переменную обозначают как Х, объясненную — Y. Сформулируем задачу моделирования самым общим, неформальным образом: на основании экспериментальных данных определить объясненную часть и, рассматривая случайную составляющую как случайную величину, получить оценки параметров ее распределения.
Таким образом, любая эконометрическая модель имеет следующий вид:
Практическое применение моделей в эконометрике
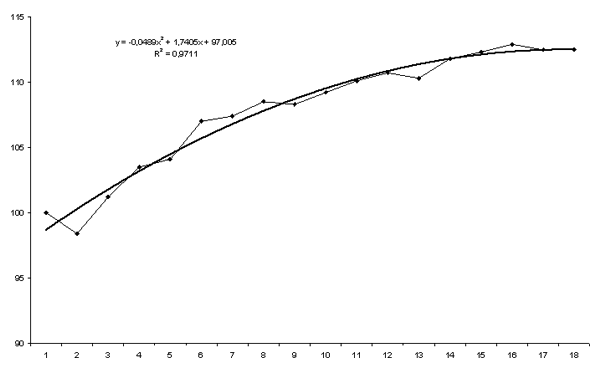
Во-первых, можно понять: как именно формируется (т.е. какие факторы включает) рассматриваемая экономическая переменная — цена на автомобиль.
Во-вторых, выявляется влияние каждой из объясняющих переменных (год, пробег … ).
В третьих, результат позволяет построить прогноз цены на автомобиль, если известны его основные параметры.
Источник: Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов, 2002. — 311 с
Задачи по эконометрике из книги Кремера решаются здесь
Модели эконометрики
Вы будете перенаправлены на Автор24
Понятие эконометрики
Эконометрика представляет собой область научного знания, которая выражает количественно взаимосвязи экономических процессов и явлений. Эконометрика является быстроразвивающейся научной отраслью, ее цель – придание количественной меры экономическим отношениям.
Понятие эконометрика было впервые использовано австро-венгерским бухгалтером П. Цьемпой, затем в 1930 году было основано эконометрическое общество в ходе заседания Американской ассоциации развития науки, а норвежский исследователь Р. Фриш назвал новую науку «эконометрика». Эконометрика – это комбинация двух слов «экономики» и «метрики». Таким образом, термин выражает специфику и содержание эконометрики: количественное выражение соотношений и связей, раскрытых и обоснованных экономической теорией.
Эконометрика является комбинацией трех научных областей: экономической статистики, экономической теории и математической статистики.
Эконометрика использует конкретные экономические данные и количественно описывает конкретные взаимосвязи, другими словами, заменяет коэффициенты в общем виде конкретными значениями.
Многие эконометрические методы и приемы заимствованы из математической статистики. Между тем, математико-статистические методы являются универсальными и учитывают специфику экономических данных.
К особенностям измерений в экономике можно отнести следующее:
Готовые работы на аналогичную тему
Поэтому часто в экономических данных содержатся ошибки. Областью эконометрики является разработка специальных методов анализа, позволяющих, если не устранить, то добиться снижения влияния этих неточностей на получаемые результаты.
Модели эконометрики
Эконометрическая модель представляет собой вероятностно-статистическую модель, которая описывает механизм функционирования социально-экономической или же экономической системы.
Все эконометрические модели подразделяются на три класса:
Регрессионная модель, имеющая одно уравнение:
Системы уравнений одновременного типа. Данные модели можно описать с помощью систем взаимосвязанных регрессионных уравнений. Такая система позволяет объяснить, а также спрогнозировать такое количество результативных признаков, которое равно уравнениям, входящим в систему. Уравнения в системе могут быть тождествами или же поведенческими уравнениями.
Модели временных показателей. В данных моделях результативный признак – это функция переменной времени или переменных, которые относятся к другим временным моментам.
Моделями временных данных, являющихся зависимостью результативного признака от периода времени, могут быть:
Моделями временных данных, которые выражают зависимость результативных признаков от переменных, относящихся к другим временным моментам, являются:
Этапы эконометрического анализа
Эконометрический анализ как правило проводится в шесть этапов. Рассмотрим каждый из них.
На первом этапе (постановочном) формируются цели исследования, определяются участвующие в модели экономические переменные. Прежде чем выбрать экономические переменные, необходимо каждую из них теоретически обосновать. Объясняющие переменные не должны находиться в тесной корреляционной или функциональной зависимости, поскольку это может вызвать мультиколлинеарность.
На втором этапе (априорном) анализируется сущность изучаемого объекта, формируется и формализуется априорная, т.е. известная до начала моделирования, информация.
На четвертом этапе (информационном) собирается необходимая статистическая информация – наблюдаемые значения экономических переменных.
На пятом этапе (идентификации модели) проводится статистический анализ исследуемой модели и оцениваются ее параметры.
На заключительном этапе верификации модели проверяется ее истинность и адекватность. Определяется точность расчетов для данной модели, степень соответствия построенной модели моделируемому экономическому процессу или объекту. При наличии статистических данных, характеризующих моделируемый экономических процесс в предшествующий или данный момент времени, то, чтобы верифицировать модель, построенную для прогноза, необходимо провести сравнение реальных значений переменных в последующий момент времени со значениями, которые получены на основании рассматриваемой модели.
Что такое параметры модели в эконометрике
1.1. Понятие математической модели и математического моделирования
Эконометрический подход к изучению и анализу социально-экономических объектов (явлений, процессов, систем) предполагает построение модели изучаемого объекта. Это является ключевым моментом при использовании эконометрического подхода. В эконометрике модель относится к классу математических моделей.
Под математической моделью понимают приближенное описание объекта (процесса, явления, системы) на языке математики.
Язык математики (математический аппарат, инструментарий) включает такие средства описания, как таблицы, графики, алгебраические и логические соотношения, неравенства, дифференциальные или разностные уравнения, теоретико-множественное описание и т.п. и т.д.
Необходимость построения и использования математических моделей обусловлена следующими важными обстоятельствами:
1. процесс построения математической модели позволяет систематизировать сложные, взаимосвязанные факторы, выделить существенные и не существенные для изучаемого процесса связи и параметры;
2. математическое описание позволяет каждому фактору поставить в соответствие математический символ (переменную) и установить взаимосвязь и взаимовлияние одних переменных на другие;
3. математическая модель в отличие от вербальной (словесной) позволяет описать процесс компактно, в виде набора математических соотношений, абстрагируясь при этом от несущественных деталей и установить строгие правила поведения переменных, характеризующих процесс;
4. при построении математической модели упорядочивается информация, определяется ее ценность и необходимый объем;
5. математическая модель дает основу для количественного анализа поведения объекта путем проведения численного (имитационного) эксперимента, что позволяет выявить возможные альтернативные сценарии поведения объекта и количественно оценить последствия, к которым приведет их реализация. Это особенно важно при изучении систем, для которых невозможен натурный эксперимент. К таким системам относятся и социально-экономические системы и процессы. При этом во много раз увеличивается число сценариев, которые удается проанализировать;
6. математическая модель дает возможность качественного анализа поведения изучаемого объекта. Другими словами, построив математическую модель, ее можно изучать в соответствии с правилами математики, абстрагируясь от реального объекта. Это часто позволяет получить новые, нетривиальные знания о самом моделируемом объекте;
7. математическое моделирование позволяет выявить и оценить влияние скрытых (латентных) факторов;
8. построение математической модели является основой для эффективного применения современных информационных технологий. Необходимость их применения обусловлена сложностью используемых математических моделей, необходимостью сбора и обработки больших массивов данных, сложностью вычислительных процедур;
Процесс построения математической модели включает следующие основные этапы:
1. Формулировка цели исследования, качественный анализ и изучение экономического объекта (предметной области), установление общих закономерностей его функционирования, формулировка правдоподобных гипотез и предположений (упрощающих допущений) относительно характера взаимодействия различных элементов объекта и т.д.
2. Анализ и оценка качества имеющихся эмпирических данных. Изучение возможностей получения дополнительной информации и, если необходимо, ее сбор.
3. Построение математической модели с привлечением математического аппарата, позволяющего адекватно описать поведение объекта.
4. Оценка параметров модели (идентификация) на основе имеющихся статистических данных. Проверка адекватности модели (ее соответствия данным).
5. Формальный анализ математической модели, изучение ее свойств с целью изучения поведения объекта на качественном уровне.
6. Проведение численных расчетов (экспериментов) и получение количественных результатов.
7. Анализ полученных результатов и их содержательная (экономическая) интерпретация. Выработка рекомендаций для принятия решений.
Современная математика дает богатый арсенал средств для построения математических моделей в естественных науках, технике, экономике и других гуманитарных науках, подкрепленный возможностями современных автоматизированных информационных технологий.