что такое парамагнетизм и диамагнетизм
Парамагнетизм и диамагнетизм
Рассмотрите природу и действие парамагнетизма и диамагнетизма: силы притягивания и отталкивания в магнитном поле, определения, примеры, магнитная сила.
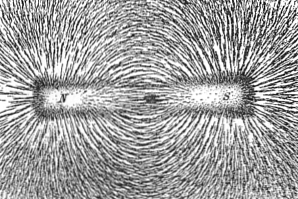
Парамагнетизм – притягивание материала в магнитном поле, а диамагнетизм – отталкивание.
Задача обучения
Основные пункты
Термины
Парамагнетизм
Атомы и молекулы обладают постоянными магнитными моментами (диполи) даже, если приложенное поле отсутствует. Обычно постоянный момент гарантируется вращением неспаренных электронов на атомных и молекулярных электронных орбиталях.
В условиях чистого парамагнетизма диполи не контактируют и ориентируются беспорядочно при термическом возбуждении, если нет внешнего поля. То есть, чистый магнитный момент приближается к нулю. Когда же магнитное поле активировано, то диполи стараются выровняться и формируют чистый магнитный момент в сторону приложенного поля.
Парамагнитные материалы обладают небольшой положительной восприимчивостью к магнитным полям. Они лишь немного притягиваются и не сохраняют приобретенных свойств, если нет внешнего поля.
Ориентация в парамагнитном материале при наличии электрического поля (справа) и его удалении (слева)
Среди парамагнитных материалов стоит вспомнить магний, молибден, литий и тантал. Однако, как только внешнее магнитное поле исчезает, парамагнетики теряют свои свойства, потому что тепловое движение рандомизирует вращательные позиции. Некоторые сохраняют вращательный беспорядок при абсолютном нуле. Поэтому и суммарная намагниченность опускается к нулю, если убрать поле.
Диамагнетизм
Диамагнетизм отмечает умение объекта формировать магнитное поле, вступающее в сопротивление к внешнему. Поэтому они не притягиваются, а отталкиваются, что приводит к таким поразительным вещам, как левитация диамагнитного материала, если его установить над мощным магнитом.
Пиролитический углерод, левитирующий над постоянным магнитом
По большей части диамагнетизм присутствует во всех материалах, и он всегда слабо влияет на реакцию материала по отношению к магнитному полю. У всех проводников заметен эффективный диамагнетизм, если магнитное поле меняется. К примеру, сила Лоренца на электронах заставит их циркулировать вокруг вихревых токов. Далее токи создадут индуцированное магнитное поле, сопротивляющееся перемещению проводника.
Что такое парамагнетизм и диамагнетизм
Магнетизм свободного атома имеет 3 главных источника: спин электронов; их орбитальный момент; и изменение в орбитальном моменте, индуцированном внешним магнитным полем. Не подтвердившееся представление о неких магнитных зарядах (монополи Дирака не обнаружены до настоящего времени) оказалось, тем не менее, удобной абстракцией. В частности, по аналогии с кулоновским взаимодействием, силу взаимодействия двух магнитных зарядов m1 и m2 можно записать как
при этом сила действующая на заряд m в поле H,
Магнитный момент диполя определяется как

L = [H
На магнитный момент, помещенный в неоднородное магнитное поле, действует сила F = (
M = 

Коэффициент пропорциональности 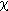
M = 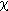
При нарушении линейной зависимости между М и Н:
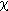
В общем случае 
B = H + 4
B = 
Коэффициент пропорциональности 
B = 
называется магнитной проницаемостью (permeability). Из предыдущего следует


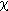


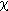
Восприимчивость диамагнетиков, парамагнетиков, ферромагнетиков и ферримагнетиков
Энергия магнита, имеющего магнитный момент 

Намагниченность, т.е. магнитный момент единицы объема M(Н), при T = 0
M0(H)=1/V 

Формулу (12.15) можно также записать в виде т.д. соотношения
Дифференциальная восприимчивость определяется как
Гамильтониан взаимодействия атомов и молекул с магнитным полем, расщепление уровней
В однородном магнитном поле гамильтониан изменяется следующим образом
1. Импульс
pi
Векторный потенциал выбираем в виде
rot A


2. В гамильтониан H должна быть включена энергия взаимодействия поля со спином


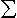
Формулу (12.24) можно представить в виде
T = T0 + 
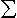

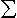
Объединяя (12.25) и (12.23), получаем, что зависимость от поля определяется следующими членами в гамильтониане:


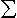
Изменение энергии (12.27) оказывается малым по сравнению с энергией атомных возбуждений, поэтому применима теория возмущений. Поскольку восприимчивость
Подставляя (12.27) в (12.28) и учитывая только линейные и квадратичные члены по H, получаем
Выражение (12.29) лежит в основе теоретического описания восприимчивости отдельных атомов, ионов и молекул. На нем базируется также теория восприимчивости ионных и молекулярных кристаллов, т.е. тех тв. тел, которые могут быть представлены как совокупность слабо деформированных свободных ионов. В этих случаях восприимчивость вычисляется посредством суммирования вкладов отдельных ионов.
Линейный член в (12.29) почти всегда будет доминировать, даже при очень сильных полях (
10 4 Гc), если, конечно, он не обращается в 0. В этом случае




10 4 Гс эта величина
эВ).
В третьем члене в (12.29) 2 + yi 2 )|n> имеет порядок типичного атомного размера, поэтому
(e 2 /8mc 2 )H 2 2 + yi 2 )|n> = O[(eH/2mc) 2 ma0 2 ] 

Поскольку e 2 /a0 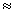
10 5 раз, даже в сильных полях
Ларморовский диамагнетизм атомов с полностью заполненными внутренними оболочками

Если при т.-д. равновесии вероятность обнаружить ион в каком-либо состоянии, отличном от основного, пренебрежимо мала (это условие выполняется практически при всех не очень высоких температурах), то восприимчивость тв.тела, состоящего из N-ионов, определяется выражением
Это формула Ланжевена (P. Langevin, 1905) для т.н. ларморовского диамагнетизма. Величины 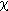
Диамагнетизм является универсальным свойством, присущим всем веществам. Ларморовский диамагнетизм ассоциируется со стремлением электрических зарядов экранировать внутренний объем тела от воздействия прилагаемого магнитного поля, аналогично закону Ленца (наведенный ток препятствует изменению электрического потока через контур). В создании диамагнитного момента участвуют все электроны атома, а также свободные носители. Поэтому, матричный элемент в (12.33) нормируют на полное число электронов
а 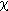
Отсюда следует, что 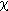
Поскольку, величина 2 > = 2 > + 2 > = 2/3 ( 2 > + 2 > + 2 >) = 2/3 2 > и тогда диамагнитная восприимчивость единицы объема:
что совпадает с (12.35).
Парамагнетизм ( 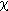
Парамагнетизм атомов с частично заполненной оболочкой.
Рассмотрим 2 случая.
1. Парамагнетизм Ван Флека. Полный угловой момент J=0. Это имеет место, например, в случае заполнения оболочки на 1 электрон меньше, чем наполовину заполненная (L = l, S = 2l x 1/2 = l, J = |L-S| = 0). Основное состояние не вырождено (кратность 2J + 1 = 1). Линейный член в (12.29) обращается в нуль (J = 0), как и в случае заполненной оболочки. Однако, в отличие от этого, 2-й член в (12.29) не должен обращаться в нуль. Т.е. в этом случае (12.29) имеет вид
В противном случае ближайшие по энергии мультиполи J
Парамагнетизм Ван Флека связан с возможностью перехода из возбужденных (деформированных, поляризованных) состояний в основное состояние системы слабовозбужденных атомов, молекул, у которых оболочки не обладают сферической симметрией. Вещества, содержащие парамагнитные ионы с синглетным основным состоянием, называются поляризационными или ванфлековскими парамагнетиками.
Решение задачи упрощается, если использовать теорему Вигнера-Эккарта, согласно которой матричный элемент любого векторного оператора в (2J+1)-мерном пространстве собственных функций операторов J 2 и Jz при заданном значении J пропорциональны матричным элементам оператора J. Отсюда
Важное свойство этого результата заключается в том, что коэффициент пропорциональности g(JLS) не зависит от Jz и Jz‘. В частности, поскольку матричные элементы оператора Jz имеют вид
‘ >=Jz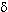
‘ > = g(JLS)Jz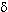
Формула (12.45) имеет эквивалентное операторное представление:

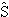
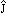
Отметим, что это соотношение справедливо только в пределах (2J + 1)-мерного множества состояний, образующих вырожденное основное состояние атома в отсутствие поля. Т.е. (12.51) имеет смысл только для матричных элементов перехода между состояниями с одинаковыми J,L,S. Если расстояние между основным и первым возбужденным мультиплетами велико по сравнению с kBT (что бывает часто), то заметный вклад в свободную энергию вносят только (2J + 1) состояний мультиплета основного состояния. В этом (и только в этом) случае можно считать, исходя из (12.51), что первый член в (12.29) отражает взаимодействие типа (-
Из-за того, что в отсутствие поля основное состояние вырождено, ни в коем случае нельзя вычислять восприимчивость, приравнивая двойную производную свободной энергии основного состояния (как это мы делали в (12.42)), поскольку при H 
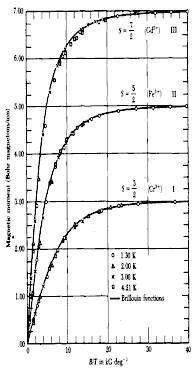 Рис. 12.1. Функция Бриллюэна |
exp(- 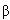
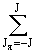
Отсюда получаем, что намагниченность
— закон Кюри-Бриллюэна (Curie-Brillouin)



Экспериментально закон
При больших J
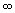
при gJ
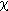

— эффективное число магнетонов Бора
Ce 3+ 4f 2 5s 2 p 6 2 F(L = 3)5/2 p(теор) = 2.54, р(эксп)=2.4;
Pr 3+ 4f 2 5s 2 p 6 3 H(L = 4)4 р(теор) = 3.58, р(эксп)=3.5.
Однако имеется достаточно большое расхождение для некоторых РЗ элементов
Sm 3+ 4f 5 5s 2 p 6 6H5/2 р(теор) = 0.84, р(эксп) =1.5;
Pr 3+ 4f 6 5s 2 p 6 7F0 р(теор) = 0, р(эксп) =3.4
Расхождение показывает, что необходимо учитывать влияние более высоких уровней L-S мультиплета, поскольку расстояние между мультиплетными уровнями оказывается не очень большим по сравнению с kBT при к.Т. В результате при данных L и S возбуждаются состояния с различными J, которые перемешиваются.
Парамагнетизм группы железа.
Как показывает сопоставление магнитных моментов (чисел магнетонов р), расчитанных по закону Кюри-Бриллюэна (12.55)
M


Расщепление внутрикристаллическим полем
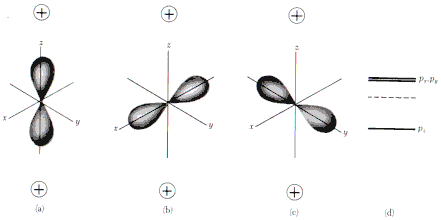
Рис.12.2. Расщепление уровней внутрикристаллическим полем (Ch.K. 14.6)
Замораживание орбитального углового момента.
Парамагнитная и диамагнитная восприимчивость электронов проводимости
 Рис. 12.3. Парамагнетизм Паули |
S ↑↑ H 


Число электронов в единице объема
n 
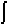
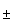
Электроны с параллельными и антипараллельными направлениями спина перераспределяются так, что на поверхности Ферми их энергии равны.
g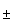
n 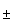
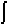
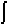
При этом из (12.73) следует n = 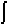
Из (12.69) и (12.75) получаем
M = 
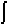
или, интегрируя по частям,
M = 
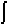


M = 
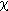

1/T).
В случае свободных электронов g(EF) = mkF/ 

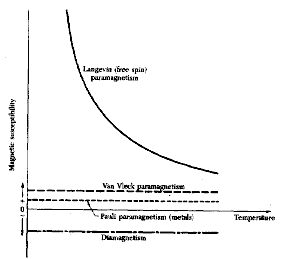 Рис. 12.4. (Ch.K) Температурная зависимость χ (T) |
Энергия уровней системы в магнитном поле, согласно (12.13) составляет
U = +
соответсвенно, уровни расщепляются на величину 

N1/N = exp(


N2/N = exp(-


Связь Рассела-Саундерса (L-S связь)
Правило Рассела-Саундерса состоит а утверждении, что полный орбитальный момент атома J формируется как сумма полных орбитальных моментов и полных спинов электронов, т.е.
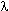
Для одиноких на орбите электронов λ > 0. Для оболочек, заполненных более чем на половину, λ λ λ > 0 выгодно состояние с минимальным значением J (орбитальный момент антипараллелен спиновому).
Таблица 12.2 Схема формирования основных состояний ионов с частичн заполненными d- и f- оболочками, в соответствии с правилами Хунда.
Причины парамагнетизма, парамагнитные материалы, примеры и различия с диамагнетизмом
парамагнетизм это форма магнетизма, при которой некоторые материалы слабо притягиваются внешним магнитным полем и образуют внутренние магнитные поля, индуцированные в направлении приложенного магнитного поля.
Вопреки тому, что часто думают многие, магнитные свойства не сводятся только к ферромагнитным веществам. Все вещества обладают магнитными свойствами, хотя и в более слабой форме. Эти вещества называются парамагнитными и диамагнитными.
Таким образом, можно выделить два типа веществ: парамагнитный и диамагнитный. В присутствии магнитного поля парамагнитные притягиваются к области, где интенсивность поля больше. Напротив, диамагнитные притягиваются к области поля, в которой интенсивность ниже.
Находясь в присутствии магнитных полей, парамагнитные материалы испытывают такой же вид притяжения и отталкивания, как и магниты. Однако, когда магнитное поле исчезает, энтропия прекращает магнитное выравнивание, которое было вызвано.
Другими словами, парамагнитные материалы притягиваются магнитными полями, хотя они не превращаются в постоянно намагниченные материалы. Некоторые примеры парамагнитных веществ: воздух, магний, платина, алюминий, титан, вольфрам и литий, среди других.
причины
Парамагнетизм связан с тем, что некоторые материалы состоят из атомов и молекул, которые имеют постоянные магнитные моменты (или диполи), даже когда они не находятся в присутствии магнитного поля.
Магнитные моменты вызваны спинами неспаренных электронов металлов и других материалов, обладающих парамагнитными свойствами..
При чистом парамагнетизме диполи не взаимодействуют друг с другом, а ориентируются случайным образом в отсутствие внешнего магнитного поля вследствие теплового возбуждения. Это генерирует нулевой магнитный момент.
Однако когда магнитное поле приложено, диполи имеют тенденцию выравниваться с приложенным полем, что приводит к суммарному магнитному моменту в направлении указанного поля и добавлению к внешнему полю..
В любом случае выравниванию диполей можно противодействовать под воздействием температуры.
Таким образом, когда материал нагревается, термическое перемешивание способно противодействовать влиянию магнитного поля на диполи, а магнитные моменты хаотично переориентируются, уменьшая напряженность индуцированного поля..
Закон Кюри
Закон Кюри был экспериментально разработан французским физиком Пьером Кюри в 1896 году. Его можно применять только при наличии высоких температур и при наличии парамагнитного вещества в присутствии слабых магнитных полей..
Это так, потому что он не может описать парамагнетизм, когда большая часть магнитных моментов выровнена.
Закон гласит, что намагниченность парамагнитного материала прямо пропорциональна приложенной напряженности магнитного поля. Это то, что известно как закон Кюри:
Из наблюдения закона Кюри также следует, что намагниченность обратно пропорциональна температуре. По этой причине, когда материал нагревается, диполи и магнитные моменты имеют тенденцию терять ориентацию, приобретаемую присутствием магнитного поля..
Парамагнитные материалы
В физическом выражении утверждается, что его относительная магнитная проницаемость (отношение между проницаемостью материала или среды и проницаемостью вакуума) приблизительно равна 1, что является магнитной проницаемостью вакуума..
Среди парамагнитных материалов есть особый тип материалов, который называется суперпарамагнитным. Хотя они следуют закону Кюри, эти материалы имеют довольно высокое значение постоянной Кюри.
Различия между парамагнетизмом и диамагнетизмом
Именно Майкл Фарадей в сентябре 1845 года осознал, что в действительности все материалы (не только ферромагнетики) реагируют в присутствии магнитных полей..
Как парамагнитные, так и диамагнитные материалы обладают слабой восприимчивостью к магнитным полям, но, хотя в первой она положительна, во второй она отрицательна.
Диамагнитные материалы слегка отталкиваются магнитным полем; С другой стороны, парамагнитные притягиваются, хотя и с небольшой силой. В обоих случаях, когда магнитное поле удалено, эффекты намагниченности исчезают.
Как уже было сказано, подавляющее большинство элементов, составляющих периодическую таблицу, являются диамагнитными. Так, примерами диамагнитных веществ являются вода, водород, гелий и золото.
приложений
Поскольку парамагнитные материалы имеют вакуумоподобное поведение в отсутствие магнитного поля, их применение в промышленности несколько сокращается..
Одним из наиболее интересных приложений парамагнетизма является электронный парамагнитный резонанс (РПЭ), который широко используется в физике, химии и археологии. Это спектроскопический метод, с помощью которого можно обнаружить частицы с неспаренными электронами.
Этот метод применяется в ферментации, в промышленном производстве полимеров, для износа моторных масел и в производстве пива, а также в других областях. Точно так же этот метод широко используется при датировке археологических памятников..