что такое параллельное проектирование

Вопрос 1. Понятие параллельного проектирования

Тема. Параллельное проектирование.

Изображение пространственных фигур

Вопрос 1. Понятие параллельного проектирования.

Вопрос 2. Свойства параллельного проектирования.

Вопрос 3. Изображение пространственных фигур.

Вопрос 4. Практическая часть (решение задач).

Домашнее задание.

Вопрос 1. Понятие параллельного проектирования

В стереометрии большое значение имеет умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости пространственные фигуры.

Итак, зачастую для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование. Определяется оно следующим образом.

Пусть — некоторая плоскость,

— некоторая прямая, пересекающая эту плоскость.

Возьмём в пространстве произвольную точку .

Если точка не лежит на прямой , то проведём через точку прямую, параллельную прямой , и обозначим через точку пересечения этой прямой с плоскостью .

Если же точка лежит на прямой , то обозначим через точку пересечения прямой с плоскостью .

Точка называется проекцией точки на плоскость при проектировании параллельно прямой (или параллельной проекцией точки ).

Плоскость называется плоскостью проекций, а о прямой говорят, что она задаёт направление проектирования.

Все прямые, параллельные прямой , задают одно и то же направление проектирования, поэтому также называются проектирующими прямыми.

Примеры параллельных проекций дают, например, тени предметов под воздействием пучка параллельных солнечных лучей.

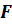
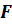
Пусть — плоская или пространственная фигура. Проекцией фигуры на плоскость при проектировании параллельно прямой называется множество проекций всех точек фигуры .

Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.

Источник

СОДЕРЖАНИЕ

Вступление

Вторая концепция заключается в том, что все действия по проектированию должны выполняться одновременно, т. Е. Одновременно. Идея состоит в том, что одновременный характер этих действий значительно увеличивает производительность и качество продукции. Таким образом, ошибки и изменения могут быть обнаружены на ранних этапах процесса проектирования, когда проект еще остается гибким. Обнаруживая и исправляя эти проблемы на раннем этапе, группа разработчиков может избежать ошибок, которые часто становятся дорогостоящими, поскольку проект переходит к более сложным вычислительным моделям и, в конечном итоге, к фактическому производству оборудования.

Параллельное проектирование заменяет более традиционный последовательный процесс проектирования, или «модель водопада». В Concurrent Engineering вместо этого используется итеративный или интегрированный метод разработки. Метод водопада движется линейно, начиная с требований пользователей и последовательно продвигаясь к проектированию и внедрению, пока у вас не будет готового продукта. В этой системе проектирования команда дизайнеров не будет быстро оглядываться назад или вперед с того шага, на котором она находится, чтобы исправить или предвидеть проблемы. В случае, если что-то пойдет не так, дизайн обычно нужно пересмотреть или сильно изменить. Параллельный или итеративный процесс проектирования способствует быстрому изменению стратегии, так что учитываются все аспекты жизненного цикла продукта, что позволяет использовать более эволюционный подход к проектированию. Разницу между двумя процессами проектирования можно увидеть графически на рисунке 1.

Значительная часть метода параллельного проектирования заключается в том, что отдельному инженеру предоставляется гораздо больше права голоса в общем процессе проектирования из-за совместной природы параллельного проектирования. Утверждается, что наделение дизайнера правом собственности способствует повышению производительности труда сотрудников и качества продукта, исходя из предположения, что люди, которым дано чувство удовлетворения и ответственности за свою работу, как правило, работают усерднее и создают более надежный продукт, а не сотруднику, которому поручена задача, которая мало влияет на общий процесс.

Проблемы, связанные с параллельным проектированием

Существуют поставщики услуг, которые специализируются в этой области, не только обучая людей эффективному параллельному проектированию, но и предоставляя инструменты для улучшения взаимодействия между членами команды.

Элементы

Кросс-функциональные команды

Кросс-функциональные группы включают людей из разных областей рабочего места, которые все вовлечены в определенный процесс, включая производство, проектирование оборудования и программного обеспечения, маркетинг и т. Д.

Параллельная реализация продукта

Одновременное выполнение нескольких задач, например одновременное проектирование различных подсистем, имеет решающее значение для сокращения времени проектирования и лежит в основе параллельного проектирования.

Дополнительный обмен информацией

Дополнительный обмен информацией помогает свести к минимуму вероятность того, что параллельная реализация продукта приведет к неожиданностям. «Инкрементальный» означает, что как только новая информация становится доступной, она передается и интегрируется в дизайн. Межфункциональные группы важны для эффективного и своевременного обмена информацией.

Комплексное управление проектами

Интегрированное управление проектом гарантирует, что кто-то несет ответственность за весь проект, и эта ответственность не передается после выполнения одного из аспектов работы.

Определение

Используются несколько определений параллельной разработки.

Использование CE

В настоящее время CE используют несколько компаний, агентств и университетов. Среди них можно отметить:

Источник

Реферат по теме Параллельное проектирование.

Ищем педагогов в команду «Инфоурок»

Оглавление

Введение

Я выбрал данную тему потому что передо мной стояла задача научиться быстро и точно производить различные построения. Актуальность темы заключается в том, что построение сечение широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники, а в школьном курсе геометрии решение такого типа задач уделяется очень мало времени. В работе были использованы задачи, теоремы, аксиомы, свойства, которые являются методами и приемами изучения данной темы.

Целью моей работы было исследование и приминение свойств параллельного проектирования при изображениии фигур на плоскости и при построении сечений многогранников.

Геометрические задачи традиционно делятся на три типа:

2. на доказательство;

1. Основные понятия теории изображения фигур

1.1. Параллельное проектирование и его свойства.

Параллельное (цилиндрическое) проецирование можно рассматривать как частныйтслучай центрального проецирования с несобственным центром. Здесь предмет рассматривают с бесконечно удаленной точки зрения.

Чертежи геометрических образов в ортогональных проекциях широко применяются в начертательной геометрии. Они просты в построениях, дают возможность легко производить различные измерения геометрических образов и определять взаимоположение отдельных элементов.

Множество F о проекций точек данной фигуры F на плоскость По называется проекцией фигуры F на плоскость По.

Легко показать, что параллельное проецирование, как отображение множества точек пространства во множество точек плоскости По, обладает свойствами

1. Проекцией прямой l является прямая l о, если , если то проекцией прямой l является точка L о, где ( L о) = l ∩ По.

2. Проекцией параллельных прямых являются параллельные прямые или совпавшие прямые, или две точки.

3. Коллинеарные точки А, В, С проектируются в коллинеарные точки Ао, Во, Со.

4. Неколлинеарные точки А, В, С, лежащие в плоскости П, не параллельной вектору р, проектируются в неколлинеарные точки Ао, Во, Со.

5. Сохраняется отношение «лежать между» для трех коллинеарных точек А, В, С, если

6. Сохраняется простое отношение трех точек А, В, С, если

7. Если отрезок (луч) АВ не параллелен вектору р, то проекцией АВ является отрезок (луч) АоВо (рис.3)

8. Проекцией пересекающихся прямых являются пересекающиеся прямые или совпадающие прямые.

9. Проекцией скрещивающихся прямых являются пересекающиеся прямые или параллельные прямые, или совокупность точки и прямой (рис. 4а, 46, 4в).

10. Проекцией угла АВС является угол АоВоСо в общем случае ему неравный. (плоскость АВС || р ).

1.2. Требования к чертежу

Я установил, что первым и важнейшим шагом решения геометрической задачи является построение чертежа, соответствующего условию. Если задача планиметрическая, то чертеж является либо копией оригинала, либо ему подобен. При изображении пространственных фигур возникают трудности, ибо не может плоская фигура быть подобной пространственной. Чертеж должен удовлетворять некоторым требованиям, способствующим наилучшему восприятию изображения пространственной фигуры.

Прежде всего, чертеж должен быть верен, т, е. представляет собой фигуру, подобную произвольной параллельной проекции оригинала. При этом естественно должны выполняться все свойства параллельного проецирования. При проецировании устанавливается геометрическая (проективная) связь между оригиналом и проекцией. Геометрические образы (формы) содержат в себе свойства, сохраняющиеся в проекциях.

Если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией точки в том же отношении.

Точка пересечения проекций пересекающихся прямых линий является проекцией точки пересечения этих прямых линий.

Проекции отрезков параллельных прямых линий параллельны и имеют одно направление, а длины их находятся в таком же отношении, как и длины самих отрезков.

Проекции отрезков двух скрещивающихся прямых линий в зависимости от направления проецирования могут или пресекаться, или быть параллельными.

При прямоугольном проецировании прямой угол между отрезками прямых проецируется без искажения(прямым углом), если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна к ней.

Во-вторых, чертеж должен быть наглядным, т. е. дающим пространственное представление об оригинале. С этой целью на изображении помимо очертания рассматриваются видимые и невидимые линии. Сравните восприятие рис. 6 и 7.

Наконец, чертеж должен быть легко выполним циркулем и линейкой, его построение должно удовлетворять аксиомам конструктивной геометрии. Однако разделы «Геометрические построения на плоскости» и «Методы изображений» так далеко стоят друг от друга, что при изучении одного мы совершенно забываем об изученном ранее другом.

1.3. Изображение плоских фигур в параллельной проекции

При изображении плоских фигур в параллельной проекции применяются следующие теоремы.

Изображением является любой треугольник АВС.

Если дано изображение на плоскости П, то можно построить изображение любой точки .

Исходя из теорем 1 и 2, легко построить изображения любых плоских фигур; в частности, изображением параллелограмма (квадрата, ромба, прямоугольника) является любой параллелограмм. Изображением трапеции является трапеция с тем же отношением длин оснований. Изображением окружности является эллипс, изображением перпендикулярных диаметров окружности являются сопряженные диаметры эллипса.

Ввиду того, что при изображении сферы, цилиндра, конуса необходимо уметь строить изображение окружности, я остановлюсь немного подробнее на способах построения эллипса.

Способ I. Построение эллипса по двум главным диаметрам АВ и C Д (рис. 8).

1. АВ ∩ СД = О, О- середина отрезка АВ

3.

Способ П. Построение эллипса по двум сопряженным диаметрам, используя перспективно аффинные преобразования плоскости (рис. 9).

Пусть АВ и CD — два сопряженных диаметра эллипса. Я построю на диаметре АВ окружность и проведу диаметр С ₁ D ₁ ей перпендикулярный. Применяю перспективно аффинное преобразование, заданное осью АВ и парой соответствующих точек С1 → С (или D ₁ → D ). Тогда образом окружности будет эллипс.

4.

1.4 Задание многогранников.

1.5. Изображение пространственных фигур в параллельной проекции

При изображении пространственных фигур в параллельной проекции применяют теорему Польке-Шварца. Всякий полный невыраженный четырехугольник АВС D вместе с его диагоналями можно рассматривать как изображение тетраэдра любой наперед заданной формы

Используя теорему Польке-Шварца и свойство параллельного проецирования, я показываю, что изображением призмы и, цилиндра и конуса являются фигуры.

2. Методы построения сечений многогранников

2.1. Метод следов

6. Пункты 4-5 повторить для вершин В1, С1. нижнего основания фигуры F ;

7. — искомое сечение.

Фактически где f гомология, заданная осью s и парой точек М ₁ → М или N ₁ → N, или К ₁ → К.

Строить сечение фигуры F секущей плоскостью α методом следов удобно в тех случаях, когда секущая плоскость задана тремя точками, ей принадлежащими, или прямой и не принадлежащей ей точкой, или двумя пересекающимися прямыми, или двумя параллельными прямыми. Во всех случаях легко взять три точки М, N, К, принадлежащие плоскости α, и решение проводить по указанной схеме.

7. — искомое сечение.

5. — искомое сечение.

При объяснении шагов построения можно использовать понятие гомологии или факты стереометрии, опираясь на наглядное представление о данных в условии задачи фигурах. Например, в последнем примере комментарии могут быть следующими.

1. То, что дано, считается построенным.

4. Находим прямую s пересечения плоскости основания и секущей плоскости, используя известные точки М, D , Е в секущей плоскости.

5. Очевиден шаг построения.

Заключение

Проведя исследование построения сечения методом следов, я установила, что метод следов легко объясним, нагляден, но не всегда удобен в практике построения сечений многогранников, так как расположение точек Х и У следа s может быть за рамками чертежа, прямые, определяющие точку Х (или Y ) могут быть параллельны. В тех случаях, когда применение метода следа затруднено, применяют метод внутреннего проецирования или так называемый метод вспомогательных сечений. Изучив параллельное проецирование, я научилась легко и быстро производить различные построения на плоскости. Эти навыки и умения помогли мне при изучении предметов школьного курса, таких как геометрия и черчение, а также при прохождении учебы на художественном отделении Динской школы искусств.

Литература

5. Начертательная геометрия- С. А. Фролов. «Просвещение», 2016. с. 137

Источник

§ 4. Параллельное и центральное проектирования

4.1 Определение и основные свойства параллельного проектирования

Параллельным проектированием пользуются, например, при изображении на плоскости (скажем, на бумаге) фигур, расположенных в пространстве. Определяется оно так. Пусть даны плоскость а и пересекающая её прямая а. Возьмём в пространстве произвольную точку X. В том случае, когда точка X не лежит на прямой а, через X проводим прямую а’, параллельную прямой а (рис. 42). Прямая а’ пересекает плоскость а в некоторой точке X’.

Эта точка называется параллельной проекцией (на плоскость а) точки X при проектировании в направлении прямой а. Если же точка X лежит на прямой а, то её параллельной проекцией X’ называется точка, в которой а пересекает а.

О прямой а говорят, что она задаёт направление проектирования. При замене прямой а любой другой параллельной ей прямой направление проектирования не изменится (поскольку две прямые, параллельные третьей прямой, параллельны).

Проекцией фигуры F называется фигура F’, состоящая из проекций всех точек фигуры F. Параллельную проекцию реальной фигуры представляет, например, её тень, падающая на плоскую поверхность при солнечном освещении, поскольку солнечные лучи можно считать параллельными (рис. 43). Перед вами картина И. И. Шишкина «Сосны, освещённые солнцем». Так, глядя на свою тень на земле, вы видите свою параллельную проекцию.

Выполняя параллельное проектирование, мы каждой точке фигуры F сопоставляли некоторую точку на плоскости а, т. е. выполняли некоторое преобразование фигуры F в фигуру F’. Напомним, что вообще преобразование некоторой фигуры F состоит в том, что каждой её точке X сопоставляется некоторая точка X’ (рис. 44). Все точки X’ образуют некоторую фигуру F’, и говорят, что фигура F преобразуется в фигуру F’. Говорят также, что точка X’ является образом точки Х, а фигура F’ — образом фигуры F для данного преобразования. Мы будем рассматривать различные преобразования фигур — проектирования, симметрии, движения, подобия.

Мы уже пользуемся параллельным проектированием при изображении пространственных фигур на плоскости и опираемся на его свойства для изображения отрезков и прямых, не параллельных направлению проектирования. Сформулируем и докажем их.

Свойство 1. Проекцией прямой является прямая, а проекцией отрезка — отрезок.

Свойство 2. Проекции параллельных прямых параллельны или совпадают.

Свойство 3. Отношение проекций отрезков, лежащих на одной прямой, равно отношению самих отрезков.

Доказательство. Пусть α — плоскость проекции и прямая а задаёт направление проектирования.

1. Рассмотрим какую-либо прямую Ь, не параллельную прямой а. Так как а можно заменить любой параллельной ей прямой, то можно считать, что а пересекает Ь. Тогда через прямые а и b проходит плоскость β. Она пересекает плоскость α по некоторой прямой b’. Прямая Ь’ и будет проекцией прямой b (рис. 45).

В самом деле, проекцией каждой точки X ∈ Ь будет некоторая точка X’ ∈ Ь’ и каждая точка Y’ ∈ b’ является проекцией некоторой точки Y ∈ b. Это так, поскольку все проектирующие прямые, пересекающие прямую b (прямую b’), находятся в плоскости β, а значит, пересекают прямую b'(прямую Ь).

Любой отрезок АВ, лежащий на прямой b, проектируется в отрезок А’В’ прямой Ь’ где А’ и В’ — проекции точек А и В. Действительно, проектирующая прямая а, проходящая через любую внутреннюю точку X отрезка АВ, идёт между проектирующими прямыми, проходящими через А и В. Поэтому и точка X’ лежит между А’ и В’, т. е. на отрезке А’В’. Когда X пробегает отрезок АВ, точка X’ пробегает отрезок А’В’.

3. Рассмотрим два отрезка АВ и CD у лежащие на прямой Ь. Проекции А’В’ и C’D’ отрезков АВ и CD лежат на прямой b’ (рис. 46, б). Проектирующие прямые, проходящие через точки А, B, С, D, параллельны прямой а и, стало быть, параллельны друг другу. Кроме того, они все лежат в плоскости β. По известной теореме планиметрии параллельные прямые отсекают на двух прямых пропорциональные отрезки. Значит, АВ : CD = А’В’: C’D’.

Все три свойства доказаны.

4.2 Изображение разных фигур в параллельной проекции

Рисунки, иллюстрирующие предложения стереометрии и представляющие фигуры в пространстве, делают обычно в параллельной проекции. Точнее, за изображение фигуры принимается фигура, подобная какой-либо её параллельной проекции. Фигура, подобная параллельной проекции фигуры, очевидно, обладает теми же свойствами, которые доказаны в п. 4.1. Поэтому, делая рисунки, надо следить за тем, чтобы выполнялись эти свойства.

Рассмотрим изображения некоторых фигур. Случай, когда фигура лежит в плоскости, заполненной проектирующими прямыми, и, следовательно, проектируется в фигуру, лежащую на прямой, исключаем.

1. Треугольник. Каждый треугольник можно параллельно спроектировать так, что в проекции получится треугольник любого вида, т. е. подобный любому заданному треугольнику.

Действительно, пусть даны два треугольника АBС и А₁В₁С₁. Проведём через прямую АВ плоскость а, пересекающую плоскость треугольника АBС. На ней построим треугольник АBС’, подобный треугольнику АХВгС19 прилегающий к треугольнику АBС по стороне АВ (рис. 46, в). Тогда при проектировании на плоскость α параллельно прямой СС треугольник АБС спроектируется на треугольник ABC’ так, что его проекция будет подобна треугольнику А₁В₁С₁. В частности, всякий треугольник можно спроектировать так, чтобы получился равносторонний треугольник.

2. Параллелограмм. Изображением параллелограмма может служить любой параллелограмм. (Почему? Какая связь с изображением треугольника?)

3. Изображение плоской фигуры. Для изображения плоской фигуры можно поступить так. В данной фигуре выделяют какие-нибудь три точки, не лежащие на одной прямой, и строят треугольник с вершинами в этих точках; обозначим их А, В, С (рис. 47). Строят изображение треугольника ABC в виде произвольного треугольника А’В’С’. После того как построено это изображение, никакого произвола в изображении фигуры быть не может. Покажем это.

Пусть изображением треугольника ABC служит треугольник А’В’С’ (рис. 48). Пусть точка X лежит в плоскости ABC и луч СХ пересекает отрезок АВ во внутренней его точке D. Проекция точки D — точка D’ — лежит на отрезке А’В’ (откуда это следует?), и .

Следовательно, точку D’ на отрезке А’В’ можно построить на рисунке (как?). Далее проводим луч C’D’ и на нём отмечаем такую точку X’, что (объясните, как это сделать). Мы построили на рисунке проекцию данной точки X плоскости ABC. (Точка X может располагаться и по-иному относительно треугольника ABC, но и тогда построение будет аналогичным.)

4. Тетраэдр. Изображать тетраэдр можно любым по форме четырёхугольником с диагоналями. Эту трудную теорему доказали в середине XIX века два немецких геометра Карл Польке и Герман Шварц. Чаще всего тетраэдр рисуют так, как он изображён на рисунке 49, а (штриховой линией выделяется невидимое ребро). Но можно его изобразить и так, как на рисунке 49, б: это правильно, но менее наглядно.

5. Изображение пространственной фигуры. При изображении пространственной фигуры роль изображения тетраэдра аналогична роли изображения треугольника при изображении плоской фигуры. Изображая пространственную фигуру, в ней выделяют сначала четыре точки, не лежащие в одной плоскости, т. е. вершины некоторого тетраэдра, и строят его изображение. После того как построено изображение этого тетраэдра, никакого произвола в изображении точек данной фигуры быть не должно. Покажем это.

Пусть ABCD — выделенный тетраэдр, а A’B’C’D’ — его изображение. Возьмём точку X данной фигуры, и пусть луч СХ пересекает плоскость ABD в точке К внутри треугольника ABD (рис. 50). Изображение точки К — точка К’ лежит внутри треугольника A’B’D’ (откуда это следует?), причём она может быть построена (мы показали это в примере 3). Но тогда изображение X’ точки X лежит на луче С’К’ причём .

Точка X может располагаться по-иному относительно тетраэдра, но и тогда рассуждение будет аналогичным.

Вообще же, как вы уже поняли, глядя, например, на рисунок 29, далеко не каждому рисунку соответствует пространственная фигура, которую изображает данный рисунок. Завершим этот пункт тремя известными парадоксами, основанными на неверном изображении пространственных объектов (рис. 51—52).

Какие из правил изображения в них нарушены?

4.3 Центральное проектирование

В курсах геометрии для изображения на плоскости чертежа или рисунка пространственных фигур применяется параллельное проектирование. Но в живописи, архитектуре и при фотографировании используется другой вид проектирования на плоскость — центральное проектирование. Его свойства сложнее свойств параллельного проектирования, но оно даёт большую наглядность изображению.

Центральное проектирование на плоскость определяется так. В пространстве фиксируется некоторая точка О (центр проектирования) и плоскость α (плоскость проекций), не проходящая через О. Через любую точку X проводится прямая ОХ — проектирующая прямая.

Если прямая ОХ пересекает α, то точка X’ их пересечения называется центральной проекцией точки X на плоскость α из точки О (рис. 53).

Из данного определения следует, что не каждая точка пространства проектируется из центра О в некоторую точку плоскости α: если прямая ОХ параллельна α, то точки X’ нет (в то время как при параллельном проектировании все точки имеют проекции).

Центральное проектирование не сохраняет параллельности прямых (рис. 54; вспомните, что, когда мы смотрим вдаль на параллельные рельсы, нам кажется, что они пересекаются на линии горизонта).

Легко понять, что и отношение длин отрезков, лежащих на одной прямой, не параллельной плоскости проекций, не сохраняется при центральном проектировании (рис. 55).

Примерами фигур, получающихся друг из друга при центральном проектировании, являются сечения одного конуса разными плоскостями (см. рис. 162, б, 164, а, 165, в, 167, 168).

Изображение пространственных фигур на плоскости с помощью центрального проектирования называется перспективой. Теория перспективы возникла из потребностей архитектуры и живописи. Некоторые законы перспективы были известны ещё древнегреческим геометрам: Аполлонию Пергскому (III в. до н.э.), Meнелаю (I в.), Паппу (III в.).

Теорией перспективы занимались крупнейшие художники эпохи Возрождения — Леонардо да Винчи (1452—1519) и Альбрехт Дюрер (1471—1528).

В дальнейшем теория перспективы развилась в один из разделов современной геометрии — проективную геометрию — учение о свойствах фигур, сохраняющихся при центральном проектировании.

Основы её заложил французский математик Жерар Дезарг (1591—1661). Он ввёл так называемые бесконечно удалённые элементы. Дезарг считал, что все параллельные друг другу прямые пересекаются в одной бесконечно удалённой точке, а все бесконечно удалённые точки одной плоскости лежат на одной бесконечно удалённой прямой.

Окончательно проективная геометрия оформилась как самостоятельная область геометрии в работах французского геометра Жана Виктора Понселе (1788—1867). (Ж.-В. Понселе был офицером наполеоновской армии и свой основной труд «Трактат о проективных свойствах фигур», вышедший в 1822 г., написал в 1813—1814 гг. в Саратове, находясь в русском плену.)

Источник