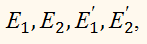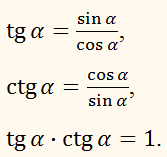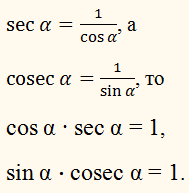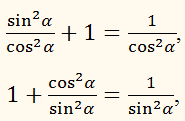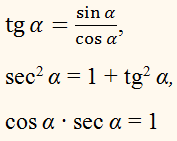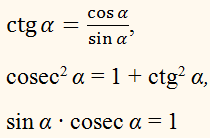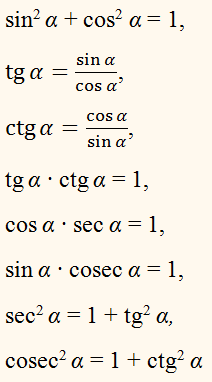что такое основное тригонометрическое тождество определение

1.2.4 Основные тригонометрические тождества

Видеоурок: Тригонометрические тождества

Лекция: Основные тригонометрические тождества

Итак, напомним, что при рассмотрении тригонометрических функций, мы используем единичную окружность, с радиусом, равным единице.

Рассмотрим произвольный прямоугольный треугольник, полученный в результате движения радиус-вектора на некоторый угол.

К прямоугольному треугольнику применима теорема Пифагора, в соответствии с которой квадрат гипотенузы будет равен сумме квадратов остальных сторон треугольника. Так как мы знаем, что синусу соответствует значение ординаты на плоскости, то есть величина противолежащего катета, а косинусу значение абсциссы (прилежащего катета). Так же нам известно, что гипотенуза треугольника является радиусом окружности, длина которого равна единицы, то теорему Пифагора можем получить в следующем виде:

Остальные тригонометрические тождества мы можем получить, зная определение тангенса и котангенса.

Давайте перемножим первое и второе уравнение и посмотрим, что получилось. В результате данного математического действия получим, что произведение тангенса на котангенс равно единице:

А теперь давайте возьмем первое основное тождество и почленно разделим все на cos 2 α или на sin 2 α. В результате этого получим:

Первое тождество справедливо для всех углов. Остальные же используются исключительно при углах, синус и косинус которых не равен 0.

Источник

Основные тригонометрические формулы и тождества sin, cos, tg, ctg

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

На основе формул сложения выводятся тригонометрические формулы кратного угла.

Формулы кратного угла: двойного, тройного и т.д.

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

Формулы понижения степени

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

Произведение тригонометрических функций

Формулы произведения тригонометрических функций

Универсальная тригонометрическая подстановка

Универсальная тригонометрическая подстановка

Источник

Уроки математики и физики для школьников и родителей

среда, 23 января 2019 г.

Урок 11. Основные тригонометрические тождества

Формулы тригонометрии – это соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом.

Для преобразования тригонометрических выражений используют свойства тригонометрических функций и формулы тригонометрии.

Соотношения между тригонометрическими функциями одного и того же угла.

а длина отрезка ОМ равна единице:

Из прямоугольного треугольника ОРМ имеем:

sin 2 α + cos 2 α = 1.

Если точка М совпадает с одной из точек

а следовательно, и формула

sin 2 α + cos 2 α = 1

верны и в этом случае.

sin 2 α + cos 2 α = 1

sin 2 α + cos 2 α = 1

где k – любое целое число.

верна при всех значениях α кроме тех, при которых не определена хотя бы одна из функций tg α и ctg α, то есть при всех значениях α кроме

где k – любое целое число.

cosec 2 α = 1 + ctg 2 α

позволяют на чертеже

sin 2 α + cos 2 α = 1,

получается из соответствующего прямоугольника на основании теоремы Пифагора. Остальные же формулы получаются из рассмотрения трёх пар подобных треугольников. Поэтому, чтобы написать ту или другую из восьми формул, достаточно воспроизвести следующий чертёж.

Источник

Основное тригонометрическое тождество

Основным тригонометрическим тождеством в русскоязычных учебниках математики называют соотношение , выполняющееся для произвольного значения .

Основное тригонометрическое тождество представляет собой запись теоремы Пифагора для треугольника в тригонометрическом круге; длины катетов этого треугольника по модулю равны соответствующим синусу и косинусу, а гипотенуза, будучи радиусом тригонометрического круга, равна единице.

В учебниках математики, написанных на языках, отличных от русского, соответствующее соотношение называют «тригонометрическим тождеством Пифагора» (см. Pythagorean trigonometric identity в английской Википедии) или просто теоремой Пифагора.

См. также

Смотреть что такое «Основное тригонометрическое тождество» в других словарях:

Основное — название нескольких населённых пунктов: Основное хутор в Железногорском районе Курской области. Основное деревня в Черемисиновском районе Курской области. См. также Основное богословие Основное кинетическое уравнение Основное общество Основное… … Википедия

Теорема косинусов — Теорема косинусов теорема евклидовой геометрии, обобщающая теорему Пифагора: Для плоского тре … Википедия

Варахамихира — वराहमिहिर Дата рождения: 505 год(0505) Дата смерти: 587 год(0587) Научная сфера … Википедия

ОТТ — оперативно тактические требования Словарь: С. Фадеев. Словарь сокращений современного русского языка. С. Пб.: Политехника, 1997. 527 с. ОТТ общий таможенный тариф ОТТ оперативно тактический тренажёр Словарь: Словарь сокращений и аббревиатур армии … Словарь сокращений и аббревиатур

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ — раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях. ЭЛЕКТРОСТАТИКА В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между… … Энциклопедия Кольера

Эллиптические координаты — Эллиптическая система координат Эллиптические координаты двумерная ортогональная система координат … Википедия

Источник

Как доказать тригонометрическое тождество?

Тождество – равенство, верное при любых значениях переменных, кроме тех при которых какая-либо часть тождества не имеет смысла.

А вот выражение \(\frac=x\) является тождеством только при условии \(x≠0\) (иначе левая часть не существует).

Как доказывать тождество?

Рецепт до одури прост:

Чтобы доказать тождество нужно доказать, что его правая и левая части равны, т.е. свести его к виду «выражение» = «такое же выражение».

Для того, чтоб это сделать можно:

Пример. Доказать тригонометрическое тождество \(\sin⁡2x=2\sin⁡x\cdot \cos\)
Решение:

\(\sin⁡2x=2 \sin⁡x\cdot \cos \)

Будем преобразовывать левую часть.
Представим \(2x\) как \(x+x\)…

Левая часть равна правой – тождество доказано.

Будем преобразовывать только левую часть. Приведем слагаемые к общему знаменателю.

Применим в числителе вездесущие основное тригонометрическое тождество: \(\sin^2⁡+\cos^2<⁡x>=1\).

Левая часть равна правой, тождество доказано.

Левая часть равна правой, тождество доказано.

Сократим дробь на \(\cos<⁡t>+\sin<⁡t>\).

Почленно разделим дробь, превратив ее в две отдельные дроби.

Левая часть равна правой, тождество доказано.

Как видите, все довольно несложно, но надо знать все формулы и свойства.

Как доказать основное тригонометрическое тождество

Два простых способа вывести формулу \(\sin^2x+\cos^2x=1\). Нужно знать только теорему Пифагора и определение синуса и косинуса.

Ответы на часто задаваемые вопросы:

Источник