что такое основание прямоугольника

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые.

Частным случаем прямоугольника является квадрат.

Свойства прямоугольника

1. Так как прямоугольник – это параллелограмм, то все свойства параллелограмма верны и для прямоугольника.

Помимо этого:

2. Стороны прямоугольника являются его высотами.

3. Диагонали прямоугольника равны.

4. Квадрат диагонали прямоугольника равен сумме квадратов двух его соседних сторон.

5. Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.

Признаки параллелограмма

Параллелограмм является прямоугольником, если выполняется любое из условий:

1. Диагонали параллелограмма равны.

2. Квадрат диагонали параллелограмма равен сумме квадратов соседних сторон.

3. Все углы параллелограмма равны.

Площадь прямоугольника

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Прямоугольник, свойства, признаки и формулы

Прямоугольник, свойства, признаки и формулы.

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник (понятие, определение):

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник – это четырехугольник, у которого каждый угол является прямым.

Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник

В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.

Свойства прямоугольника:

1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник

2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник

3. Стороны прямоугольника являются его высотами.

4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник

5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник

6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник

Рис. 7. Прямоугольник

8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).

Рис. 8. Прямоугольник

9. Диагонали прямоугольника делятся точкой пересечения пополам.

10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

АС и BD – диаметр описанной окружности и диагональ прямоугольника

11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.

12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.

Признаки прямоугольника:

– если диагонали параллелограмма равны, то он является прямоугольником;

– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;

– если углы параллелограмма равны, то он является прямоугольником.

Формулы прямоугольника:

Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.

Формула стороны прямоугольника (длины и ширины прямоугольника):

,

,

,

.

Формула диагонали прямоугольника:

,

Формулы периметра прямоугольника:

Формулы площади прямоугольника:

Формула радиуса окружности, описанной вокруг прямоугольника:

.

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Мировая экономика

Справочники

Востребованные технологии

Поиск технологий

О чём данный сайт?

Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.

Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.

Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!

Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.

О Второй индустриализации

Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.

Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.

Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.

Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.

Источник

Что такое прямоугольник: определение, свойства, признаки, формулы

В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.

Определение прямоугольника

Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).

∠ABC = ∠BCD = ∠BAD = ADC = 90°

Прямоугольник состоит из:

Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.

Примечание: Прямоугольник является разновидностью параллелограмма.

Свойства прямоугольника

Свойство 1

Противоположные стороны прямоугольника попарно параллельны и равны.

Свойство 2

Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.

Свойство 3

Если соединить середины сторон прямоугольника, то получится ромб.

Свойство 4

Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.

d 2 = a 2 + b 2

Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.

Свойство 5

Диагонали прямоугольника равны, и в точке пересечения делятся пополам.

Свойство 6

Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.

Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.

Признаки прямоугольника

Параллелограмм является прямоугольником, если верно одно из следующих утверждений:

Формулы

1. Площадь прямоугольника (S):

2. Периметр прямоугольника (P):

Источник

Площадь прямоугольника 91 см в квадрате а его высота 7 см Определите основания прямоугольника

Ответ или решение 2

Согласно условию поставленной задачи, площадь прямоугольника равна 91 сантиметру в квадрате, причем высота прямоугольника равна 7 сантиметров. Необходимо определить основание прямоугольника.

Рассмотрим некоторые свойства прямоугольника

Найдем основание данного искомого прямоугольника

Пусть основание прямоугольника из поставленной задачи равно Х сантиметров.

Поэтому, можно составить одно уравнение с одной неизвестной и решить его. Получается: Х * 7 = 91, а, следовательно, Х = 91 : 7 = 13 см.

Ответ: основание данного прямоугольника равно 13 сантиметров.

Прямоугольником называется четырех угольник, у которого все углы прямые, то есть равны 90 градусов. У прямоугольника противоположные стороны равны и параллельны. Площадь прямоугольника равна произведению его длины и ширины. С условия задачи известна площадь прямоугольника, а так же известна величина ширины прямоугольника. Ответим на вопрос задачи.

1). Определим основание прямоугольника, то есть его длину.

91 / 7 = 13 сантиметров.

Ответ: Длина прямоугольника равна тринадцать сантиметров.

Источник

Прямоугольный параллелепипед. Что это такое?

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

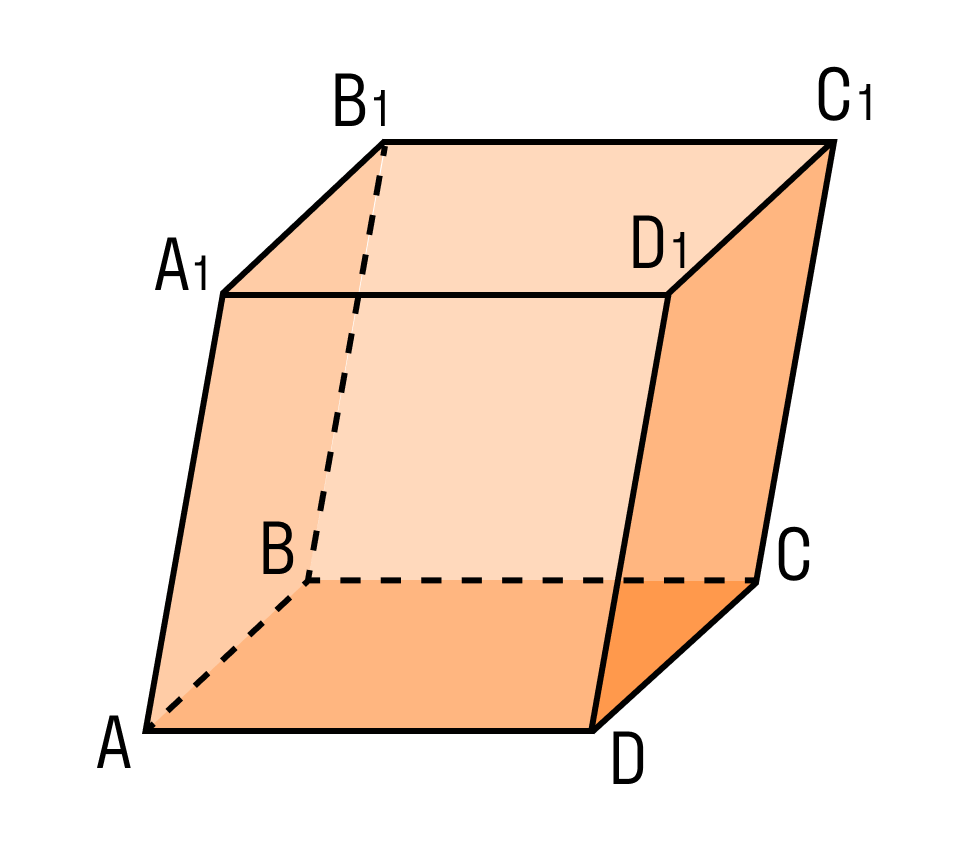
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Формулы прямоугольного параллелепипеда:

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

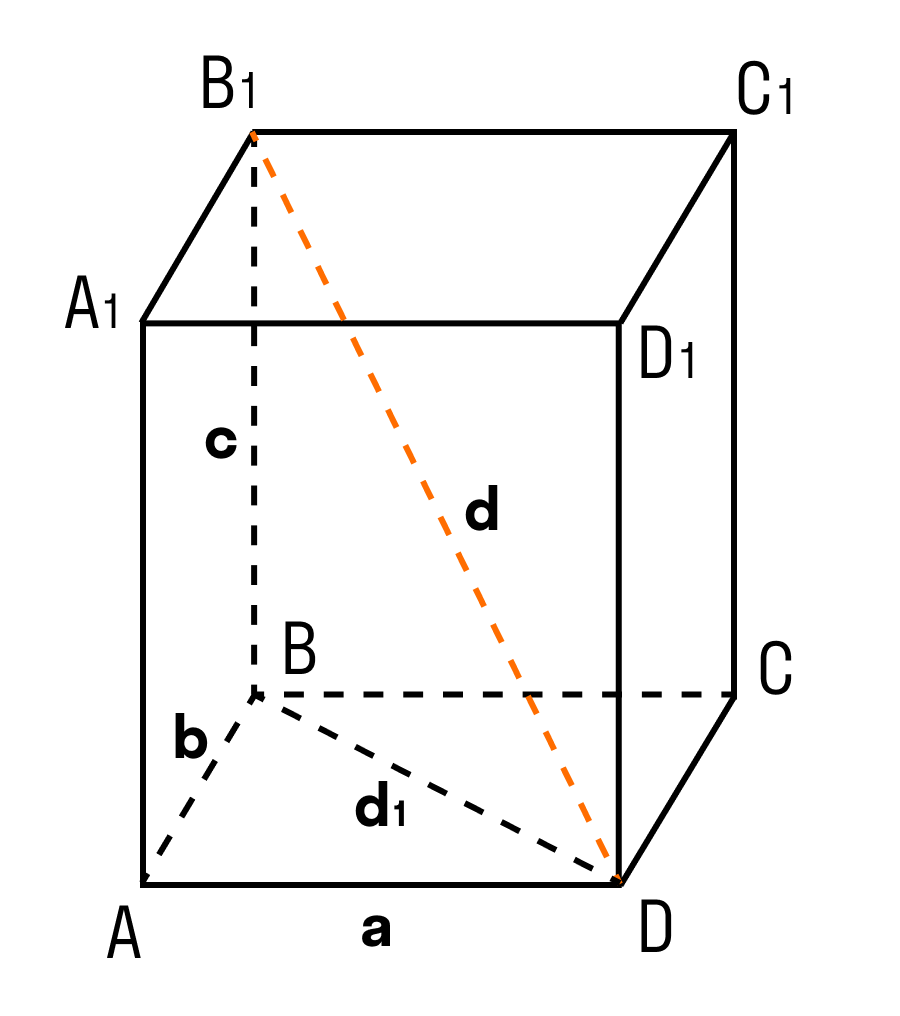
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

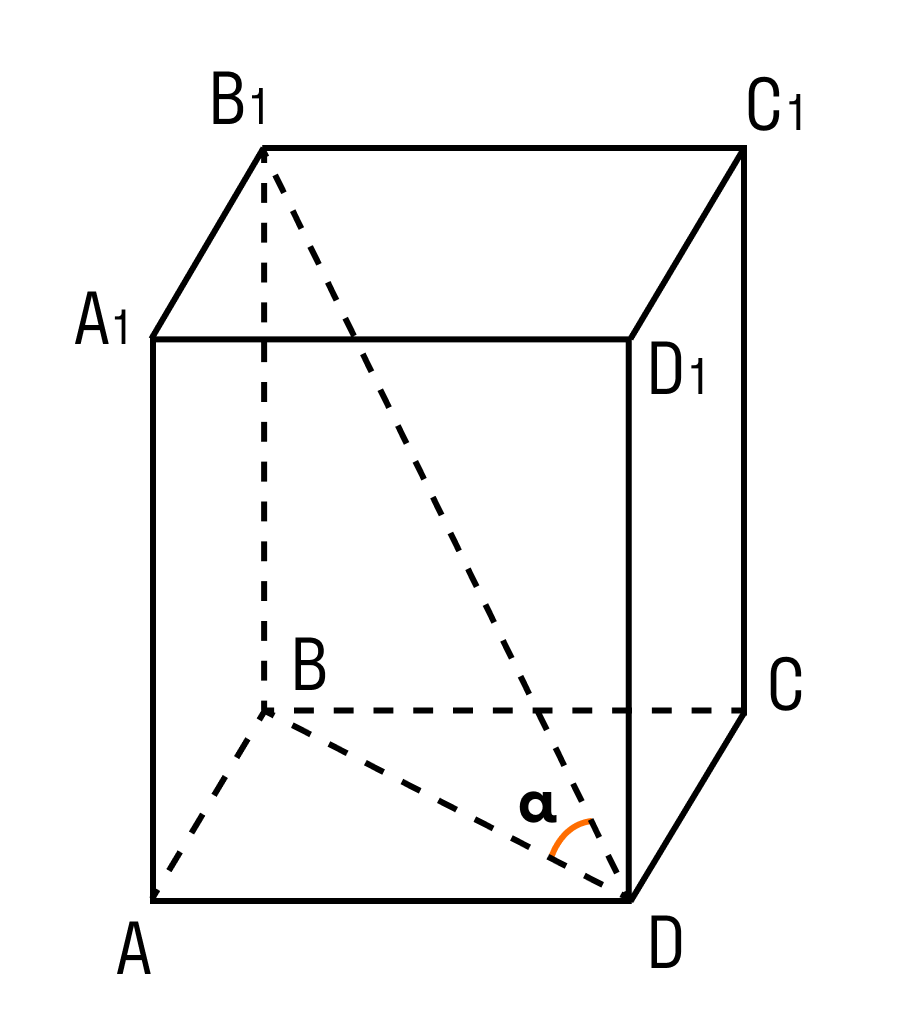
Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

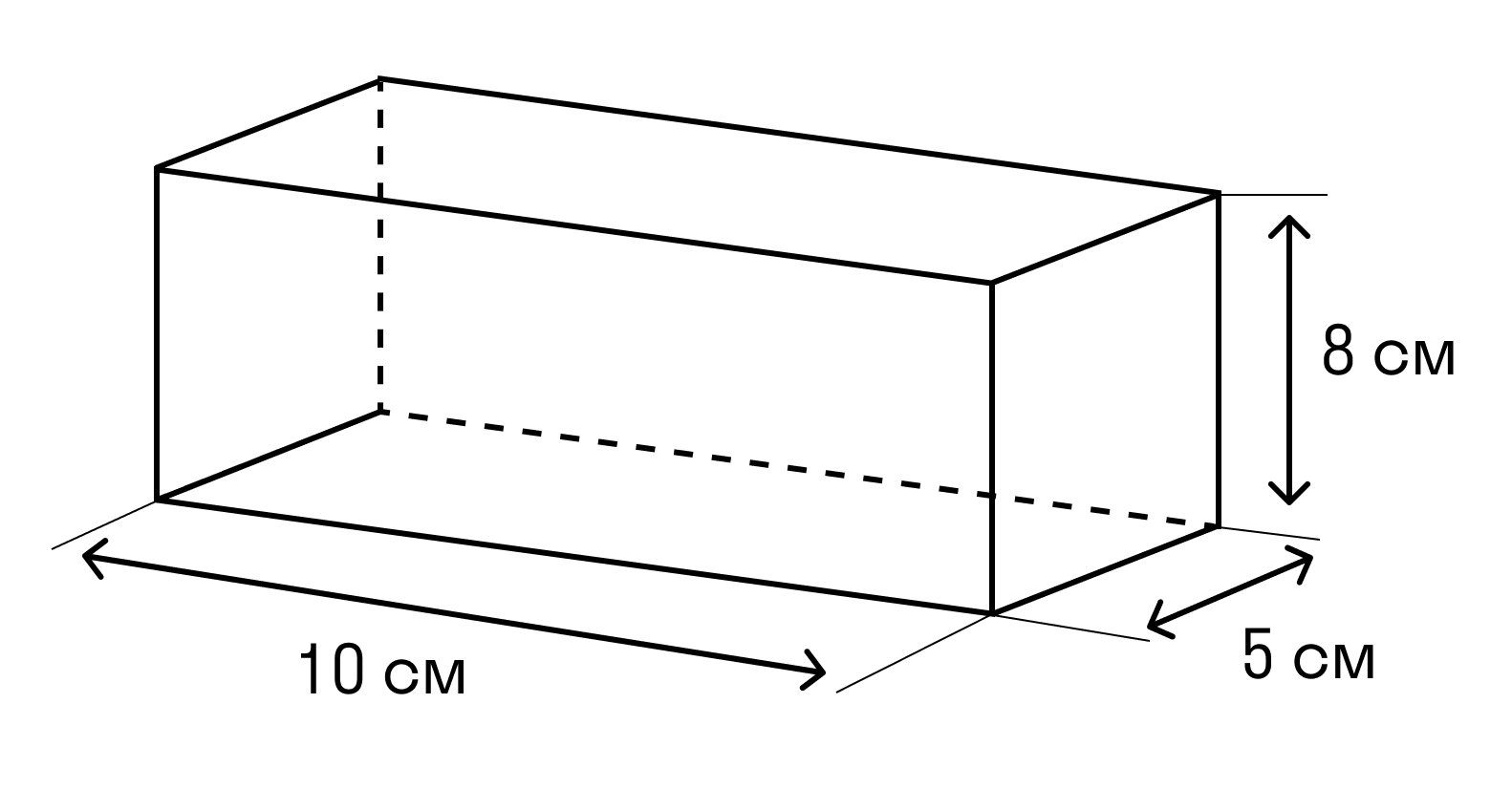
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

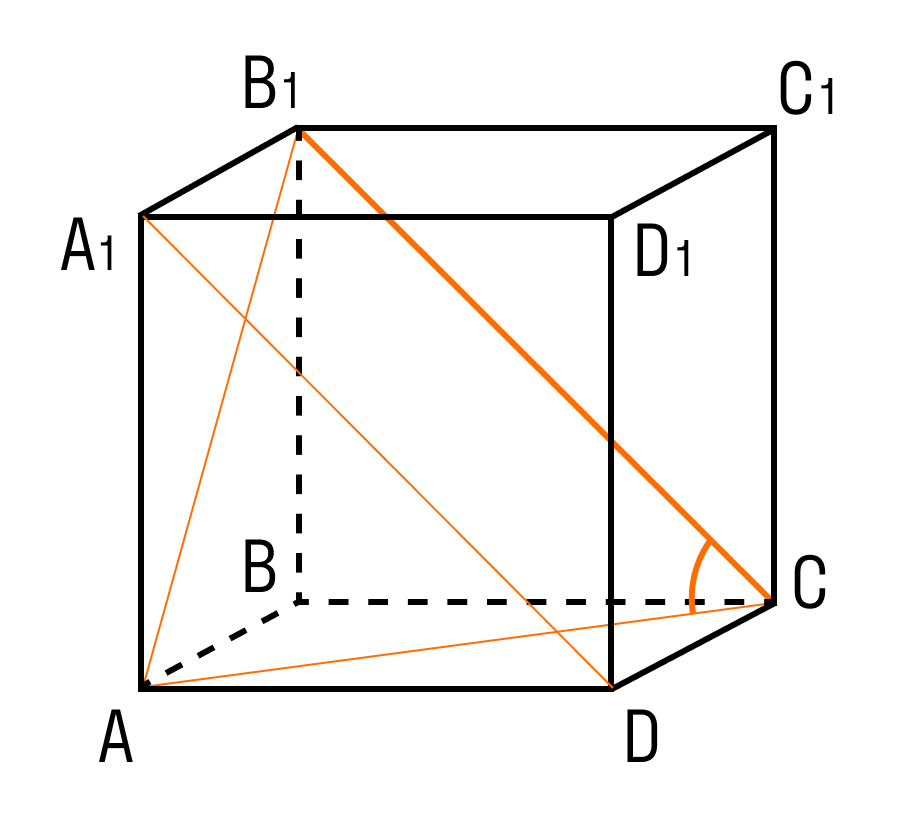
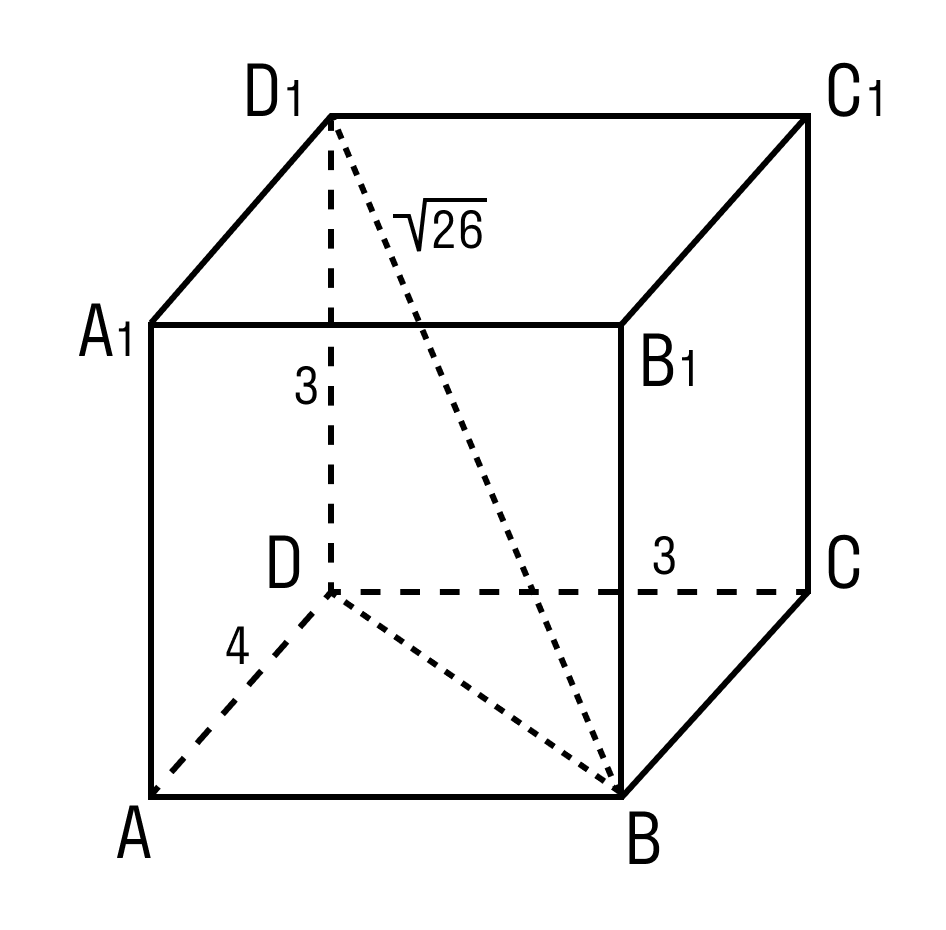
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.

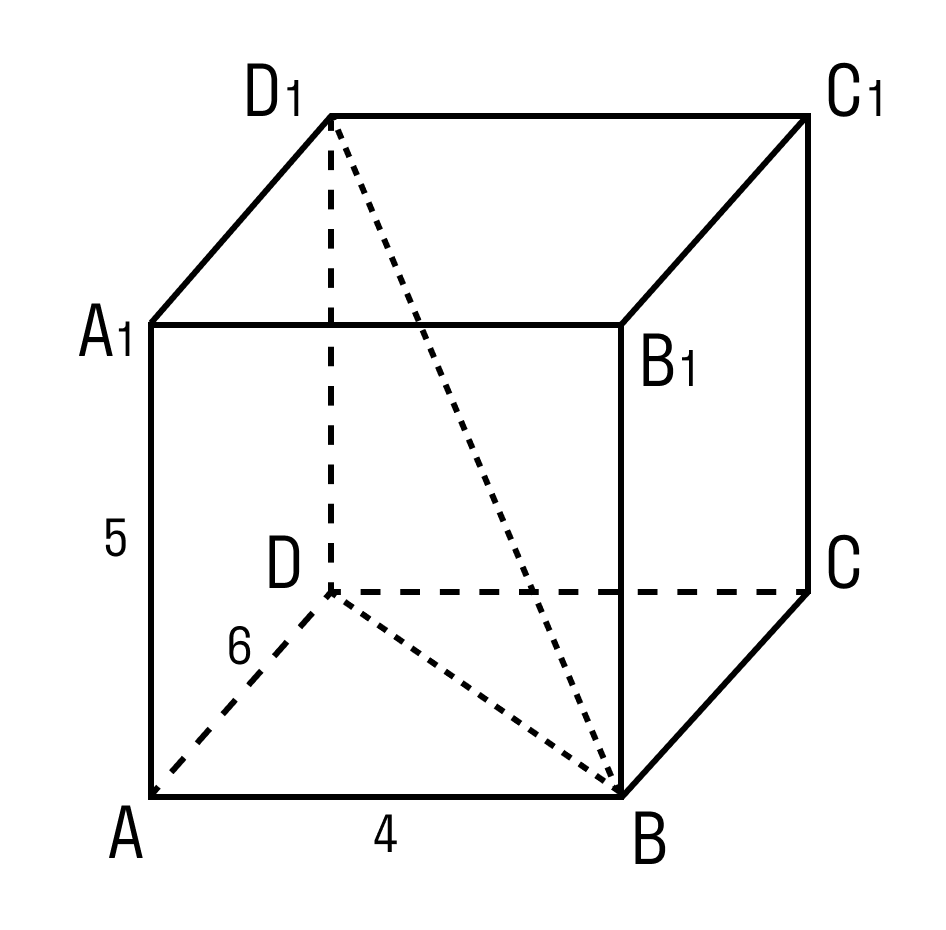
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Источник