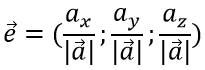что такое орт в математике

Единичный вектор

Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.

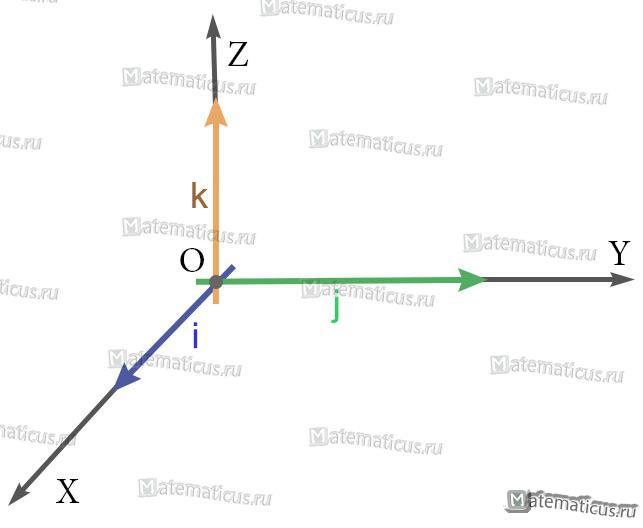
i — единичный вектор оси абсцисс;

j — единичный вектор оси ординат;

k — единичный вектор оси аппликат.

i⊥j⊥k, i=j=k=1

В прямоугольной системе координат в пространстве координаты векторов равны:

i(1;0;0), j(0;1;0), k(0;0;1)

Единичные векторы являются некомпланарными.

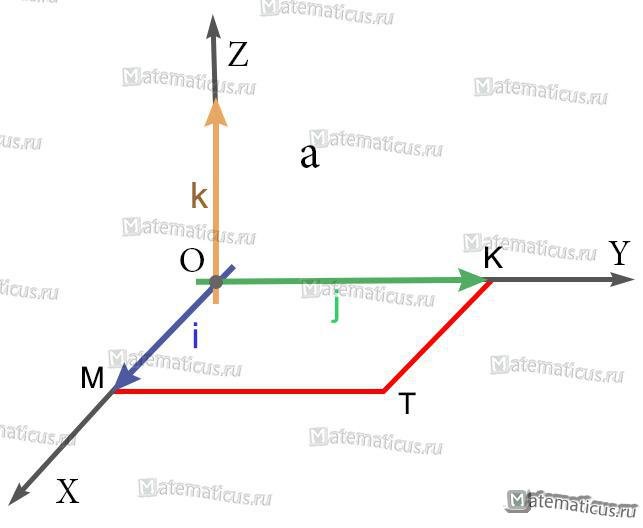
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.

a=xi+уj+zk

где x, y, z — координаты вектора проекции на соответствующие координатные оси.

Эта формула называется разложением вектора по ортам координатных осей.

Единичный вектор определяется по формуле:

Требуется найти длину (модуль) и единичный вектор e направления вектора а

Находим длину вектора a

затем вычисляем единичный вектор e

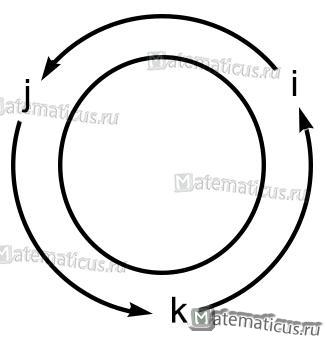
Векторное произведения единичных векторов

На основании схемы получаем таблицу векторного произведения единичных векторов

Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.

iхj=k

Пример 2
Найти векторное произведение jхi.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.7 / 5. Количество оценок: 3

Источник

Орт (матем.)

Смотреть что такое «Орт (матем.)» в других словарях:

ОРТ — а; м. [нем. Ort] 1. Горн. Горизонтальная подземная горная выработка, не имеющая непосредственного выхода на поверхность. 2. Матем. Вектор, длина которого равна единице. * * * ОРТ (Общественное российское телевидение), телекомпания (ЗАО; 51% акций … Энциклопедический словарь

орт — а; м. [нем. Ort] 1. Горн. Горизонтальная подземная горная выработка, не имеющая непосредственного выхода на поверхность. 2. Матем. Вектор, длина которого равна единице. * * * орт I (от греч. orthós прямой), то же, что единичный вектор. II (нем.… … Энциклопедический словарь

Орт — I (от греч. orthós прямой) (матем.), то же, что Единичный вектор. II (нем. Ort, буквально место) в горном деле, горизонтальная подземная горная выработка, не имеющая непосредственного выхода на поверхность и проведённая в сторону… … Большая советская энциклопедия

орт — а; м. (нем. Ort) 1) горн. Горизонтальная подземная горная выработка, не имеющая непосредственного выхода на поверхность. 2) матем. Вектор, длина которого равна единице … Словарь многих выражений

Брушлинский, Константин Владимирович — Брушлинский Константин Владимирович … Википедия

ТЕЛЕВИДЕНИЕ — область науки, техники и культуры, связанная с передачей на расстояние изображений объектов и звукового сопровождения (речи, музыки и др.). при помощи радиосигналов Чаще всего под назв «телевидение» понимается формирование и трансляция… … Российская педагогическая энциклопедия

вектор — ▲ отрезок ↑ направленный вектор направленный отрезок, элемент линейного пространства, векторного поля (матем). векторный (# произведение). орт. равнодействующая. градиент. | дивергенция. годограф. | индикатриса. репер. базис (ортонормированный #) … Идеографический словарь русского языка

Источник

Что такое орт в математике

Получите бесплатный курс по основам математики. Эти знания необходимы для решения задач по физике.

Векторная алгебра с нуля!

Получите бесплатный курс по Векторной алгебре. Он необходим для решения задач по физике.

Книги по изучению физики и для подготовки к ЕГЭ

Единичные векторы. Орты. Декартова система координат

Очевидно, а = а·а_е (а — модуль вектора а). Это следует из правила, по которому выполняется операция умножения скаляра на вектор.

Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат.

Дело в том, что, например, в механике при изучении движения тел прямоугольная система координат используется очень часто. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i, j, k.

Но нередко, когда объект движется по какой-то криволинейной траектории (например, по окружности) бывает удобнее рассматривать механические процессы в системе координат, движущейся с этим объектом. Именно для такой движущейся системы координат и используются другие названия осей и их ортов. Просто так принято. В этом случае ось X направляют по касательной к траектории в той ее точке, в которой в данный момент этот объект находится. И тогда эту ось называют уже не осью X, а касательной осью, а ее орт обозначают уже не i, а τ. Ось Y направляют по радиусу кривизны траектории (в случае движения по окружности – к центру окружности). А поскольку радиус перпендикулярен касательной, то ось называют осью нормали (перпендикуляр и нормаль – это одно и то же). Орт этой оси обозначают уже не j, а n. Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это – бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.

Книги по изучению физики и для подготовки к ЕГЭ
Эти книги должен иметь каждый старшеклассник, абитуриент и студент!

Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).

Источник

Что такое орт в математике

, единичный вектор,- вектор, длина к-рого равна единице выбранного масштаба.

Смотреть что такое «ОРТ» в других словарях:

орт — орт, а … Русский орфографический словарь

Орт — Орт: В Викисловаре есть статья «орт» Орф, или Орт двуглавый пёс, порождение Тифона и Ехидны, брат Цербера. Орт … Википедия

Орт — горизонтальная подземная горная выработка, проходимая в пределах залежи полезного ископаемого вкрест ее простирания. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

ОРТ — а; м. [нем. Ort] 1. Горн. Горизонтальная подземная горная выработка, не имеющая непосредственного выхода на поверхность. 2. Матем. Вектор, длина которого равна единице. * * * ОРТ (Общественное российское телевидение), телекомпания (ЗАО; 51% акций … Энциклопедический словарь

орт — а; м. [нем. Ort] 1. Горн. Горизонтальная подземная горная выработка, не имеющая непосредственного выхода на поверхность. 2. Матем. Вектор, длина которого равна единице. * * * орт I (от греч. orthós прямой), то же, что единичный вектор. II (нем.… … Энциклопедический словарь

орт — выработка, квершлаг, сбойка, вектор Словарь русских синонимов. орт сущ., кол во синонимов: 8 • вектор (5) • … Словарь синонимов

орт — 1 іменник чоловічого роду вектор орт 2 іменник чоловічого роду штольня … Орфографічний словник української мови

ОРТ — (от греч. orthos прямой) то же, что единичный вектор … Большой Энциклопедический словарь

ОРТ — (нем. Ort) горная горизонтальная подземная выработка, проведенная в толще полезного ископаемого под углом к простиранию месторождения и не имеющая непосредственного выхода на земную поверхность … Большой Энциклопедический словарь

Орт — нескл. ср. Общественное российское телевидение. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

Источник

Что такое орт в математике

Сформулируем ряд базовых определений.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

Геометрически два вектора складываются по двум правилам:

а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

При λ>0 – вектор сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l ), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Отсюда следует условие перпендикулярности ненулевых векторов и :

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

Угол φ между и находим по формуле (2.29), то есть

– перпендикулярен векторам и ;

– векторы образуют правую тройку (рис. 2.15).

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

— перпендикулярен плоскости, проходящей через точки O , A , B ;

Следовательно, момент силы относительно точки O представляет собой векторное произведение

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

Объем треугольной пирамиды, построенной на этих же векторах, равен

Решение. Найдем координаты векторов

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

получим выражение вектора через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

Базисом n – мерного пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Источник