что такое ординальные признаки
Что такое ординальные признаки
Непростой тест на общие знания: Пройдете его хотя бы на 7/10?
В чём ваш мозг крут
Cколько лет вашей душе?
Тест на смекалку, в котором вы вряд ли наберете 8 правильных ответов, если ваш IQ ниже среднего
Вы — настоящий интеллигент, если сможете закончить 10 крылатых фраз — ТЕСТ
Тест: Узнайте что говорит дата рождения о вашей Личности
Насколько у вас хорошая логика?
Тест Роршаха расскажет, что сейчас творится у вас в голове
Умеете ли вы готовить? Сложный кулинарный Блиц-тест ресторатора Ивана Шишкина
На какое животное вы похожи, когда злитесь?
Тест, который осилят лишь настоящие профи в мировой географии
Сумеешь угадать фильм с одного кадра?
Цветовой тест: попробуем отгадать ваш возраст всего за 9 вопросов
Проверьте свой интеллект
Только 4% людей способны пройти этот тест с вопросами различной направленности
Никто не может ответить больше чем на 7 из 10 вопросов в этом тесте на IQ
Тест на общие знания, который без ошибок проходят лишь единицы. А получится ли у вас?
Тест на интеллект: Если наберете 9/9, то уровень вашего IQ точно выше среднего
Вы очень интересный собеседник, если наберете в нашем тесте хотя бы 8/10 — ТЕСТ
Что вас ждет в старости?
Подписывайтесь на наши странички! Обязательно делитесь с друзьями! Впереди много новых интересных тестов! Ежедневные добавления! Страницы: Яндекс Дзен, ВКонтакте, Одноклассники, Facebook
Популярные тесты
Непростой тест на общие знания: Пройдете его хотя бы на 7/10?
В чём ваш мозг крут
Cколько лет вашей душе?
Тест на смекалку, в котором вы вряд ли наберете 8 правильных ответов, если ваш IQ ниже среднего
Вы — настоящий интеллигент, если сможете закончить 10 крылатых фраз — ТЕСТ
Тест: Узнайте что говорит дата рождения о вашей Личности
Насколько у вас хорошая логика?
Тест Роршаха расскажет, что сейчас творится у вас в голове
Умеете ли вы готовить? Сложный кулинарный Блиц-тест ресторатора Ивана Шишкина
На какое животное вы похожи, когда злитесь?
Тест, который осилят лишь настоящие профи в мировой географии
Сумеешь угадать фильм с одного кадра?
Цветовой тест: попробуем отгадать ваш возраст всего за 9 вопросов
Проверьте свой интеллект
Только 4% людей способны пройти этот тест с вопросами различной направленности
Никто не может ответить больше чем на 7 из 10 вопросов в этом тесте на IQ
Тест на общие знания, который без ошибок проходят лишь единицы. А получится ли у вас?
Тест на интеллект: Если наберете 9/9, то уровень вашего IQ точно выше среднего
Вы очень интересный собеседник, если наберете в нашем тесте хотя бы 8/10 — ТЕСТ
Что вас ждет в старости?
Преимущества
Можете встраивать тесты на Ваш сайт. Тест показывается нашем и других сайтах. Гибкие настройки результатов. Возможность поделиться тестом и результатами. Лавинообразный («вирусный») трафик на тест. Русскоязычная аудитория. Без рекламы!
Пользователям
Вам захотелось отдохнуть? Или просто приятно провести время? Выбирайте и проходите онлайн-тесты, делитесь результатом с друзьями. Проверьте, смогут они пройти также как Вы, или может лучше?
Внимание! Наши тесты не претендуют на достоверность – не стоит относиться к ним слишком серьезно!
Классификация признаков



Почему важно знать классификацию признаков (иногда говорят шкалы измерения)? Тип признака во многом определяет те статистические методы, которые могут быть применены для обработки данных. В литературе встречаются различные классификации, но все они достаточно близки друг к другу и предлагаемая ниже вполне достаточна для освоения основ биостатистики.
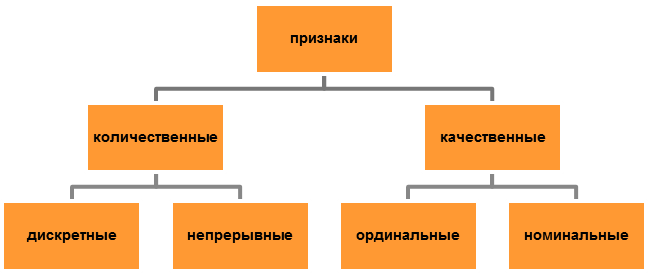
Различают количественные и качественные признаки. Количественные признаки выражаются числами. Значения количественных признаков могут быть непрерывными или дискретными. Дискретные – это признаки, значения которых отличаются не менее чем на единицу измерения признака (число человек в семье, койко-дни). Непрерывные признаки – это признаки, значения которых могут отличаться друг от друга на любую сколь угодно малую величину (рост, вес человека, объем).
Рисунок 5. Классификация признаков
Качественные признаки выражаются категориями. В свою очередь они в зависимости от вида данных делятся на номинальные (классификационные) и ординальные (порядковые). Говорят также, что соответствующие качественные признаки измеряются в номинальной или порядковой шкале. Разница между этими шкалами состоит в следующем.
Признак, измеряемый в номинальной шкале, принимает одно значение из конечного числа заведомо установленных градаций. Примерами признаков, измеряемых в номинальной шкале, являются пол (мужской, женский), цвет глаз (карие, зеленые, серые), классификация животных и т. п. Статистические данные, измеряемые в номинальных шкалах, представляются в виде таблиц, в которых приводятся частоты появления той или иной градации признака. Часто номинальные данные появляются при обработке эпидемиологических данных. Например, может представлять интерес вопрос о частоте встречаемости того или иного признака при том или ином заболевании.
Значения качественных признаков, измеряемых в ординалъной шкале, могут быть упорядочены, т.е. расположены по возрастанию или убыванию. Примерами таких признаков являются качество условий жизни (плохое, удовлетворительное, хорошее, очень хорошее), температура (нормальная, повышенная, высокая, очень высокая), шкала оценки боли. Для признаков, измеряемых в ординальных шкалах, операции сложения и вычитания не имеют смысла. Так, нельзя сказать, что студент, получивший на экзамене «пять» по статистике знает предмет на одну единицу лучше, чем студент, получивший по этому предмету «четыре», поскольку для знаний не существует единицы измерения. Однако можно сказать, что первый студент знает статистику лучше, чем второй.
Для представления значений ординальных признаков в числовой форме используется следующий способ. Все значения признака записываются в порядке возрастания в виде ряда. Каждому значению ставится в соответствие натуральное число, равное его номеру в ряду. Это число называется рангом. Например, качество условий жизни (плохое, удовлетворительное, хорошее, очень хорошее) будет представлено рангами 1, 2, 3, 4. Для ординальных признаков, представленных в виде рангов, разработаны специальные статистические методы, позволяющие измерять степень близости признаков (например, ранговая корреляция), проверять гипотезы о виде распределения, проводить дисперсионный анализ.
Для данных, представленных в номинальной шкале, также не определены операции сложения и вычитания. Эти данные (в отличие от ординальных признаков) не могут быть упорядочены и, следовательно, оцифрованы с помощью рангов. Применяя специальные статистические методы для номинальных признаков, можно проверить гипотезы о независимости признаков и о принаддежности двух или нескольких выборок к одной совокупности.
Контрольное задание 1 (тесты)
1. Как называются признаки, значения которых отличаются не менее чем на единицу измерения
a) дискретные признаки
b) непрерывные признаки
c) ординальные признаки
d) номинальные признаки
e) качественные признаки
2. Какие признаки называются ординальными
a) признаки, значения которых отличаются не менее чем на единицу измерения признака
b) признаки, значения которых могут отличаться на любую сколь угодно малую величину
c) качественные признаки, которые можно упорядочить
d) признак принимает одно значение из конечного числа заведомо установленных градаций, которые невозможно упорядочить
e) качественные признаки
3. Какие из данных являются ординальными признаками
a) национальность рабочих
c) цвет глаз, цвет волос
d) пол, классификация животных
e) количество детей, средняя заработная плата
4. В целях обследования состояния здоровья населения от 18 до 25 лет было охвачено 1000 студентов различных ВУЗов. Какой является совокупность по полноте охвата
Классификация признаков
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
АГ – артериальная гипертония
АД – артериальное давление
ДК – диагностический коэффициент
ДЭ – диагностическая эффективность теста
ИМТ – индекс массы тела
ИО – истинно отрицательный результат
ИП – истинно положительный результат
ЛО – ложноотрицательный результат
ЛП – ложноположительный результат
ЛПВП – липопротеиды высокой плотности
МНК – метод наименьших квадратов
ОР – относительный риск
ОШ – отношение шансов
ППП STATISTICA – пакет прикладных программ STATISTICA
ЧСС – частота середечных сокращений
ПРЕДИСЛОВИЕ
Сегодня уже не стоит вопрос «нужна ли статистика врачу?». В эпоху развития доказательной медицины потребность в применении статистики в медицине и биологии стало необходимостью. В программы до- и послевузовского медицинского образования всех специальностей включена биологическая статистика. Очевидно, что врач не станет специалистом в области статистического анализа, однако, он должен знать основные задачи, которые стоят перед этой областью знаний, и, самое главное, понимать, что статистика помогает дать клиническую оценку результатам исследования эффективности профилактических, диагностических и лечебных мероприятий и процедур. Во–первых, врачу нужно иметь набор статистических знаний, позволяющих ему критически оценивать качество научных публикаций на медицинскую тематику. При этом не требуется достаточно глубоких теоретических знаний по статистике, вполне можно обойтись основами статистического анализа, знать ограничения по их использованию и разумные требования по описанию этих методов в публикациях. Во-вторых, врач может и сам участвовать в научных исследованиях, использовать статистику как средство анализа групповых свойств, при этом он должен владеть определенными навыками подбора методов, оценивать их достоинства и недостатки, уметь работать со статистическими программами, делать правильные выводы из полученных результатов.
Предлагаемое вашему вниманию издание является дополнением к уже выпущенному ранее учебному пособию «Биостатистика: в примерах и задачах». Если первая книга была посвящена в основном методам решения статистических задач, то теперь появилась необходимость изложить простым, «нематематизированным» языком основные цели и задачи биостатистики, теоретические основы статистических методов, показать, как эти методы позволяют решать конкретные медицинские проблемы. Также в книгу включены разделы, которые выходят за рамки додипломного образования, и будут полезны обучающимся в магистратуре и докторантуре при выполнении их научных работ. Надеемся, что книга будет полезна всем, кто хочет приобщиться к миру статистических знаний.
ЗАДАЧИ БИОСТАТИСТИКИ
Ниже приведены наиболее распространенные определения статистики вообще, и биостатистики в частности.
Статистика – отрасль знаний (наука), изучающая методы сбора, систематизации, обработки и интерпретации результатов наблюдений с целью выявления статистических закономерностей.
Биостатистика (биометрика) – отрасль знаний, связанная с разработкой и использованием статистических методов в научных исследованиях в медицине, здравоохранении и эпидемиологии.
Чтобы вникнуть в суть этих определений выясним, в чем была необходимость появления биостатистики, какие задачи она решает?
В своей практической деятельности врач, как правило, имеет дело с одним пациентом (в дальнейшем будем использовать термин биообъект), измеряет какие-то показатели его здоровья (признаки), ставит диагноз и назначает лечение. Это единичное явление, отдельный акт. Например, измерив рост одного человека, мы сразу делаем вывод: высокий, среднего роста он или низкорослый. А как поступить, если нам надо описать группу людей, учитывая, что они все разного роста (рисунок 1).
Рисунок 1. Пример группового свойства
| Хср=178 см |
| Хср=178 см |
Первое, что приходит на ум – это определить средний рост. Теперь задумайтесь, а что это нам дает, какую информацию о росте людей в данной группе несет среднее значение. Многих такой вопрос ставит в тупик. Давайте обратимся к рисунку 2.
Рисунок 2. Сравнение групповых свойств
Из него видно, что при равенстве средних значений рост людей в двух группах значительно разница. Отсюда можно сделать вывод, что для их сравнения одних только средних недостаточно. По-видимому, нужны еще какие-то показатели.
Еще один пример приведен на рисунке 3. Это результаты измерения артериального давления до и после приема некоторого гипотензивного препарата. В исследовании приняли участие две группы.


Рисунок 3. Изменение артериального давления после приема препарата
Теперь перейдем ко второй задаче биостатистики. Предположим, что в предыдущем примере с гипотензивным препаратом, испытанном на 7 больных, вы сделали вывод о его эффективности. Можем ли мы на этом основании предложить его для массового выпуска, будет ли он помогать и другим, тысячам, страдающим повышенным артериальным давлением? Наверное, многие ответят нет, не можем. Что же в таком случае делать, как проверить это средство, ведь как бы мы не увеличивали количество привлеченных к испытаниям лиц, все равно не сможем охватить всю совокупность гипертоников земного шара (в статистике используют термин генеральная совокупность). А ведь только это нас и интересует, а не результаты какого-то отдельного (выборочного) исследования, ведь мы предполагаем назначать препарат повсеместно. Статистические методы позволяют перенести результаты выборочных исследований на всю генеральную совокупность объектов, но с учетом, что есть вероятность ошибочности нашего утверждения. И если эта вероятность невелика, то мы принимаем сделанные выводы, в противном случае – отвергаем. Вопрос о том велика или невелика ошибка решает сам исследователь, исходя из сути решаемой проблемы. Например, я утверждаю, что данный препарат эффективен во всей генеральной совокупности, при этом вероятность ошибки составляет 0,05 (т.е. 5 %) и это меня вполне устраивает. Возможно, у кого-то другого более жесткие требования и он удовлетвориться только вероятностью ошибки не более 0,01 (1%).
Следующий случай продемонстрирует нам, к каким последствиям может привести незнание законов статистики и неумение ими пользоваться. Случай этот выдуманный, но весьма показательный. Фармкомпания разработала лекарственное средство, позволяющее повысить уровень гемоглобина, и испытало его на выборке из 5 человек. Результаты, приведенные на графике 4А, позволяют говорить о высокой его эффективности, ведь чем выше доза препарата, тем выше уровень Hb.

Рисунок 4. Результаты испытания препарата на выборках различного объема
На основании этих данных было налажено массовое производство, вложены значительные финансовые и людские ресурсы. Однако, время показало, что препарат залежался на складах и его не назначают врачи. Озадачившись, ученые провели повторное, более массовое испытание и вот, что оно дало – одна и та же доза может быть эффективной для одних лиц и неэффективной для других (рисунок 4Б). Отнеся результаты выборочных исследований на всю генеральную совокупность, исследователи не оценили вероятность ошибки полученных результатов, а она была, по-видимому, значительной, т.е. полученная эффективность носила случайный характер.
Таким образом, мы фактически сформулировали вторую задачу биостатистики. Смысл ее в принятии наиболее обоснованного суждения относительно свойств и характеристик генеральной совокупности с опорой на результаты изучения выборки.Эта задача рассматривается в разделе, называемом теорией проверки статистических гипотез.
Статистические методы позволяют также решать задачи выявления взаимозависимостей между признаками, изучения динамики состояния биообъектов во времени, задачи классификации и прогнозирования.
Основные понятия и определения биостатистики
Терминология имеет важное значение в любой области знаний, поскольку, не владея ею, нельзя понять суть излагаемого, и соответственно невозможно использовать знания на практике. Проблема состоит еще в том, что различные авторы или коллективы, научные школы могут использовать различную терминологию. Так, с советских времен в статистике закрепились термины и обозначения, отличающиеся от тех, что приняты в зарубежной литературе. Поэтому нам необходимо определиться с терминологией, которую будем использовать в дальнейшем.
Любой биообъект характеризуется какими-либо признаками. Например: рост, вес, артериальное давление, пульс, уровень гемоглобина, цвет глаз и т.д. При измерении этих признаков у разных объектов получаем статистические данные. Если у каждого объекта измеряется один признак (например, гемоглобин), то получаются одномерные данные, если два признака (гемоглобин и ЧСС) – то данные двумерные, и т.д. – многомерные.
Пусть измерен пульс у разных людей и получены статистические данные: 65, 68, 72, 75, 80, 60, 65, 64, 61, 77, 73, 73, 69, 60…..
С математической точки зрения пульс представляет собой случайную величину. Это одно из основных понятий теории вероятности, на которую во многом опирается статистика. Случайной величинойX (x1, x2, x3 …..xi……xn) называется величина, которая в результате опыта может в определенных пределах принять то или иное значение, неизвестно заранее какое именно.
Как правило (но не всегда), генеральная совокупность имеет очень много элементов (объектов), либо они труднодоступны. Поэтому обследуется некоторая часть генеральной совокупности – выборочная совокупность (выборка). Количество объектов в выборочной совокупности называется объемом выборки (n).
Выборка должна давать правильное, неискаженное представление о генеральной совокупности, или, как говорят, быть репрезентативной. Например, нельзя судить о заболеваемости кишечными инфекциями, обследуя только районы с высокими социально-экономическими условиями.
Как мы уже отмечали, результаты исследования выборки с определенной долей вероятности распространяются на всю генеральную совокупность, т.е. определяется их статистическая значимость.
Классификация признаков
Почему важно знать классификацию признаков (иногда говорят шкалы измерения)? Тип признака во многом определяет те статистические методы, которые могут быть применены для обработки данных. В литературе встречаются различные классификации, но все они достаточно близки друг к другу и предлагаемая ниже вполне достаточна для освоения основ биостатистики.
Различают количественные и качественные признаки. Количественные признаки выражаются числами. Значения количественных признаков могут быть непрерывными или дискретными. Дискретные – это признаки, значения которых отличаются не менее чем на единицу измерения признака (число человек в семье, койко-дни). Непрерывные признаки – это признаки, значения которых могут отличаться друг от друга на любую сколь угодно малую величину (рост, вес человека, объем).
Рисунок 5. Классификация признаков
Качественные признаки выражаются категориями. В свою очередь они в зависимости от вида данных делятся на номинальные (классификационные) и ординальные (порядковые). Говорят также, что соответствующие качественные признаки измеряются в номинальной или порядковой шкале. Разница между этими шкалами состоит в следующем.
Признак, измеряемый в номинальной шкале, принимает одно значение из конечного числа заведомо установленных градаций. Примерами признаков, измеряемых в номинальной шкале, являются пол (мужской, женский), цвет глаз (карие, зеленые, серые), классификация животных и т. п. Статистические данные, измеряемые в номинальных шкалах, представляются в виде таблиц, в которых приводятся частоты появления той или иной градации признака. Часто номинальные данные появляются при обработке эпидемиологических данных. Например, может представлять интерес вопрос о частоте встречаемости того или иного признака при том или ином заболевании.
Значения качественных признаков, измеряемых в ординалъной шкале, могут быть упорядочены, т.е. расположены по возрастанию или убыванию. Примерами таких признаков являются качество условий жизни (плохое, удовлетворительное, хорошее, очень хорошее), температура (нормальная, повышенная, высокая, очень высокая), шкала оценки боли. Для признаков, измеряемых в ординальных шкалах, операции сложения и вычитания не имеют смысла. Так, нельзя сказать, что студент, получивший на экзамене «пять» по статистике знает предмет на одну единицу лучше, чем студент, получивший по этому предмету «четыре», поскольку для знаний не существует единицы измерения. Однако можно сказать, что первый студент знает статистику лучше, чем второй.
Для представления значений ординальных признаков в числовой форме используется следующий способ. Все значения признака записываются в порядке возрастания в виде ряда. Каждому значению ставится в соответствие натуральное число, равное его номеру в ряду. Это число называется рангом. Например, качество условий жизни (плохое, удовлетворительное, хорошее, очень хорошее) будет представлено рангами 1, 2, 3, 4. Для ординальных признаков, представленных в виде рангов, разработаны специальные статистические методы, позволяющие измерять степень близости признаков (например, ранговая корреляция), проверять гипотезы о виде распределения, проводить дисперсионный анализ.
Для данных, представленных в номинальной шкале, также не определены операции сложения и вычитания. Эти данные (в отличие от ординальных признаков) не могут быть упорядочены и, следовательно, оцифрованы с помощью рангов. Применяя специальные статистические методы для номинальных признаков, можно проверить гипотезы о независимости признаков и о принаддежности двух или нескольких выборок к одной совокупности.
Математическая статистика
Анализ статистических взаимосвязей
Виды связей между величинами
При изучении объектов и явлений исследователю, как правило, приходится иметь дело с несколькими некоторым образом связанными статистическими признаками. Например, объём продукции предприятия связан с численностью работников, мощностью оборудования, стоимостью производственных фондов и еще многими признаками. Признаки «пол» и «число лейкоцитов в крови» могли бы рассматриваться как зависимые, если бы большинство мужчин имело высокий уровень лейкоцитов, а большинство женщин – низкий, или наоборот. Рост связан с весом, потому что обычно высокие индивиды тяжелее низких; IQ (коэффициент интеллекта) связан с количеством ошибок в тесте, т.к. люди высоким значением IQ делают меньше ошибок и т.д.
Невозможно управлять явлениями, предсказывать их развитие без изучения характера, силы и других особенностей связей. Поэтому методы исследования, направленные на измерение связей, составляют чрезвычайно важную часть методологии научного исследования, в том числе и статистического.
При исследовании причинно-следственных связей статистические признаки разделяют на факторные и результативные. Факторные признаки, или факторы, – это признаки, обуславливающие изменение других, связанных с ними, признаков. Результативными называются признаки, изменяющиеся под воздействием факторных признаков.
Различают два типа связей между факторными и результативными признаками: функциональную и статистическую. Функциональной называют такую связь, при которой каждому определённому значению x факторного признака соответствует одно и только одно значение y результативного признака:
Функциональная зависимость результативного признака y от многих факторов x1,…,xk возможна только в том случае, если признак y всегда зависит от перечисленного набора факторов и ни от чего более. Такие связи также являются абстракциями, поскольку большинство явлений и процессов безграничного реального мира связаны между собой, и нет такого конечного числа переменных, которые абсолютно полно определяли бы собою зависимую величину. Тем не менее, на практике нередко используют представление реальных связей как функциональных. Например, длина года (период обращения Земли вокруг Солнца) почти функционально зависит только от массы Солнца и расстояния Земли от него. На самом деле она зависит в очень слабой степени и от масс, и от расстояний других планет от Земли, но вносимые ими (и тем более в миллионы раз более далекими звездами) искажения функциональной связи для всех практических целей, кроме космонавтики, пренебрежимо малы.
Такие связи имеют место, например, если на результативный признак действуют несколько факторных признаков, а для описания связи используется один или несколько определяющих (учтённых) факторов.
Частным случаем статистической связи между результативным и факторным признаками y и x является корреляционная связь. При корреляционной связи от значения x факторного признака зависит не всё распределение вероятностей FY(y), а лишь математическое ожидание величины Y. Математическое ожидание случайной величины Y при фиксированном значении случайной величины X = x называется условным математическим ожиданием и обозначается M[Y|x], а уравнение
В зависимости от типа рассматриваемых статистических признаков для анализа статистических связей между ними используют различные статистические методы (табл. 6.1).
Для анализа степени тесноты связи между количественными факторным и результативным признаками, т.е. признаками, варианты которых имеют числовое выражение, используются методы корреляционного анализа, для анализа уравнения регрессии – методы регрессионного анализа. Корреляционный и регрессионный анализы также могут быть применены для случая качественных порядковых, или ординальных, признаков, т.е. признаков, значения которых могут быть некоторым образом упорядочены. Для таких признаков можно сказать, какие значения больше или меньше, но нельзя сказать насколько.
В случае если факторный признак является номинальным (категориальным, или атрибутивным), т.е. признаком, варианты которого могут быть измерены только в терминах принадлежности к некоторым категориям, а результативный – количественным, то для анализа статистической связи между ними используются методы дисперсионного анализа.
Если же оба признака – и факторный, и результативный – являются номинальными, то для анализа статистической связи между ними используют метод таблиц сопряжённости.
Если факторный признак является количественным, а результативный – номинальным, то задачу, как правило, сводят к случаю двух номинальных признаков путём группировки значений факторного признака.