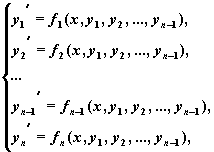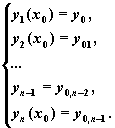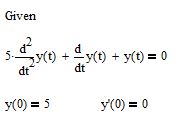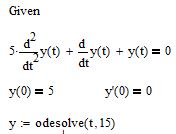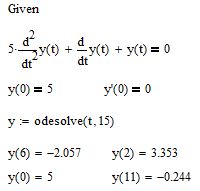что такое odesolve в маткаде

Что такое odesolve в маткаде

Для решения дифференциальных уравнений Mathcad предоставляет пользователю библиотеку встроенных функций Differential Equation Solving, предназначенных для численного решения дифференциальных уравнений.

ODESOLVE

Полную информацию о правилах использования функции odesolve можно получить во встроенном справочнике Mathcad в разделе Overview fnd Tutorials.

Функции для решения систем, записанных в нормальной форме

Встроенные функции Mathcad, предназначенные для решения задачи Коши и граничных задач, решают их для нормальных с и с т е м обыкновенных дифференциальных уравнений. Задачи для уравнений высших порядков сводятся к соответствующим задачам для нормальных с и с т е м.

Рассмотрим задачу Коши:

, ,

,

,

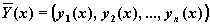
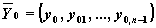
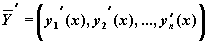
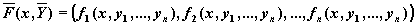
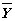
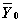
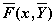
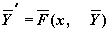
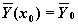
где — искомое решение, — вектор начальных условий, а — вектор правых частей, запишем систему дифференциальных уравнений в векторной форме:

, .

Смысл параметров для всех функций одинаков и определяется математической постановкой задачи:
y — вектор начальных условий , ;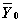
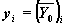
x1, x2 — начальная и конечная точки отрезка интегрирования системы; для функций, вычисляющих решение в заданной точке, x1 — начальная точка, x2 — заданная точка;
npoints — число узлов на отрезке [x1, x]; при решении задачи на отрезке результат содержит npoints+1 строку;
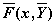
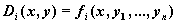
D — имя вектор-функции D(x,y) правых частей , ; ( имя D – от Derivative — производная, имя вектора, содержащего выражения для производных (derivatives) искомого решения);
J — имя матрицы-функции J(x,y) размерности n x (n+1), в первом столбце которой хранятся выражения частных производных по x правых частей системы, а в остальных n столбцах содержится матрица Якоби правых частей: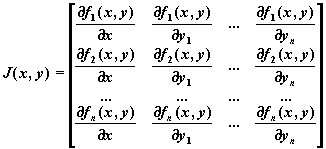
.
acc — параметр, контролирующий погрешность решения при автоматическом выборе шага интегрирования (если погрешность решения больше acc, то шаг сетки уменьшается; шаг уменьшается до тех пор, пока его значение не станет меньше save );
kmax — максимальное число узлов сетки, в которых может быть вычислено решение задачи на отрезке, максимальное число строк в результате;
save — наименьшее допустимое значение шага неравномерной сетки.

При исследовании автономных систем дифференциальных уравнений второго порядка полезную информацию можно получить рассматривая интегральные и фазовые кривые системы.

При исследовании автономных систем дифференциальных уравнений второго порядка полезную информацию о свойствах решений можно получить, построив векторное поле системы.

Запишем автономную систему второго порядка

.

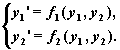
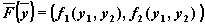
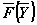
Эта система полностью определяется заданием векторного поля , поскольку векторное поле задает в каждой точке направление касательной к фазовой кривой системы, проходящей через эту точку.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

MathCAD — это просто! Часть 22. Другие методы численного решения дифференциальных уравнений

В прошлый раз мы с вами обсуждали вопросы решения дифференциальных уравнений в мощнейшей из математических сред (то есть в MathCAD) с помощью встроенной функции Odesolve. Функция эта, как мы с вами успели выяснить, в общем-то, всем хороша, однако, как я уже успел в прошлый раз обмолвиться, она предлагает не единственный из всех возможных путей численного решения дифференциальных уравнений в MathCAD. Для того, чтобы чувствовать себя в MathCAD’е как рыба в воде, нужно в совершенстве овладеть всеми способами решения дифференциальных уравнений. Ну, а для начала, наверное, стоит познакомиться с этими самыми способами с помощью вот этой статьи. Кроме того, мы с вами разберемся с такими вопросами, как решение систем «диффуров», поскольку системы дифференциальных уравнений встречаются едва ли не чаще, чем уравнения одиночные. В общем, планы, как видите, прямо-таки наполеоновские, а потому не буду затягивать вступления, а перейду к самому рассказу о работе с дифференциальными уравнениями в MathCAD’е.

Выбор метода интегрирования

Если вы еще помните наш с вами разговор о численном интегрировании в среде MathCAD, то должны помнить и о том, что можно выбирать разные методы интегрирования в зависимости от задачи. В общем-то, поскольку решение дифференциальных уравнений — это, по большому счету, то же самое интегрирование, разумно было бы ожидать, что и при решении ДУ можно будет выбирать метод интегрирования. И действительно, MathCAD (как, впрочем, и всегда) не обманывает наших ожиданий: выбирать способ вычисления решения дифференциального уравнения при использовании функции Odesolve и можно, и нужно.

Хитрости в изменении метода интегрирования для Odesolve никакой нет. Достаточно кликнуть правой кнопкой мыши по названию функции и выбрать в появившемся меню один из трех вариантов: Fixed, Adaptive или Stiff. Думаю, имеет смысл все же сделать некоторые пояснения по поводу того, чем различаются данные способы интегрирования дифференциальных уравнений. Fixed использует фиксированный шаг интегрирования, а Adaptive, как можно понять уже из его названия, — адаптивный (то есть изменяющийся). Если вы не очень хорошо представляете себе, что это все означает, и как они друг от друга отличаются, то имеет смысл вернуться к той статье про численное интегрирование в MathCAD’е, в которой я довольно подробно об этом всем рассказывал. Что касается метода Stiff, то он довольно специфичен и используется для так называемых жестких систем. Если вы работаете с ними, то вы сами знаете, что они жесткие, и вам следует устанавливать флажок именно напротив этого пункта меню. Если же, скажем так, в жесткости системы возникают сомнения, то лучше всего использовать метод Adaptive, потому что он гарантирует более высокую точность решения и избавляет пользователя от хлопот, связанных с подбором правильного шага интегрирования.

Использование функции rkfixed

Как я уже говорил во вступлении к статье, функция Odesolve является не единственным возможным вариантом применяемой для решения дифференциальных уравнений функции. Сейчас мы с вами рассмотрим функцию rkfixed, которая также может быть успешно использована для их решения. Вы можете спросить, зачем нужна еще одна функция для численного решения дифференциальных уравнений, если Odesolve и так самым что ни на есть замечательным образом справляется со своими прямыми обязанностями. Что ж, вопрос резонный, но на самом деле хронологически Odesolve появилась в MathCAD’е позже, чем некоторые другие функции для решения дифференциальных уравнений (в том числе rkfixed). В общем-то, пожалуй, можно было бы и не говорить о более старых функциях, поскольку Odesolve более проста для пользователя в силу своей универсальности, однако бывают случаи, когда приходится сталкиваться и со старыми функциями, которые в новых версиях MathCAD оставлены, в основном, из соображений обратной совместимости со старыми версиями этой математической среды. Поэтому, если вам придется столкнуться с документами, сделанными в старых версиях MathCAD’а, в которых используется для решения дифференциальных уравнений функция rkfixed, то вы не будете пребывать в растерянности, а сможете разобраться, что именно хотел вычислить автор данного документа.

Итак, rkfixed. Пользоваться этой функцией, по сути дела, нужно точно так же, как и Odesolve. То есть сначала должны идти начальные условия для уравнения, а также само уравнение, оформленное в виде функции двух переменных (т.е. dy/dx = f(x, y)). К сожалению, функция rkfixed позволяет решать уравнения исключительно такого вида, а потому, например, работать с уравнением второго порядка вам придется с ее помощью уже как с системой двух дифференциальных уравнений. Помимо этого, нужно указать количество шагов интегрирования, для которых будут рассчитываться значения решения нашего дифференциального уравнения. Использования функции rkfixed вы можете на соответствующей иллюстрации к статье. Из нее, кстати, несложно понять, какие аргументы мы передаем в функцию для решения ДУ. Первый параметр — это начальное значение аргумента, по которому берется производная; второй и третий — это, соответственно, начало и конец того отрезка, на котором будет производиться интегрирование; четвертый параметр — это количество шагов интегрирования, ну, а последний — собственно сама функция f(x, y) для нашего уравнения dy/dx = f(x, y).

Как видите, использовать Odesolve действительно проще и удобнее. Помимо rkfixed, в MathCAD’е есть и другие функции, которые позволяют решать ДУ не с использованием фиксированного шага, а с адаптивным методом интегрирования или со специальными методами решения некоторых видов уравнений. Найти их в справке MathCAD’а не представит никакой сложности, кроме того, мы еще поговорим немного ниже о них. Однако их, как и rkfixed, рекомендуется по возможности не применять, заменяя на Odesolve.

Решение систем дифференциальных уравнений

Что ж, с одиночными дифференциальными уравнениями мы с вами, в общем-то, можно считать, практически разобрались. Конечно, было бы интересно узнать, как работают алгоритмы, лежащие в основе методов численного решения ДУ в MathCAD’е. Возможно, в следующий раз нам с вами и удастся об этом поговорить. Пока же на очереди вопрос более насущный и важный — решение систем дифференциальных уравнений. Поспешу вас обрадовать: мы с вами уже почти умеем решать системы дифференциальных уравнений — недаром же мы с вами останавливались на вопросах использования такой, казалось бы, устаревшей и не сильно для нас с вами полезной функции, как rkfixed. Оказывается, именно она поможет нам решать системы дифференциальных уравнений, с которыми, к сожалению, функция Odesolve никаких дел иметь не хочет. Использование функции rkfixed (и некоторых других) для решения систем ДУ имеет самые что ни на есть минимальные отличия от ее же использования в случае одиночных уравнений. По сути дела, для самого MathCAD’а отличий и вовсе никаких нет — просто скалярные переменные в этой функции заменяются на векторные, с которыми она работает точно так же, как и со скалярными. При этом, правда, действует все то же ограничение на вид уравнений, входящих в систему: они должны быть линейными и не содержать производных выше первой. Впрочем, как я уже говорил, ограничение, связанное с производными высших порядков, довольно просто обходится.

Вы легко обнаружите на иллюстрации к статье, демонстрирующей решение системы уравнений с помощью rkfixed, что совсем не так уж много отличий между решением системы и решением одиночного дифференциального уравнения. Кстати, если внимательно присмотреться к решенной на иллюстрации системе, то можно обнаружить, что она как раз и относится к тому «хитрому» способу решения дифференциальных уравнений второго порядка, к которому приходится прибегать при использовании для решения функции rkfixed.

Теперь, пожалуй, стоит рассказать немного о других функциях, аналогичных по сути rkfixed, но работающих несколько иначе. Функция rkfixed (как видно из ее названия) использует для интегрирования фиксированный шаг, что, с одной стороны, обеспечивает приемлемую точность интегрирования, а с другой — его высокую скорость. Но иногда этой точности бывает недостаточно, и тогда имеет смысл применить функцию rkadapt. В отличие от rkfixed, она имеет изменяющийся соответственно скорости изменения интегрируемой функции шаг интегрирования, а потому в случае быстро изменяющихся функций имеет смысл применять именно ее. Впрочем, ее лучше привыкнуть применять всегда, поскольку адаптивный шаг интегрирования позволяет добиться большей точности результатов вычисления решения дифференциального уравнения. Еще одна функция, которая может применяться в процессе решения — Bulstoer. Она позволяет достигать еще большей точности интегрирования, однако применять ее можно только тогда, когда интегрируемая функция будет достаточно гладкой и достаточно медленно изменяющейся. Насколько именно гладкой и медленно изменяющейся должна быть функция, можно попробовать установить экспериментально, сравнив результаты решения с применением каждой из этих трех функций. Как вы понимаете, все они имеют одинаковые параметры, и, поскольку мы уже разобрали параметры rkfixed, то для двух остальных функций мы их разбирать не будем.

Что ж, сказано всего в этот раз о численном решении дифференциальных уравнений и их систем было, как всегда, немало, и настало время по традиции подвести итоги. Как видите, решать системы дифференциальных уравнений в MathCAD уже не так просто, как одиночные уравнения, но, в принципе, это все было вполне ожидаемо, и ничего такого особенно трагичного в этом, как мне кажется, нет. Если не бояться их решать, то решать совсем не так уж и сложно — в любом случае, куда как проще, чем с помощью ручки и бумаги. Впрочем, как видите, решение дифференциальных уравнений и их систем сопряжено с рядом довольно-таки тонких моментов, например, касательно того, какой метод интегрирования выбрать. Для того, чтобы не допустить досадной ошибки, отрицательно влияющей на результат, мало просто быть знакомым с разными методами интегрирования — надо еще хорошо представлять себе особенности решаемой с помощью MathCAD задачи и применяемых в ней функций. То есть, несмотря на всю свою мощь, MathCAD все-таки не может освободить вас от знаний высшей математики, потому что это не компьютерный решатель задач, а всего лишь мощный «навороченный» калькулятор. И успехов при работе с MathCAD можно достичь только если подходить к нему именно как к помощнику, а не как к универсальному математическому решателю.

Компьютерная газета. Статья была опубликована в номере 36 за 2008 год в рубрике soft

Источник

Что такое odesolve в маткаде

Глава 5. Решение дифференциальных уравнений

Применение функции Odesolve требует записи вычислительного блока, состоящего из трех частей:

1) ключевого слова Given (Дано);

2) дифференциального уравнения и начальных или граничных условий к нему;

Примеры использования функции Odesolve приведены на рис. 5.2–5.5.

Given

граничные условия можно задавать лишь в двух точках:

в начале и в конце интервала интегрирования

Рис. 5.2 Решение уравнения с граничными условиями

MathCAD позволяет записать условие несколькими способами:

– с использованием булевых операторов:

;

– с использованием функции if :

.

поменяйте местами закрашенные выражения

Given

Рис. 5.3 Объединение двух дифференциальных уравнений в одно

В MathCAD 2001 i возможности функции Odesolve были расширены. Теперь она может решать и системы дифференциальных уравнений. При этом несколько изменяется обращение к ней.

Дано уравнение

решим его относительно у'(х)

has solution(s)

два корня уравнения дают решение ОДУ

Given

Рис. 5.4 Приведение дифференциального уравнения к стандртному виду и его решение

Обращение к функции для решения одного уравнения выглядит так:

для решения системы дифференциальных уравнений–

Если график строится для значений, выходящих за пределы интервала интегрирования, MathCAD экстраполирует значения функции за пределы интервала интегрирования, получая чаще всего неправдоподобные результаты.

Если в MathCAD 11 функция Odesolve решает системы уравнений только с начальными параметрами, то в MathCAD 12, 13, 14 – и с начальными, и с граничными условиями.

поменяйте вид уравнений и граничные условия

Рис. 5.5 Решение системы ОДУ функцией Odesolve

В MathCAD 2001 i у функции Odesolve появилась возможность принимать в качестве ограничений алгебраические уравнения (рис. 5.6 и 5.7), но только в задачах с начальными условиями.

дифференциальные

уравнения

алгебраическое уравнение

требуется 6 начальных условий:

Рис. 5. 6 Решение системы ОДУ с алгебраическими ограничениями функцией Odesolve

Given

Рис. 5.7 В ыбор метода решения дифференциальных уравнений

Источник

Решение дифференциальных уравнений в MathCad 15

В статье рассмотрена работа функции odesolve для графического решения дифференциального уравнения в программе mathcad версии 15 и старше

Функция odesolve

Для примера рассмотрим простейшее дифференциальное уравнение, описывающее затухающие колебания маятника с течением времени

В свободном поле mathcad введите оператор Given. Этот оператор запускает процесс ввода исходных данных для корректной работы функции odesolve. После этого найдите панель под названием Calculus. В этой панели нам понадобятся кнопки Derivative и Nth Derivative. Эти кнопки вводят заготовки для дифференциального уравнения. С помощью клавиатуры введите уравнение, как показано на рисунке 1. Знак равенства необходимо использовать из панели Boolean

Рис. 1. Ввод исходных данных для решения дифференциального уравнения

Далее введите начальные приближения. Количество начальных приближений зависит от порядка дифференциального уравнения. В нашем случае их будет 2. Введите приближения, как показано на рисунке 2. Обратите внимание, что для ввода значания первой производной вам нужно использовать символ «верхний апостроф«. Если вы его не можете ввести с клавиатуры вручную воспользуйтесь приложением windows Capter Map или используйте комбинацию клавиш Alt + 96 или Alt + 39

Рис. 2. Ввод первого приближения для решения дифференциального уравнения

Теперь, после начального приближения введите любую переменную (например y) и присвойте ей функцию Odesolve, как показано на рисунке 3. В качестве параметров функции Odesolve используется переменная t и интервал интегрирования. В нашем случае интервал равен 15

Рис. 3. Ввод функции odesolve для решения дифференциального уравнения

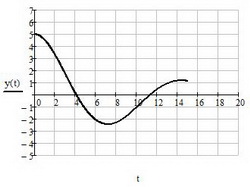
Можно отобразить функцию y на графике, где в качестве аргумента будет переменная t. Этот график и будет являться решением дифференциального уравнения. Обратите внимание, что график строится в пределах интервала интегрирования. Особенности оформления и отображения графиков в mathcad 15 смотрите в соответствующем разделе

Рис. 4. Вывод результата решения дифференциального уравнения на график

После корректного решения дифференциального уравнения функцию y(t) можно использовать далее в расчетах

Рис. 5. Результат решения дифференциального уравнения в mathcad 15 и старше

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Источник