Что такое функция возрастающая убывающая функция
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Возрастание и убывание функции
Что такое возрастающие и убывающие функции
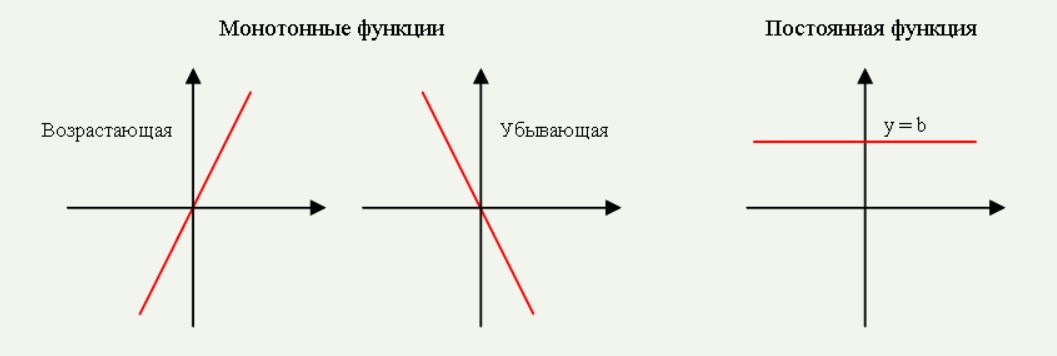
Монотонная функция — функция, изменяющаяся исключительно в одном и том же направлении.
И убывающая, и возрастающая функции относятся именно к понятию монотонной.
Возрастающая функция — линейная функция, возрастающая при увеличении значения аргумента.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Убывающая функция — линейная функция, убывающая при увеличении значения аргумента.
Также важно знать, что существует постоянная функция, значение которой не меняется на всем промежутке графика.
Свойства и признаки, пример
Достаточными условиями для возрастания или убывания функций являются следующие признаки:
Кроме этого, у монотонных функций есть характерные особенности, называемые свойствами. Они помогают в решении задач различной сложности: начиная от функций с логарифмами и заканчивая неравенствами с функциями. Свойства:
Рассмотрим пример-доказательство для убывающей функции:
Возьмем точки x1 и x2, чтобы \(0\leq x_1\leq x_2.\) Посмотрим на разность значений функции в данных точках.
Возрастающими являются также следующие функции:
Возрастание и убывание функции
Общие понятия о поведении функций
Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.
Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.
Соответственно, монотонная функция может быть возрастающая или убывающая.
Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.
Математическое выражение этого определения выглядит следующим образом:
Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.
Математическое выражение этого определения выглядит следующим образом:
Разберем примеры решения задач на изучение характера поведения функции.
Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.
Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.
Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.
Не нашли что искали?
Просто напиши и мы поможем
Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.
Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.
То есть функция \(y=5\) будет постоянной.
Постоянная, не убывающая и не возрастающая функции не есть монотонные.
Свойства монотонных функций
К свойствам монотонных функций относятся такие характеристики:
Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:
Возрастание и убывание функции на интервале, экстремумы
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Точки экстремума, экстремумы функции
Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.
Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Иначе говоря, получим их условия постановки знака:
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
После чего необходимо найти производную:
Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
Изображение на прямой имеет вид
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
Перейдем к вычислению минимумов:
Произведем вычисления максимумов функции. Получим, что
Второй признак экстремума функции
Для начала находим область определения. Получаем, что
Необходимо продифференцировать функцию, после чего получим
Третье достаточное условие экстремума
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.
Общие сведения
Функция — величина, которая может принимать различные значения, определённые аргументом, то есть условием. Другими словами, значение параметра изменяется в зависимости от того, какой вид принимает связанный с ней определитель. Аргумент и функция — это переменные действительные числа.
Понятие можно описать как ответ на какой-либо вопрос. Например, если спросить, какого цвета маркер, можно ответить чёрный. Так вот цвет фломастера — это аргумент, а ответ — функция. При этом двух разных ответов на вопрос быть не может, а вот ситуация, наоборот, вполне возможна. Чёрным может быть не только маркер, но и рубашка. Значит, параметр может принимать одно и то же значение при разных величинах аргумента.
Традиционный способ описания параметра заключается в составлении уравнения. С правой стороны в нём стоит выражение, которое показывает зависимость чисел, а слева — обозначение функции. Принято зависимое значение обозначать буквой игрек, а определяющее изменение символом икс. Например, y = x + 1. В этом равенстве справа находится сумма, которая показывает, что функция всегда будет больше на единицу, чем аргумент.
Уравнение в математике можно изобразить и графиком. Для этого используют координатную плоскость, на которой откладывают значения переменных. Выполняют рисунок, руководствуясь свойствами функций:
Ось икс называют абсциссой, а игрек — ординатой. Каждая точка на рисунке, соответствующая уравнению, определяется своей координатой. Визуально по графику исследовать поведение зависимости довольно удобно.
Характер зависимости
Для изучения поведения функции необходимо определить промежутки, на которых график уравнения возрастает или убывает. При этом равенство их может и вовсе не содержать или, наоборот, иметь довольно много. Переход из одного состояния в другое характеризуется точкой экстремума.
В математике она обозначает значение, соответствующее минимальным и максимальным координатам. При достижении наибольшего значения функции экстремум называют точкой максимума, а при соответствии наименьшей величине — точкой минимума. Понятие может быть применено как ко всему графику, так и выделенному на нём интервалу.
Существуют 2 правила, определяющих поведение уравнения:
Если уравнение описывается графиком непрерывным и определённым в конечных точках интервала возрастания и спадания, то есть координатами (a, b), они будут включены в промежуток роста и снижения. Это утверждение не противоречит определениям.
Когда наибольшее или минимальное значение, определённое на множестве M и принимающее вещественные значения, достигает того, что числа других функций с той же областью определения подчинены конкретным ограничительным правилам, говорят об условном экстремуме. Если же таких дополнительных условий нет, величина безусловная.
Точка называется локальным максимумом, если выполняется условие x ≠ x0, где икс принадлежит окрестности (x0−δ, x0+δ), и справедливо неравенство f (x) ≤ f (x0). Если же верно неравенство f (x) > f (x0) — локальным минимумом.
Условия появления экстремума
На самом деле каждая стационарная точка может быть возможным экстремумом, чтобы установить, так ли это, нужно проводить ряд исследований. Всего существует 3 достаточных условия. Если они выполняются, можно утверждать об изменении поведения функции в этой точке:
Для неравенства, у которого n ≥ 1 функция имеет производную некого порядка n в произвольной точке окрестности m, а в самой координате результатом дифференцирования является n + 1, причём справедливо равенство f / (m) = f n (m) ≠ 0, в m будет находиться локальный экстремум.
Из этих признаков следует важное правило, что если имеется непрерывная функция со стационарной точкой, в которой при взятии производной значение изменит знак, это и будет означать экстремум. Чтобы верно определить, до какой координаты функция убывает, а до какой возрастает, можно воспользоваться нахождением точки перехода. Для этого нужно выполнить следующие действия:
Иными словами, делается предположение, что на каком-то интервале (a, b) существует конечное число точек. Производная f (x) в них обращается в 0. Если принять, что это точки x1, x2… xn, то, согласно предположению f / (x), не изменит свой знак на интервалах: (a1x); (x1, x2); (xn, b). Отсюда следует, что при помощи первого признака может быть решён вопрос о существовании экстремума в этих точках.
Решение задач
В учебниках по математике после теоретического изложения материала ученикам предлагается самостоятельно решить ряд примеров. Этот навык помогает научиться применять полученные знания на практике и лучше усвоить тему.Вот некоторые из таких заданий, предназначенные для решения учениками девятого класса средней школы: