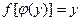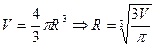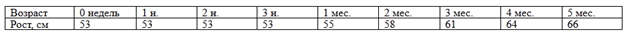Что такое функциональная зависимость в алгебре

Простейшие функциональные зависимости

Лекция 3. Общие понятия и определения. Классификация функций. Предел функции. Бесконечно малые и бесконечно большие функции. Основные теоремы о бесконечно малых функциях.

Функция

При решении различных задач обычно приходится иметь дело с постоянными и переменными величинами.

Определение

Постоянной величиной называется величина, сохраняющая одно и тоже значение или вообще или в данном процессе: в последнем случае она называется параметром.

Переменной величиной называется величина, которая может принимать различные числовые значения.

Понятие функции

При изучении различных явлений обычно имеем дело с совокупностью переменных величин, которые связаны между собой так, что значения одних величин (независимые переменные) полностью определяют значения других (зависимые переменные и функции).

Определение

Переменная величина y называется функцией (однозначной) от переменной величины x, если они связаны между собой так, что каждому рассматриваемому значению x соответствует единственное вполне определенное значение величины y (сформулировал Н.И.Лобачевский).

x – независимая переменная или аргумент;

y – зависимая переменная (функция);

f – характеристика функции.

Совокупность всех значений независимой переменной, для которых функция определена, называется областью определения или областью существования этой функции. Областью определения функции может быть: отрезок, полуинтервал, интервал, вся числовая ось.

Каждому значению радиуса соответствует значение площади круга. Площадь – функция от радиуса, определенная в бесконечном интервале

2. Функция (2). Функция определена при

Для наглядного представления поведения функции строят график функции.

Определение

Графиком функции y=f(x) называется множество точек M(x,y) плоскости OXY, координаты которых связаны данной функциональной зависимостью. Или график функции – это линия, уравнением которой служит равенство, определяющее функцию.

Например, график функции (2) – полуокружность радиуса 2 с центром в начале координат.

Простейшие функциональные зависимости

Рассмотрим несколько простейших функциональных зависимостей

Определение

Две переменные величины называются прямо пропорциональными, если при изменении одной из них в некотором отношении, другая изменяется в том же соотношении.

y=kx, где k – коэффициент пропорциональности.

Определение

Две переменные величины связаны линейной зависимостью, если , где — некоторые постоянные величины.

Определение

Две переменные величины называются обратно пропорциональными, если при изменении одной из них в некотором отношении, другая изменяется в обратном отношении.

Квадратичная зависимость в простейшем случае имеет вид , где k – некоторая постоянная величина. График функции – парабола.

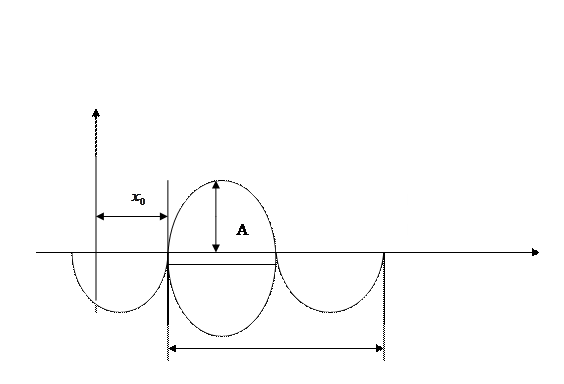
При изучении периодических явлений важную роль играет синусоидальная зависимость

— функция называется гармоникой.

— частота;

— начальная фаза.

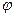
Функция периодическая с периодом 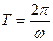. Значения функции в точках x и x+T, отличающихся на период, одинаковы.

Функцию можно привести к виду , где . Отсюда получаем, что графиком гармоники является деформированная синусоида с амплитудой A периодом T, сдвинутая по оси ОХ на величину

Способы задания функции

Обычно рассматривают три способа задания функции: аналитический, табличный, графический.

Если функция выражена при помощи формулы, то она задана аналитически.

Например

Если функция y=f(x) задана формулой, то ее характеристика f обозначает ту совокупность действий, которую нужно в определенном порядке произвести над значением аргумента x, чтобы получить соответствующее значение функции.

Пример 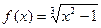. Выполняется три действия над значением аргумента.

Этот способ устанавливает соответствие между переменными с помощью таблицы. Зная аналитическое выражение функции, можно представить эту функцию для интересующих нас значений аргумента при помощи таблицы.

Можно ли от табличного задания функции перейти к аналитическому выражению?

Заметим, что таблица дает не все значения функции, причем промежуточные значения функции могут быть найдены лишь приближенно. Это, так называемое интерполирование функции. Поэтому, в общем случае найти точное аналитическое выражение функции по табличным данным нельзя. Однако всегда можно построить формулу, и при том не одну, которая для значений аргумента, имеющихся в таблице, будет давать соответствующие табличные значения функции. Такого рода формула называется интерполяционной.

Аналитический и табличный способы не дают наглядного представления о функции.

Этого недостатка лишен графический способ задания функции y=f(x), когда соответствие между аргументом x и функцией y устанавливается с помощью графика.

Понятие неявной функции

Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной.

Функция y от аргумента x называется неявной, если она задана уравнением

F(x,y)=0 (1) неразрешенным относительно зависимой переменной.

Пример.

Понятие обратной функции

Пусть задана функция y=f(x) (1). Задавая значения аргумента х, получаем значения функции y.

Можно, считая y аргументом, а х – функцией, задавать значения y и получать значения x. В таком случае уравнение (1) будет определять x, как неявную функцию от y. Эта последняя функция называется обратной по отношению к данной функции y.

Предполагая, что уравнение (1) разрешено относительно x, получаем явное выражение обратной функции

(2), где функция для всех допустимых значений y удовлетворяет условию

Пример

Обратная функция однозначной функции может быть многозначной, то есть данному значению y может соответствовать несколько значений 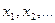обратной функции .

Например, тригонометрические функции и обратные тригонометрические функции. Или

— двузначная.

Источник

Что такое функциональная зависимость в алгебре

Записывают: у = f (х). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными х и у; f (х) есть значение функции, соответствующее значению аргумента х. Говорят также, что f (х) есть значение функции в точке х. Все значения, которые принимает независимая переменная, образуют область определения функции. Все значения, которые принимает функция f (х) (при х, принадлежащих области ее определения), образуют область значений функции.

Способы задания функции

Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х),

Пусть функция задана аналитически формулой у = f (х). Если на координатной плоскости отметить все точки, обладающие следующим свойством: абсцисса точки принадлежит области определения функции, а ордината равна соответствующему значению функции, то множество точек (х; f (x)) есть график функции. В физике и технике функции нередко задаются графически, причем иногда гарфик является единственным доступным средством задания функции. Чаще всего это бывает при употреблении самопишущих приборов, автоматически записывающих изменение одной величины в зависимости от изменения другой. В результате на ленте прибора получается линия, графически задающая регистрируемую прибором функцию.

Также функцию можно задать таблично. Рассмотрим примеры функциональной зависимости в реальной жизни.

Таблицей заданы данный о росте ребенка в течении первых 5 месяцев жизни:

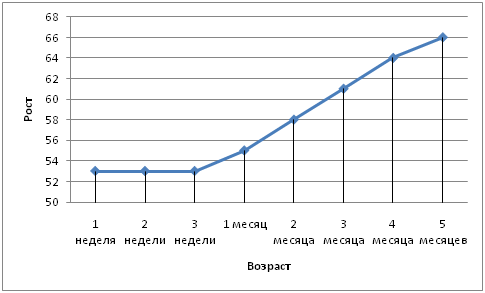
Имея таблицу значений функциональной зависимости роста от возраста, можно по точкам построить график:

Вот яркий пример функции, заданной графически. На графике можно увидеть максимум и минимум, фрагменты линейной функции, сглаживание линий и т.д.

Суть электрографии заключается в том, чтобы зарегистрировать разности потенциала во времени. Кривая, которая показывает нам эти изменения и есть кардиограмма. Прибор, который записывает эту кривую, именуется электрокардиографом. Кардиограмма сердца показывает возбуждение сердца и его сокращение. Во время снятия кардиограммы к телу человека прикрепляются специальные электроды, благодаря которым аппарат и получает необходимые данные.

Суть обработки сигналов данного исследования заключается в том, чтобы диагностировать имеющиеся проблемы в работе сердечных мышц, используя при этом различные аналитические методы.

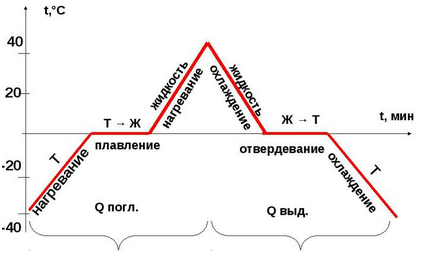
Переход вещества из твердого состояние в жидкое называется плавлением. Для того чтобы тело начало плавиться, его необходимо нагреть до определенной температуры. Температура, при которой вещество плавится, называют температурой плавления вещества.

Каждое вещество имеет свою температуру плавления. У каких-то тел она очень низкая, например, у льда. А у каких-то тел температура плавления очень высокая, например, железо. Плавление кристаллического тела это сложный процесс.

На рисунке представлен известный из курса физики график плавления льда.

Рассмотрим задачу

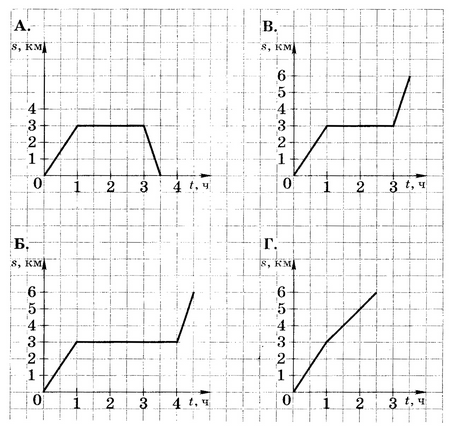
Туристы отправились с турбазы на озеро, провели там 2 часа и вернулись обратно. Выберите график, описывающий зависимость пройденного расстояния от времени:

Верным будет ответ А., т.к. в течении двух часов туристы находились на озере, добравшись до него, а затем снова вернулись в лагерь, т.е. в нулевую точку отсчета.

Источник

Функция. Аргумент. Прямая и обратная зависимость

Содержание

Вокруг нас происходит множество событий или процессов, которые можно измерить. При этом величина одних зависит от величины каких-либо других.

Так, например, от того, сколько мы испишем страниц в тетради, зависит количество оставшихся в стержне чернил. Чем больше кружек наполнено компотом, тем меньше его останется в кастрюле. Чем больше мама оставит денег на обеды, тем больше можно на них купить мороженого. А чем сильнее велосипедист крутит педали, тем больше километров он проедет. Придумайте свои примеры?

В наших описанных выше примерах первые два имеют обратную зависимость, то есть при увеличении одной величины (количество страниц и кружек в наших случаях), уменьшается вторая (количество чернил и компота в кастрюле).

Обратная зависимость

Примеры с велосипедистом и мороженым имеют прямую зависимость, то есть при увеличении одной величины (скорость движения педалями и количество оставленных мамой денег) увеличивается и другая (пройденное расстояние и количество мороженого).

Прямая пропорциональность

Зависимость, которая показывает как одна величина связана с другой величиной, как раз и называется функцией.

Аргумент и функция

Зависимые и независимые переменные могут обозначаться и любыми другими буквами (латинскими или греческими).

Примеры аргумента и функции

Запись функции

Слово «функция» произошло от латинского слова functio – исполнение, осуществление. Это одно из главных понятий в математике, показывающее зависимость одних переменных величин от других. Понятие «величина» в данном случае может включать в себя совершенно любое число.

Переменные могут принимать как положительные, так и отрицательные значения.

Источник

Функциональные зависимости отношений и математическое понятие функциональной зависимости

Функциональная зависимость атрибутов отношения напоминает понятие функциональной зависимости в математике. Но это не одно и то же. Для сравнения напомним математическое понятие функциональной зависимости:

— множество (область определения),

— множество (множество значений),

— правило, согласно которому каждому элементу ставится в соответствие один и только один элемент (правило функциональной зависимости).

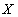
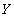
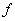
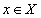
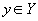
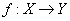
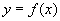
Функциональная зависимость обычно обозначается как или .

Функциональная зависимость атрибутов отношения тоже напоминает это определение. Действительно:

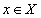
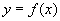
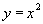
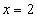
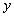
Отличие от математического понятия отношения состоит в том, что, если рассматривать математическое понятие функции, то для фиксированного значения соответствующее значение функции всегда одно и то же. Например, если задана функция , то для значения соответствующее значение всегда будет равно 4. В противоположность этому в отношениях значение зависимого атрибута может принимать различные значения в различных состояниях базы данных. Например, атрибут ФАМ функционально зависит от атрибута Н_СОТР. Предположим, что сейчас сотрудник с табельным номером 1 имеет фамилию Иванов, т.е. при значении детерминанта равного 1, значение зависимого аргумента равно «Иванов». Но сотрудник может сменить фамилию, например на «Сидоров». Теперь при том же значении детерминанта, равного 1, значение зависимого аргумента равно «Сидоров».

Таким образом, понятие функциональной зависимости атрибутов нельзя считать полностью эквивалентным математическому понятию функциональной зависимости, т.к. значение этой зависимости различны при разных состояниях отношения, и, самое главное, эти значения могут меняться непредсказуемо.

Функциональная зависимость атрибутов утверждает лишь то, что для каждого конкретного состояния базы данных по значению одного атрибута (детерминанта) можно однозначно определить значение другого атрибута (зависимой части). Но конкретные значение зависимой части могут быть различны в различных состояниях базы данных.

2НФ (Вторая Нормальная Форма)

Определение 3. Отношение 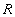находится во второй нормальной форме (2НФ) тогда и только тогда, когда отношение находится в 1НФ и нет неключевых атрибутов, зависящих от части сложного ключа. (Неключевой атрибут – это атрибут, не входящий в состав никакого потенциального ключа).

Замечание. Если потенциальный ключ отношения является простым, то отношение автоматически находится в 2НФ.

Отношение СОТРУДНИКИ_ОТДЕЛЫ_ПРОЕКТЫ не находится в 2НФ, т.к. есть атрибуты, зависящие от части сложного ключа:

Зависимость атрибутов, характеризующих сотрудника от табельного номера сотрудника является зависимостью от части сложного ключа:

Н_СОТР 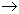ФАМ

Н_СОТР 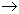Н_ОТД

Н_СОТР 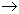ТЕЛ

Зависимость наименования проекта от номера проекта является зависимостью от части сложного ключа:

Н_ПРО 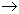ПРОЕКТ

Для того, чтобы устранить зависимость атрибутов от части сложного ключа, нужно произвести декомпозицию отношения на несколько отношений. При этом те атрибуты, которые зависят от части сложного ключа, выносятся в отдельное отношение.

Отношение СОТРУДНИКИ_ОТДЕЛЫ (Н_СОТР, ФАМ, Н_ОТД, ТЕЛ):

Зависимость атрибутов, характеризующих сотрудника от табельного номера сотрудника:

Н_СОТР 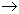ФАМ

Н_СОТР 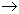Н_ОТД

Н_СОТР 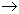ТЕЛ

Зависимость номера телефона от номера отдела:

Н_ОТД ТЕЛ

Источник

Что такое функциональная зависимость в алгебре

Основные понятия.

Функция (или Функциональная зависимость) – это зависимость переменной y от переменной x. Это такая зависимость, при которой каждому значению переменной x соответствует только одно значение переменной y.

Переменную x называют независимой переменной или аргументом.

Переменную y называют зависимой переменной или функцией от переменной x.

Значение независимой переменной называют абсциссой (горизонтальная плоскость графика).

Соответствующее значение зависимой переменной называется ординатой (вертикальная плоскость графика).

Совокупность значений независимой переменной называется областью определения функции.

Совокупность значений зависимой переменной называют областью значений функции.

График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

Значения аргумента, при которых функция обращается в нуль, называют нулями функции.

То есть в этой точке кривая имеет координаты (-2;0):

Этот аргумент и называется нулем рассматриваемой функции.

Если кривая на оси координат возрастает, то это означает, что с увеличением значения аргумента увеличивается и значение функции. Такая функция называется возрастающей.

Если кривая убывает, то это означает, что с увеличением значения аргумента значение функции убывает. Такая функция называется убывающей.

Виды функций.

Существует несколько основных видов функций:

Графики функций.

Графиком линейной функции y = kx + b является прямая.

Графиком прямой пропорциональности y = kx является прямая, проходящая через начало координат.

k
Графиком обратной пропорциональности y = — является гипербола.
x

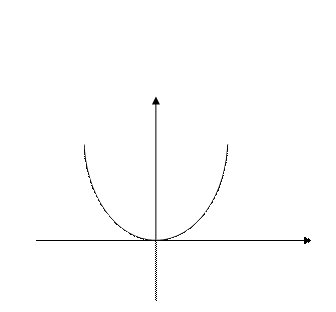
Графиком квадратичной функции y = x 2 является парабола.
Если х = 0, то у = 0.
Если х ≠ 0, то у > 0.

Подробнее о приведенных и других функциях – в следующих разделах.

Источник