Что такое фрактал в математике

Что такое фрактал в математике

В этой статье приведены примеры расчета и построения графической интерпретации некоторых алгебраических и геометрических фракталов.

Фракталы можно разделить на несколько видов:

Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.

Некоторые примеры алгебраических и геометрических фракталов

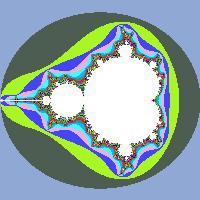
Фрактал Мандельброта

Рассмотрим последовательность комплексных чисел:

\[z_ = z_k^2 + c, k = 0, 1, 2, \dots, z_0 = c\]

Множество точек c, для которого эта последовательность не расходится, называется множеством Мандельброта. Для построения его графической интерпретации нужно определить исходные данные:

Если точка \(z_k\) вышла за пределы круга радиуса \(r_\min\) при \(k \lt k_\max\), то процесс вычисления останавливается.

Построение: для каждой точки \(c_ \in C (i = \overline<1, n>, j = \overline<1, m>, c_x \in [-2; 1], c_y \in [-2; 1,5])\) запустим итерационный процесс:

где \(k = 0, 1, 2, \dots, k_\max\) и \(\sqrt \leqslant r_\min\).

Если представить множество в общем виде:

то, изменяя значение N, можно получать симметричные фрактальные множества. Например, для \(N = 4\) и \(N = 7\):

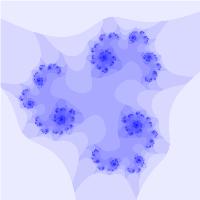
Фрактал Жюлиа

Рассмотрим ту же последовательность комплексных чисел, что и для множества Мандельброта:

\[z_ = z_k^2 + c, k = 0, 1, 2, \dots\]

Исходные данные, этапы построения и условия остановки – те же, что и для фрактала Мандельброта, за исключением:

Рассматривая множество в общем виде: \(z_ = z_k^N + c\) и изменяя N и с, можно получать разнообразные фрактальные множества:

Бассейны Ньютона

Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости.

Общая формула метода Ньютона имеет вид:

При выборе различных \(z_0\) процесс будет сходиться к различным корням (областям притяжения). Границы этих областей имеют фрактальную структуру.

Подставив \(p(z)\) в формулу метода, получим итерационную формулу для построения фрактала:

Итерационный процесс останавливается при:

\[\left| z_^3 \right| \leqslant r_\min\]

Для построения графической интерпретации также как и для фрактала Мандельброта, используется матрица, элементы которой равны номеру итерации, на которой остановился процесс.

Если записать формулу в общем виде:

то можно получить изображения фракталов более сложной формы:

L-системы

В 1968 году венгерский биолог Аристид Линденмайер предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена для моделирования сложных ветвящихся структур (разнообразных растений). Эта модель получила название Lindenmayer System (Система Линденмайера или L-система).

Рекурсивная природа L-систем позволяет строить с их помощью геометрические фрактальные изображения.

Правила применяются итеративно, начиная с аксиомы. За одну итерацию применяются одновременно все правила.

Например, L-система имеет вид:

Правила: \((A \rightarrow AB) (B \rightarrow BA)\)

После нескольких применений правил из аксиомы получаются строки:

Для построения графической интерпретации L-системы используется «черепашья графика», т.е. символам из V присваиваются команды управления некоторым простым интерпретатором («пройти вперед», «повернуться», и т. д.).

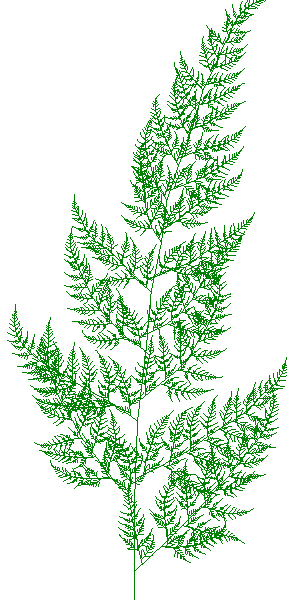
Лист папоротника

Существует несколько способов построения этого фрактала.

1) Построение с помощью системы итерируемых функций (IFS)

Производится 20 итераций функции \(f(x, y)\). Каждое новое значение получается из предыдущего в зависимости от случайного числа, т. е. вычисляется с использованием таблицы распределения:

После выполнения всех итераций точка рисуется на экране.

Начальные значения x и y могут быть константами (желательно не большими, чем 1) или их можно выбирать случайным образом на отрезке \([0;1]\).

2) Рекурсивное построение

Для построения используется процедура (псевдокод):

Рекомендуемые значения углов и коэффициентов: \(\phi_0 = 14,9^<\circ>, \phi_1 = 37,7^<\circ>, \phi_2 = 36,8^<\circ>, \phi_3 = 17,6^<\circ>, k_1 = 0,0483, k_2 = 0,162, m_1 = 0,371, m_2 = 0,336, m_3 = 0,849\).

Для получения более реалистичного изображения можно использовать метод управляемой случайности. Метод заключается в том, что в процесс сознательно вносятся помехи. В алгоритме построения ветви папоротника можно внести изменения в углы ветвления φ1, φ2, φ3.

Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале \((-10^<\circ>; 10^<\circ>)\), можно получить изображения:

Литература:

Программы

Здесь приведены ссылки на программы, с помощью которых были созданы иллюстрации для этой статьи.

Источник

Что такое фракталы: красота математики и бесконечность

Фракталы известны уже век, хорошо изучены и имеют многочисленные приложения в жизни. Однако в основе этого явления лежит очень простая идея: бесконечное по красоте и разнообразию множество фигур можно получить из относительно простых конструкций при помощи всего двух операций – копирования и масштабирования.

Что общего у дерева, берега моря, облака или кровеносных сосудов у нас в руке? На первый взгляд может показаться, что все эти объекты ничто не объединяет. Однако на самом деле существует одно свойство структуры, присущее всем перечисленным предметам: они самоподобны. От ветки, как и от ствола дерева, отходят отростки поменьше, от них — еще меньшие, и т. д., то есть ветка подобна всему дереву.

Подобным же образом устроена и кровеносная система: от артерий отходят артериолы, а от них — мельчайшие капилляры, по которым кислород поступает в органы и ткани. Посмотрим на космические снимки морского побережья: мы увидим заливы и полуострова; взглянем на него же, но с высоты птичьего полета: нам будут видны бухты и мысы; теперь представим себе, что мы стоим на пляже и смотрим себе под ноги: всегда найдутся камешки, которые дальше выдаются в воду, чем остальные.

То есть береговая линия при увеличении масштаба остается похожей на саму себя. Это свойство объектов американский (правда, выросший во Франции) математик Бенуа Мандельброт назвал фрактальностью, а сами такие объекты — фракталами (от латинского fractus — изломанный).

Что такое фрактал?

Геометрия и алгебра

Изучение фракталов на рубеже XIX и XX веков носило скорее эпизодический, нежели систематический характер, потому что раньше математики в основном изучали «хорошие» объекты, которые поддавались исследованию при помощи общих методов и теорий. В 1872 году немецкий математик Карл Вейерштрасс строит пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия.

Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».

Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал — С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.

Другой класс — динамические (алгебраические) фракталы, к которым относится и множество Мандельброта. Первые исследования в этом направлении начались в начале XX века и связаны с именами французских математиков Гастона Жулиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный мемуар Жулиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жулиа — целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно.

Несмотря на то что это работа прославила Жулиа среди математиков того времени, о ней довольно быстро забыли. Вновь внимание к ней обратилось лишь полвека спустя с появлением компьютеров: именно они сделали видимыми богатство и красоту мира фракталов.

Фрактальные размерности

Как известно, размерность (число измерений) геометрической фигуры – это число координат, необходимых для определения положения лежащей на этой фигуре точки.

Например, положение точки на кривой определяется одной координатой, на поверхности (не обязательно плоскости) двумя координатами, в трёхмерном пространстве тремя координатами.

С более общей математической точки зрения, можно определить размерность таким образом: увеличение линейных размеров, скажем, в два раза, для одномерных (с топологической точки зрения) объектов (отрезок) приводит к увеличению размера (длины) в два раза, для двумерных (квадрат) такое же увеличение линейных размеров приводит к увеличению размера (площади) в 4 раза, для трехмерных (куб) – в 8 раз. То есть «реальную» (т.н. Хаусдорфову) размерность можно подсчитать в виде отношения логарифма увеличения «размера» объекта к логарифму увеличения его линейного размера. То есть для отрезка D=log(2)/log(2)=1, для плоскости D=log(4)/log(2)=2, для объема D=log(8)/log(2)=3.

Подсчитаем теперь размерность кривой Коха, для построения которой единичный отрезок делят на три равные части и заменяют средний интервал равносторонним треугольником без этого сегмента. При увеличении линейных размеров минимального отрезка в три раза длина кривой Коха возрастает в log(4)/log(3)

1,26. То есть размерность кривой Коха – дробная!

Наука и искусство

В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей. Благодаря иллюстрациям, полученным при помощи компьютера, и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике.

Их успех среди нематематиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения. Когда персональные компьютеры стали достаточно мощными, появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой теме.

Схема получения кривой Коха

Война и мир

Как уже отмечалось выше, один из природных объектов, имеющих фрактальные свойства, — это береговая линия. С ним, а точнее, с попыткой измерить его длину, связана одна интересная история, которая легла в основу научной статьи Мандельброта, а также описана в его книге «Фрактальная геометрия природы».

Речь идет об эксперименте, который поставил Льюис Ричардсон — весьма талантливый и эксцентричный математик, физик и метеоролог. Одним из направлений его исследований была попытка найти математическое описание причин и вероятности возникновения вооруженного конфликта между двумя странами. В числе параметров, которые он учитывал, была протяженность общей границы двух враждующих стран. Когда он собирал данные для численных экспериментов, то обнаружил, что в разных источниках данные об общей границе Испании и Португалии сильно отличаются.

Это натолкнуло его на следующее открытие: длина границ страны зависит от линейки, которой мы их измеряем. Чем меньше масштаб, тем длиннее получается граница. Это происходит из-за того, что при большем увеличении становится возможным учитывать все новые и новые изгибы берега, которые раньше игнорировались из-за грубости измерений. И если при каждом увеличении масштаба будут открываться ранее не учтенные изгибы линий, то получится, что длина границ бесконечна! Правда, на самом деле этого не происходит — у точности наших измерений есть конечный предел. Этот парадокс называется эффектом Ричардсона.

Конструктивные (геометрические) фракталы

Алгоритм построения конструктивного фрактала в общем случае таков. Прежде всего нам нужны две подходящие геометрические фигуры, назовем их основой и фрагментом. На первом этапе изображается основа будущего фрактала. Затем некоторые ее части заменяются фрагментом, взятым в подходящем масштабе, — это первая итерация построения. Затем у полученной фигуры снова некоторые части меняются на фигуры, подобные фрагменту, и т. д. Если продолжить этот процесс до бесконечности, то в пределе получится фрактал.

Рассмотрим этот процесс на примере кривой Коха. За основу кривой Коха можно взять любую кривую (для «снежинки Коха» это треугольник). Но мы ограничимся простейшим случаем — отрезком. Фрагмент — ломаная, изображенная сверху на рисунке. После первой итерации алгоритма в данном случае исходный отрезок совпадет с фрагментом, затем каждый из составляющих его отрезков сам заменится на ломаную, подобную фрагменту, и т. д. На рисунке показаны первые четыре шага этого процесса.

Языком математики: динамические (алгебраические) фракталы

Комплексные числа

Таким образом, любая точка z комплексной плоскости имеет свой характер поведения при итерациях функции f (z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). Так вот, оказывается, что множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жулиа для функции f (z).

Семейство драконов

Варьируя основу и фрагмент, можно получить потрясающее разнообразие конструктивных фракталов.

Более того, подобные операции можно производить и в трехмерном пространстве. Примерами объемных фракталов могут служить «губка Менгера», «пирамида Серпинского» и другие.

К конструктивным фракталам относят и семейство драконов. Иногда их называют по имени первооткрывателей «драконами Хейвея-Хартера» (своей формой они напоминают китайских драконов). Существует несколько способов построения этой кривой. Самый простой и наглядный из них такой: нужно взять достаточно длинную полоску бумаги (чем тоньше бумага, тем лучше), и согнуть ее пополам. Затем снова согнуть ее вдвое в том же направлении, что и в первый раз.

После нескольких повторений (обычно через пять-шесть складываний полоска становится слишком толстой, чтобы ее можно было аккуратно гнуть дальше) нужно разогнуть полоску обратно, причем стараться, чтобы в местах сгибов образовались углы в 90˚. Тогда в профиль получится кривая дракона. Разумеется, это будет лишь приближение, как и все наши попытки изобразить фрактальные объекты. Компьютер позволяет изобразить гораздо больше шагов этого процесса, и в результате получается очень красивая фигура.

Множество Мандельброта строится несколько иначе. Рассмотрим функцию fc (z) = z^2+с, где c — комплексное число. Построим последовательность этой функции с z0=0, в зависимости от параметра с она может расходиться к бесконечности или оставаться ограниченной. При этом все значения с, при которых эта последовательность ограничена, как раз и образуют множество Мандельброта. Оно было детально изучено самим Мандельбротом и другими математиками, которые открыли немало интересных свойств этого множества.

Видно, что определения множеств Жулиа и Мандельброта похожи друг на друга. На самом деле эти два множества тесно связаны. А именно, множество Мандельброта — это все значения комплексного параметра c, при которых множество Жулиа fc (z) связно (множество называется связным, если его нельзя разбить на две непересекающиеся части, с некоторыми дополнительными условиями).

Фракталы и жизнь

В наши дни теория фракталов находит широкое применение в различных областях человеческой деятельности. Помимо чисто научного объекта для исследований и уже упоминавшейся фрактальной живописи, фракталы используются в теории информации для сжатия графических данных (здесь в основном применяется свойство самоподобия фракталов — ведь чтобы запомнить небольшой фрагмент рисунка и преобразования, с помощью которых можно получить остальные части, требуется гораздо меньше памяти, чем для хранения всего файла).

Добавляя в формулы, задающие фрактал, случайные возмущения, можно получить стохастические фракталы, которые весьма правдоподобно передают некоторые реальные объекты — элементы рельефа, поверхность водоемов, некоторые растения, что с успехом применяется в физике, географии и компьютерной графике для достижения большего сходства моделируемых предметов с настоящими. В радиоэлектронике выпускают антенны, имеющие фрактальную форму. Занимая мало места, они обеспечивают вполне качественный прием сигнала.

Экономисты используют фракталы для описания кривых колебания курсов валют (это свойство было открыто Мандельбротом). На этом мы завершим эту небольшую экскурсию в удивительный по красоте и разнообразию мир фракталов.

Источник

Теория фракталов

Еще в конце XIX — начале XX в. ученые математически описали необычные структуры, которые удалось изобразить много позже только с помощью компьютера. Это фракталы. Слово происходит от латинского fractus, одно из значений которого — «сломанный, разбитый». Широкую популярность фракталы обрели в 1983 г. после выхода книги Бенуа Мандельброта «Фрактальная геометрия природы».

Действительно, у многих структур имеется фундаментальное свойство, которое называется геометрической регулярностью. Оно известно как инвариантность по отношению к масштабу, или самоподобие. Когда рассматриваешь некоторые объекты в разных масштабах, то постоянно обнаруживаются одни и те же фундаментальные элементы. Эти закономерности повторяются и определяют дробную, или фрактальную, размерность структуры. Природные формы описываются фрактальной геометрией, вероятно, более изящно и точно, чем евклидовой.

Итак, фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.

В природе фракталов очень много. Возьмем, например, дерево, кровеносную систему, облако, берег моря. У них есть общее свойство — самоподобие. От ствола дерева отходят толстые ветки, от них — ветки потоньше и т.д. Фрагмент облака похож на большое облако. От артерий отходят артериолы, от них, в свою очередь, — капилляры. То есть ветка подобна всему дереву, а артериолы с капиллярами — всей кровеносной системе. То же самое происходит и с морским берегом. На космических снимках морского побережья видны полуострова и заливы, с высоты птичьего полета можно различить мысы и бухты, а если мы стоим на самом берегу, то видим уже мелкие неровности берега вплоть до камешков, которые выдаются в воду дальше, чем остальные. Таким образом, при увеличении масштаба неровная береговая линия остается неровной, похожей сама на себя.

В наши дни теория фракталов широко применяется в разных областях. Это фрактальная живопись: сегодня каждый может попробовать себя в ней, используя компьютер. Это теория информации, в которой свойство самоподобия фракталов используется для сжатия графических данных. Ведь для фрагмента рисунка требуется гораздо меньше памяти, чем для всего изображения. А восстановить целое можно из этого единственного фрагмента. Это география, где с помощью фрактальной геометрии можно создать весьма правдоподобные модели рельефа или поверхности водоемов. Это радиоэлектроника, где создаются антенны, обладающие фрактальной структурой. Они занимают меньше места, чем обычные, но обеспечивают качественный прием сигнала. Это экономика, где фрактальная математика описывает колебания курсов валют. Так что фракталы, можно сказать, вездесущи.

Бесконечна ли граница

Интересные результаты получаются и при измерении общих границ между двумя странами. Математик, физик и метеоролог Льюис Ричардсон обнаружил это, пытаясь дать математическое описание причин и вероятности войны между двумя государствами. Одним из параметров была протяженность общей границы. Собирая информацию, ученый изучал границы между всевозможными странами и обнаружил, что разные источники предоставляют различные данные об общей границе между Испанией и Португалией. Оказалось, что длина границ зависит от линейки, с помощью которой их измеряют. Чем крупнее масштаб, тем точнее измерение, тем больше ранее проигнорированных изгибов учитывается и тем длиннее граница! А если увеличивать масштаб бесконечно, то и граница окажется бесконечной. Хотя технически это невозможно — всякая точность измерения имеет свой предел. Этот парадокс носит название эффекта Ричардсона.

Источник

Что такое фракталы? Мир вокруг нас. Часть первая

«Вся сложность в простоте»

«. всё фрактально повторяется в этом материальном мире…»

«СОЗНАНИЕ И ЛИЧНОСТЬ. От заведомо мёртвого к вечно Живому»

Что такое фрактал

Что такое фрактал? Как устроен мир вокруг нас? Что лежит в основе всего? Почему наша Галактика по форме похожа на раковину Наутилуса, человеческий глаз на космическую туманность, а клетки мозга на всю нашу Вселенную?

Кому из вас не доводилось видеть похожие формы в живых и неживых объектах? Будто одна и та же формула, пронизывает всё вокруг.

Рис. 1. Фотография Вселенной, клетки мозга, рождение звезды, деление клетки, глаз человека и туманности

Схожие формы встречаются повсюду, от микро- до макромира: в минералах, растениях и животном мире, в структуре ДНК, в природных явлениях (циклоны, молнии, береговые линии), планетарных системах и звёздных скоплениях. Они присутствуют и в живых организмах.

Каковы закономерности и в чём причина такого сходства? Объяснением этому является фрактал. Фрактальность также прослеживается как в самом человеке, так и во взаимоотношениях в семье, коллективе и обществе в целом.

Рис. 2. Пример фракталов: клетки лука и эзоосмическая решётка

Фрактал (лат. «fractus» – дроблёный) – самоподобие (копирование) геометрических фигур, где каждый фрагмент дублируется в уменьшающемся масштабе. В природе это явление встречается очень часто.

Можно сказать, что фрактал – это узор, который повторяет сам себя в разных масштабах до бесконечно малого или/и бесконечно большого. Он рождается не просто повторением форм, а скорее повторением процесса, который применяется к форме. Бесконечная цепочка самопостроения.

В природе ярким примером такого узора является капуста сорта «Романеско».

Рис. 3. Пример фрактала в природе, капуста «Романеско»

История открытия фракталов

Опираясь на найденные интересные артефакты, мы видим, что знаниями о фракталах располагали люди ещё в древности. Их изображение мы находим на керамике Трипольской культуры (с 5450 по 2700 год. до н. э.), в очертаниях построения селений и городищ, архитектуре зданий. Более подробно об этом будет рассказано во второй части статьи.

На данный момент нам не известно, каким термином называли наши предки явление самоподобия объектов. Но точно можно сказать, что знания о фракталах входили в раздел «сакральной геометрии» прошлого. Понимание математической закономерности всего миропорядка было естественным ещё тысячелетия назад.

К примеру, выдающемуся зодчему Древнего Египта Имхотепу удалось возвести первую в той стране ступенчатую пирамиду – грандиозное фрактальное сооружение с чёткими математическими пропорциями. К слову сказать, группа близких Имхотепу людей называли Бога не иначе как Великим Зодчим Мироздания. А во времена существования ордена Тамплиеров по всей Европе получил широкое распространение готический стиль архитектуры – воплощение сакральной геометрии и фрактальных узоров в камне.

Однако, со временем учёные выбрали другой, материалистический путь развития науки, который увёл нас далеко от этих знаний, и божественные законы были забыты.

Как современники пришли к понятию «фрактал»

В области изучения фракталов ещё в конце ХIX – начале ХХ веков работали многие учёные: Пьер Фату, Жюль Анри Пуанкаре, Георг Кантор, Феликс Хаусдорф, Гастон Жюлиа. Они и заложили математическую базу для появления теории фракталов.

Появление вычислительных устройств позволило ускоренно проводить итерации (многократно повторяющийся процесс вычисления) и визуализировать формулы. А сама идея ввести формулу Гастона Жюлиа в компьютер и с его помощью произвести громоздкие расчеты пришла в голову Мандельброту приблизительно в 1977 году. Раз за разом, меняя переменную C, он получал новые удивительные изображения. Таким образом, множества Жюлиа приобрели геометрические формы. (см. Множества Жюлиа). В 1980 г. программа отпечатала нечто похожее на кляксу. (см. фрактал Мандельброта). Это простое на первый взгляд изображение при приближении выявляет в себе новые и новые отображения множеств Жюлиа, которым нет предела.

Рис. 4. Изображения фракталов. Фрактал Мандельброта. Множество Жюлиа

Много современных учёных успешно работали в данном направлении. Заслуга Бенуа заключается в том, что он первым визуализировал уже имеющиеся формулы, показав всему миру их невероятную красоту, и дал ныне существующее название этому явлению.

Виды фракталов

Фракталы бывают разных видов, рассмотрим некоторые из них:

Геометрические виды фракталов являются самыми наглядными и простыми в строении. Увидеть их может любой человек. Множество таких фракталов можно нарисовать на обычном листке бумаги в клетку. Примером являются: Треугольник Серпинского, Снежинка Коха, Н-фрактал, Т-фрактал, Дракон, Кривая Леви, Дерево Пифагора.

Рис. 5. Примеры геометрических фракталов

Рассмотрим принцип построения фракталов на примере – «Снежинки Коха» (рис. 6).

Он строится путём многократного разделения отрезка линии на 3 равные части и замены средней части на 2 новых отрезка той же длины. Число сторон каждый раз учетверяется, вследствие чего становится бесконечно великим. Периметр снежинки имеет бесконечную длину, но площадь при этом конечна, так как фигура является замкнутой.

Рис. 6. Фрактал – «Снежинка Коха»

«Снежинка Коха» стала основой фрактальных антенн, которые мы используем в мобильных устройствах. Благодаря такой форме антенны имеют компактный размер с широким диапазоном действия.

Рис. 7. Примеры фрактальных антенн

По принципу построения интересен также «Треугольник Серпинского».

Возьмём равносторонний треугольник, отметим середины его сторон.

Соединим срединные точки прямыми линиями. Образовались 4 треугольника.

Центральный треугольник вынимаем и «выкидываем».

Теперь повторим эту операцию с каждым из вновь образовавшихся треугольников. И так до бесконечности.

Рис. 8. Построение треугольника Серпинского

Из этого примера легко увидеть, что количество треугольников увеличивается, и сумма их периметров (сумма сторон треугольников) стремится к бесконечности, а сумма площадей – к нулю.

Треугольник Серпинского имеет нулевую площадь. Разбирая способ построения, можно увидеть, что «вынимая» из треугольника всё наполнение после каждой итерации (повторение операции построения), мы постоянно уменьшаем его площадь и в результате сводим её к нулю.

Это самая крупная группа фракталов, которая базируется на основе разных алгебраических формул. Ярким примером является фрактал Мандельброта. В настоящее время их принято отображать в цвете. Получаются красивейшие необычные орнаменты, которые используют, например, в дизайне одежды.

Рис. 9. Изображения алгебраических фракталов

Не менее популярным является способ построения, основанный на комплексной динамике. В результате образуются фракталы, напоминающие живые организмы – биоморфы. (рис.10).

Рис. 10. Изображения фракталов – «биоморфы»

Строятся путём хаотического изменения некоторых параметров. При этом получаются объекты, очень похожие на природные. Фракталы данного вида широко применяются в киноиндустрии. С помощью компьютерной графики создаются искусственные горы, облака, поверхности моря, планеты, береговые линии, несимметричные деревья (рис.11). Также представителем данного вида является – «плазма» в природе:

Рис. 11. Стохастические фракталы

Концептуальные (социокультурные, непространственные) фракталы

Этот вид объединяет непространственные структуры, выходящие за рамки геометрической фрактальности. Принцип многоуровневого самоподобия заложен в культурных произведениях. В художественных текстах (стихах для детей, народных песнях, в музыкальных произведениях и сказках) часто встречается «рассказ в рассказе».

«У попа был двор, на дворе был кол, на колу мочало – не начать ли сказочку сначала. У попа был двор. »

Дедка, бабка, внучка.

Дедка, бабка, внучка, Жучка и т.д.

Фрактальность наблюдается в организации человеческих поселений (страна – город – квартал); в распределении общества на группы (народ – социокультурная группа – семья – человек). Сюда же отнесём фрактальность взаимоотношений, которые начинаются с самого человека. Меняется человек, его восприятие, внутреннее состояние – изменяется взаимоотношение в семье, коллективе, в итоге преобразуется всё общество. Прослеживается фрактальность в иерархических системах управления.

ФРАКТАЛЬНЫЕ ФОРМЫ В ПРИРОДЕ

Рис. 12. Фракталы в природе

Один из наглядных примеров фрактальной формы – береговые линии, которые отличаются друг от друга степенью своей изрезанности. Нет абсолютно одинаковых протоков, но их общие очертания как будто нарисованы одним лекалом. Эти очертания независимо от размера очень похожи. Маленький проток – это уменьшенная копия большого. Если увеличить верхний правый угол картинки, то она будет аналогична всей картине, изображенной на рисунке.

Рис. 13. Береговые линии

Растительный мир нашей зелёной планеты богат и разнообразен. На первый взгляд кажется, что в нём нет никакой закономерности: растения в лесу расположены беспорядочно, ветки с листьями на растениях тоже. Но возьмём, к примеру, дерево. Если рассматривать дерево поднимаясь от основания к вершине, то видно, как от ствола отходят большие ветви, на больших ветвях идёт такое же разветвление меньших веток, и дальше форма разветвления в любой части дерева будет повторяться, лишь уменьшаясь в размере к вершине. И зная принципы построения фракталов, изучив все закономерности расположения веток на вершине дерева, нетрудно догадаться, как выглядит это же дерево у своего основания.

Крона – это видимая часть дерева, которая является отражением корневой системы. А корни, в свою очередь, тоже имеют ярко выраженное фрактальное строение. (рис.14, б).

Рис. 14. Фракталы в природе на примере дерева

Самое интересное, что прожилки на листьях тоже образуют фрактальный рисунок, очень похожий на плоское миниатюрное дерево (рис.15). Нет листьев с одинаковым рисунком, так же как нет людей с одинаковым отпечатком пальца. Рисунок на каждом листе уникален.

Рис. 15. Фрактальность в листьях

Комнатное растение (королевская бегония) – яркий пример проявления фракталов в рисунке листьев. Маленькие листочки по форме и сочетанию цветов аналогичны большим, хотя и не являются их точной копией (рис.16).

Рис. 16. Листья королевской бегонии

Один из самых старых видов наземных растений – папоротники. Учёные полагают, что они существуют более 350 млн. лет. Строение листа этого растения очень похоже на компьютерный фрактал (рис.17). Именно это растение является ярким доказательством того, что чем древнее биологическая форма, тем чётче в ней прослеживается фрактал, то есть форма организма строится по простым правилам.

Рис. 17. Листья папоротников

Съедобные растения тоже несут в себе формы самоподобия. Красная капуста в продольном срезе имеет фрактальный рисунок. (рис.18)

Рис. 18. Фото разных сортов капусты

Казалось бы, тугой кочан капусты, а его красота может вдохновить даже художника. Белые утолщения центральных черенков плотно прижатых листьев образуют волшебный фрактальный лабиринт.

Лишайники так же как папоротники и мхи – это самые древние представители растительного мира, поэтому фракталы в них выражены особенно ярко. В их узлах содержатся те же фрактальные формы, что и по краям.

Фрактальность мироустройства, энергии.
Спираль как фрактал

Мир вокруг нас разнообразен. Многие объекты, существующие в природе, являются фракталами. В их основе лежит Божественная пропорция (число Фи) – это Золотое сечение и золотая спираль, благодаря которой мы воспринимаем красоту и гармонию природы, пропорциональность строения человека, древней архитектуры, классических произведений искусства.

Золотая спираль строится фрактальным способом: прямоугольник с золотой пропорцией. 1,618 (число Фи) разбивают на малые квадраты и проводят дугу. То есть в спиралях большая дуга переходит в подобную меньшую и т.д.

Рис. 20. Золотое сечение

Спираль сама по себе является фракталом, в котором каждый новый виток копирует предыдущие, но в новом масштабе. Прямая взаимосвязь между мироустройством микро- и макромира и формой спирали свидетельствует о фрактальном устройстве Вселенной.

Очень интересную информацию об этой взаимосвязи можно найти в книге «АллатРа» А. Новых:

«Ригден: Да, и это связано со структурированным ходом энергий, хранением информации и её обменом, в общем, с углублённой физикой. Если внимательно изучить этот вопрос, то можно понять, что многое в материальном мире располагается в форме спирали или совершает движение по спирали, начиная от микро- и заканчивая макрообъектами».

Здесь же мы читаем, что в мифологии древних народов основные моменты о сотворении мира схожи. Говорится, что из мира Бога появился Первичный Звук, который породил Вселенную в форме шара. А на его поверхности под действием сил Аллата (первичной энергии, порождающей жизненное движение) стала образовываться материя, которая благодаря тем же силам начала взаимодействовать между собой.

Весь мир создан по математическим пропорциям, и древние об этом знали и отразили своё знание в мифах о сотворении мира. Спираль и последовательность Фибоначчи – это тоже фракталы.

Понятие о двух противодействующих силах Вселенной запечатлены на артефактах разных культур и эпох символом спиралей, закрученных в разные стороны.

Рис. 20. Артефакты с символом спираль в культурах мира

Науке уже известно о спиральных структурах и спиралевидном движении энергии. В этом движении также обнаруживаются фрактальные свойства. Их можно увидеть в космосе, в теле человека, в растениях и природных явлениях (облака, циклоны, водовороты).

Физики наблюдали, как в турбулентных потоках большие вихри порождают вихри поменьше, а те ещё меньше, и такое деление спиралевидных энергий наблюдалось до тех видимых пределов, которые технически были доступны учёным.

Фрактальные свойства присутствуют в структуре и движении энергии электрического разряда, воды, в росте растений и т.д.

Чем полезны знания о фракталах

Понимание фрактального устройства упростило многие сферы научных исследований. Удивительная особенность фракталов – повторение аналогичного паттерна в разных масштабах – позволяет нам, изучив малую часть какого-либо события или явления, предполагать об устройстве целого.

Это свойство позволило более точно рассчитывать площади неровных изломанных поверхностей. Например географических, таких как береговые линии, облака, или биологических – внутренняя поверхность лёгких или нервных волокон.

Рис. 21. Изображение структуры лёгких

Фрактальное строение ландшафта позволило создавать 3D модели гор, облаков, берега, что широко используется в компьютерной графике кинематографа, программ обучения водителей, лётчиков, а также в компьютерных играх. По факту, это есть создание иллюзорной копии нашего мира (иллюзии внутри иллюзии).

В технической сфере мы научились производить фрактальные антенны, которые позволяют значительно уменьшить размеры конструкции, и расширить диапазон принимаемых частот без увеличения объёма и громоздкости.

Применение фрактального свойства в архитектуре привело к появлению новых необычных форм с увеличением прочности строений.

Знания о фракталах нашли применение во всех сферах жизни человека – в физике, экономике, культуре, биологии, геологии и т.д.

Но главное – это реальный шанс по-новому взглянуть на мироустройство, которое пронизано фракталами вдоль, поперёк и насквозь. Например, изучение галактики, позволило учёным приблизиться к пониманию о строении Вселенной и о параллельных мирах.

ЗАКЛЮЧЕНИЕ

Как видим, фракталы – это не нечто обособленное и непонятное. Они наполняют нашу жизнь. Знания о фрактальном построении мира имелись у людей издревле. Мы провели небольшое исследование и нашли интересные факты, связанные с древностью фракталов, способами их применения в архитектуре и проявлений как в самом человеке, так и в обществе.

Во второй части нас ждёт захватывающее путешествие в историю, архитектуру, музыку. У нас будет возможность понять, как изменения в неизмеримо малом могут привести к глобальным трансформациям. И что может сделать человек как единица общества, чтобы наступило золотое тысячелетие, о котором люди мечтают с давних пор.

Конец первой части

Участники МОД «АЛЛАТРА»

Список литературы:

Анастасия Новых «АллатРа» К: изд-во «АЛЛАТРА» 2013

Анастасия Новых «Сэнсэй IV»

Анастасия Новых «Сэнсэй-II»

АЛЛАТРА ТВ передача «СОЗНАНИЕ И ЛИЧНОСТЬ. От заведомо мёртвого к вечно Живому»

Статья «К ТИПОЛОГИИ ФРАКТАЛОВ В ТЕОРИИ КУЛЬТУРЫ»

Смирнова А. С., Готический стиль в архитектуре и психология. (Научные труды Института Непрерывного Профессионального Образования. №4/2014.

Деменок С., Просто фрактал. – СПб.: ООО «Страта», 2012.

Cтатья из Вестника Брестского гос. техн. унив-та. 2015 №1: Колосовская А.Н. Архитектурные сооружения духовно-рыцарский орденов.

Г.М. Вдовин Г.М., Трубецков Д.И., Столетие фрактальной геометрии: От Жюлиа и Фату через Хаусдорфа и Безиковича к Мандельброту. Саратовский национальный исследовательский государственный университет им. Н.Г. Чернышевского. Россия. 2020.

Федер Е., Фракталы. Перевод Ю.А.Данилова и А.Шукурова. М.: «Мир». 1991.

Источник