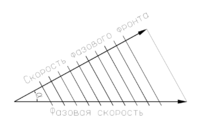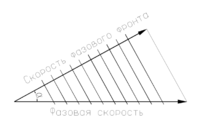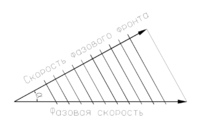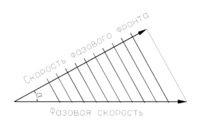
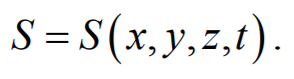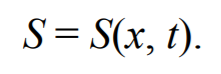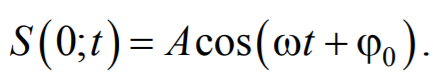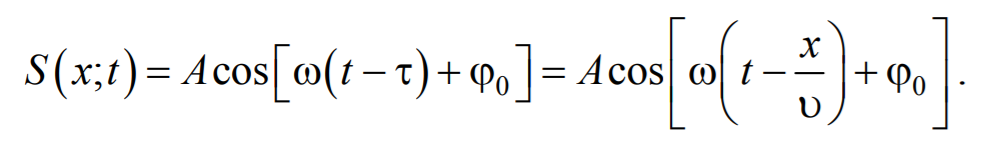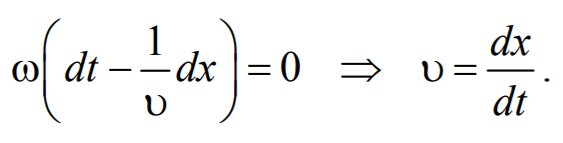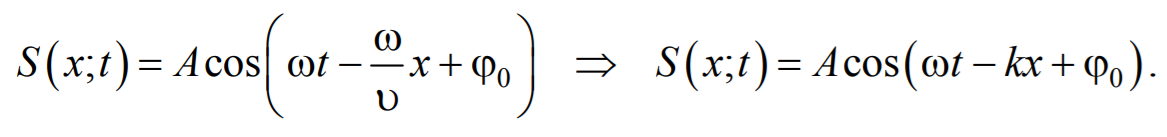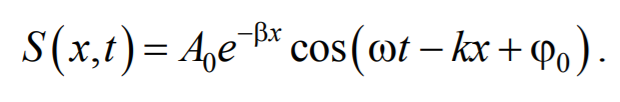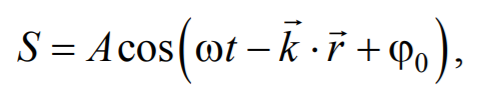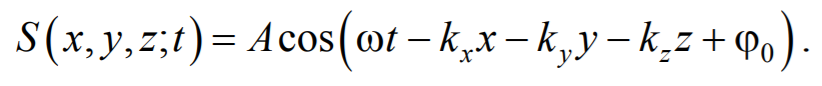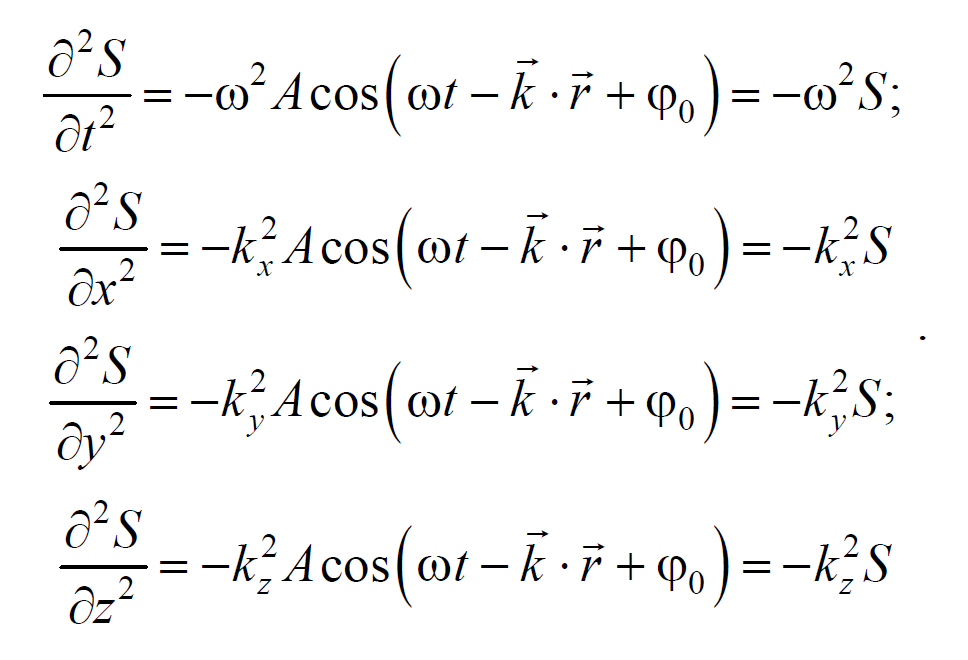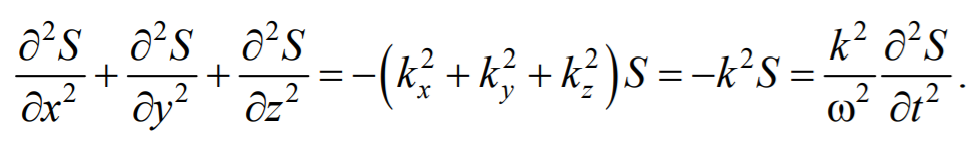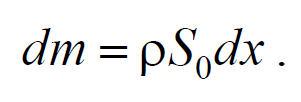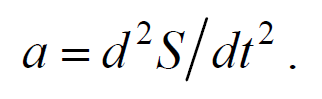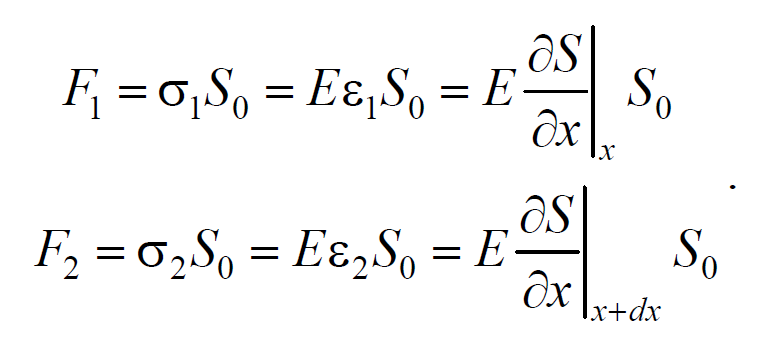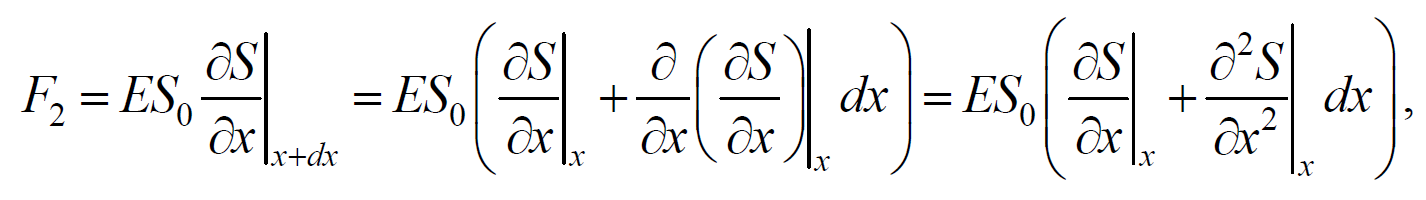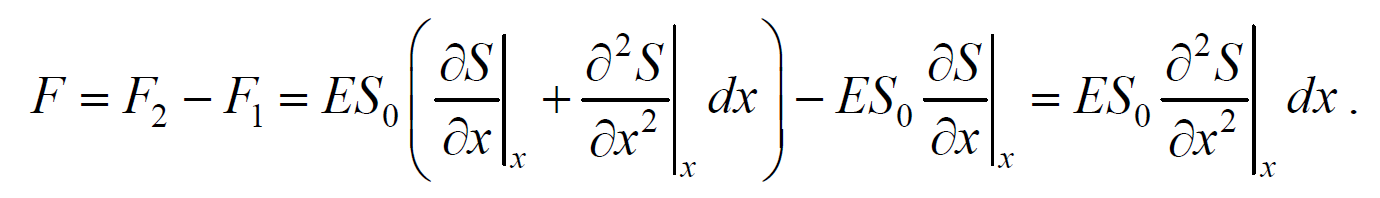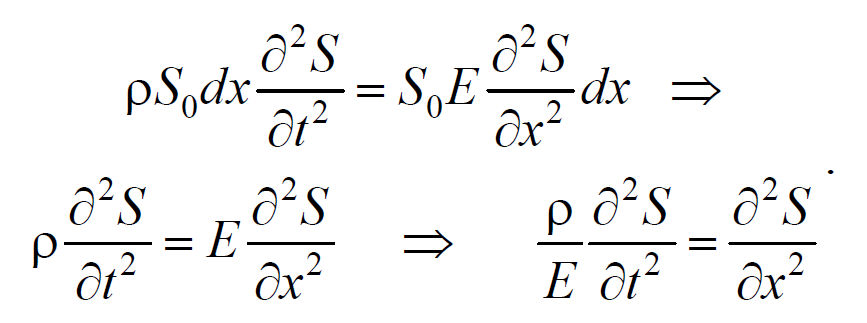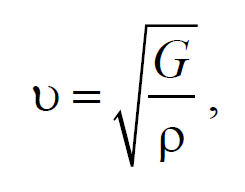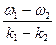Что такое фазовая скорость упругой волны

Лекция №9. Механические волны

6.1. Распространение колебаний в упругой среде

В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.

6.2. Уравнение плоской волны

Предположим, что колебания носят гармонический характер, а ось 0х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t

где А − амплитуда волны; ϕ₀ − начальная фаза волны (определяется выбором начал отсчета х и t ).

Тогда уравнение плоской волны будет иметь вид

6.3. Волновое уравнение

Уравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид

где r − радиус-вектор, точки волны; r =k× n − волновой вектор ; n − единичный вектор нормали к волновой поверхности

Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности называется.

Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3)

Сложив производные по координатам, и с учетом производной по времени, получим

6.4. Скорость распространения волн в различных средах

где Е − модуль Юнга среды.

Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема

где ρ − плотность недеформированной среды.

Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным

После разложения силы F₂ в ряд, получим

Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим

где Е − модуль Юнга.

Полученное уравнение определяет фазовую скорость продольных упругих волн.

Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид

Источник

Фазовая скорость

Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения, в пространстве вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой называют скорость, измеренную именно в этом направлении, если противное не указано явно (то есть если явно не указано направление, отличное от направления волнового вектора). Фазовая скорость по направлению волнового вектора совпадает со скоростью движения фазового фронта (поверхности постоянной фазы). Ее можно рассматривать при желании как векторную величину.

Наиболее употребительное обозначение: .

Строго говоря, понятие фазы применимо только при описании гармонических или монохроматических (то есть синусоидальных или являющихся мнимыми экспонентами ) волн, а также — приближенно — для волн близкой формы (например, почти монохроматических волновых пакетов) или легко сводящихся к синусоидальным (например, сферических волн вида ), или, что менее корректно, при описании периодических волн другой формы. Тем не менее, волну (практически) любой формы с помощью преобразования Фурье можно представить как сумму монохроматических волн, и тогда к каждой из этих волн понятие фазы и фазовой скорости применимо вполне строго (впрочем, тогда у каждой монохроматической волны в разложении будет, вообще говоря, своя фазовая скорость, не совпадающая с другими; только в частных случаях они могут все точно совпадать или быть близки).

Для описания волн, отличных от гармонических, (особенно для описания волновых пакетов), используют, кроме понятия фазовой скорости, понятие скорости групповой (описывающей движение не отдельного гребня в волновом пакете, а его огибающей, например, максимума огибающей).

Содержание

Формулы

Основная формула, определяющая фазовую скорость (монохроматической) волны в одномерном пространстве или фазовую скорость вдоль волнового вектора для волны в пространстве большей размерности:

которая является прямым следствием того факта, что фаза плоской волны в однородной среде есть

для одномерного случая

или для размерности, большей единицы.

Конкретное соотношение между ω и k — так называемый закон дисперсии для каждого конкретного типа волн получают обычно из дифференциального уравнения, описывающего данный тип волн, подставляя в него монохроматическую (чаще всего плоскую) волну [1]

В случае, когда фазовая скорость не зависит для данного типа волн от частоты или волнового числа (и направления волнового вектора), тогда и групповая скорость совпадает с нею.

Фазовая скорость электромагнитной волны

В вакууме для электромагнитной волны любой частоты (по крайней мере, в тех диапазонах частот и интенсивностей, которые исследованы) фазовая скорость, измеренная в направлении волнового вектора, всегда равна одной и той же величине — скорости света в вакууме, универсальной константе.

В средах закон дисперсии электромагнитных волн достаточно сложен (см. Дисперсия света), и фазовая скорость может заметно меняться.

Для волнового уравнения

Такой результат получается прямой подстановкой в это уравнение монохроматической волны вида и затем вычислением .

Этот результат верен не только для волнового уравнения на одномерном пространстве (мы его использовали выше лишь для краткости; всё остается совершенно аналогичным при любом количестве производных по координатам в правой части).

отличающееся только последним членом, дает при аналогичной подстановке

(Это выражение при ненулевых вещественных m всегда больше, чем C и может быть сколь угодно большим при k → 0.

Фазовая скорость как вектор

Но это, конечно, не мешает при желании ввести чисто формально вектор фазовой скорости, по определению совпадающий по направлению с волновым вектором, и с абсолютной величиной, равной фазовой скорости в этом направлении. Вопрос о том, корректно ли называть такой вектор вектором фазовой скорости, является чисто терминологическим (конвенциональным), фактом является лишь то, что его проекции на оси координат или компоненты по этим осям не будут соответствовать фазовой скорости вдоль этих направлений в соответствии с определением фазовой скорости по направлению, данным в начале статьи (и вообще с каким-то разумным определением, кроме чисто формального, описанного в данном абзаце).

Конкретно же, для случая плоской гармонической волны фазовую скорость вдоль волнового вектора можно выразить следующим образом:

, где k — волновое число, ω — угловая частота.

При этом, фазовая скорость вдоль направления, отклонённого от волнового вектора на угол , будет равна:

Может ли фазовая скорость превосходить скорость света

Фазовая скорость может превосходить скорость света в вакууме, и нередко ее превосходит. Это никак не противоречит известному принципу максимальности скорости света, необходимость которого возникает чтобы одновременно соблюдались принцип причинности (чтобы не возникало причинных парадоксов) и принцип относительности (лоренц-инвариантность).

Дело в том, что эти принципы накладывают ограничение только на скорость распространения таких физических объектов, посредством которых можно передать информацию. А фазовая скорость [5] не относится к скоростям таковых объектов. Чисто монохроматическая (синусоидальная) волна бесконечна в пространстве и во времени, не может никак измениться, чтобы передать информацию (если мы промодулируем волну, она перестанет быть монохроматической, а скорость распространения модуляции — не совпадает с фазовой скоростью, обычно совпадая со скоростью групповой для почти монохроматических волн).

Фазовая скорость по направлению, не совпадающему с волновым вектором

Поскольку фазовая скорость, измеренная вдоль произвольного направления, не совпадающего с волновым вектором и направлением распространения волны, не является скоростью движения «физического объекта», то есть, объекта, состояние которого в последующие моменты времени причинно обусловлено состоянием в предыдущие, а по сути характеризует просто состояние осциллирующего поля в искусственно выбранных точках, часто (а именно если выбрать достаточно большой угол с волновым вектором), фазовая скорость по данному направлению любой, даже сколь угодно медленной (как показано в параграфе выше), волны может превышать скорость света, стремясь к бесконечности при стремлении угла к прямому.

В частности, фазовая скорость света (или вообще любой бегущей электромагнитной волны) в вакууме, измеренная по любому направлению, не совпадающему с ее волновым вектором, всегда больше скорости света.

Но дело не ограничивается фазовой скоростью по произвольному направлению. Скорость света может быть превзойдена даже и фазовой скоростью, измеренной вдоль волнового вектора.

Фазовая скорость для квантовой частицы

Фазовая скорость квантовой волны, соответствующей любой массивной частицы (то есть частицы, имеющей массу больше нуля), всегда больше скорости света. Это легко видеть из формул , и , из чего , в то время как E для массивных частиц всегда больше p за счет массы (энергии покоя).

Этот на вид парадоксальный результат связан с тем, что «распространение» такой волны является иллюзией [6] в том смысле, что между разными частями волны нет причинной связи (состояние волны, продвинувшейся вправо не определяется тем, какой она была слева). В этом смысле ситуация аналогична ситуации с движущимся быстрее света зайчиком итп.

Источник

Фазовая скорость волны

Волновое уравнение. Волна на струне является поперечной волной: смещение частиц струны происходит поперек направления распространения волны. Это показано на рис. 1-24а. Волна распространяется в направлении оси 0x со скоростью с, смещение частиц струны происходит в направлении оси 0y со скоростью смещения частиц v_y.

Рассмотрим динамику движения элемента колеблющейся струны длиной dl при малых амплитудах колебаний элемента струны(малых колебаниях). На рис. 1-24б элемент dl представлен в крупном масштабе. Длина элемента определяется теоремой Пифагора:

dl = . (23)

Величина = tga, но при малых колебаниях угол a представляет малую величину, поэтому в (23) можно пренебречь ее квадратом. Таким образом, при малых колебаниях можно принять соотношение: dl = dx.

Выделенный элемент струны длиной dl и массой dm перемещается в направлении оси 0y (волна поперечная). Ускорение элемента a_y = . Если проекция результирующей силы натяжения в направлении оси 0y равна F_y, то 2-й закон Ньютона для выделенного элемента имеет вид: dm a_y = F_y.

Выразим массу элемента через линейную (погонную) плотность r материала струны: dm = r dl = r dx.

На струну действует сила натяжения F. Эта сила при малых колебаниях практически постоянна по модулю по всей длине струны. Мы не будем учитывать незначительные изменения силы натяжения вследствие разной степени растяжения струны в разных ее точках. Итак, составляющая результирующей силы F_y в положительном направлении оси 0y равна:

Угол a мал, поэтому sina = tga = , поэтому можно записать

F_y = F — F = F .

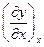
Индексы при производных указывают, в каких точках эти производные берутся. Разность в квадратных скобках есть приращение производной на длине dx: = = .

Итак, сила, действующая на элемент струны в направлении оси 0y, равна

F_y = F .

Второй закон Ньютона dm a_y = F_y для элемента струны примет вид:

r dx = F или = .

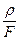
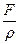
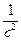
Отношение имеет размерность квадрата скорости. Обозначим эту скорость через c, тогда последнее уравнение примет вид:

= . (24)

Уравнение (24) и есть волновое уравнение, описывающее распространение бегущей волны в струне, где

c = (25)

есть фазовая скорость распространения волны (рис. 1-25).

Решение волнового уравнения. Решение дифференциального волнового уравнения называют уравнением волны. Решением волнового уравнения (24) является любая функция вида y = f(ct – x) или y = f(ct + x) [убедитесь в этом, подставив, например, функцию f(ct – x) в (24)]. Знак минус соответствует волне, бегущей в положительном направлении оси 0x, знак плюс – в отрицательном направлении. Если генератор, возбуждающий волну, совершает гармонические колебания, то в качестве решения следует, естественно, выбрать функцию синуса или косинуса. Выберем, например, функцию синуса, тогда уравнение бегущей волны примет вид:

y = а sin [ (ct – x) +j ]. (26)

Из произведения x следует смысл l. При x = l фаза волны сдвигается на 2p радиан, следовательно, длина волны l – это минимальное расстояние между двумя частицами струны, которые колеблются в фазе. Из соотношения = w = следует, что фазовая скорость равна c = . Фазовая скорость c определяет скорость распространения некоторой фазы волны (рис. 1-25).

Так как = kc = w, x = kx и с = , то уравнение бегущей волны (26) можно записать в виде

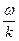
Обратим внимание на то обстоятельство, что в составляющих аргумента уравнения бегущей волны отражены как пространственный (kx), так и временной (wt) аргументы волнового процесса. Если фиксировать координату x, то уравнение волны описывает гармонические колебание элемента (частицы) струны в точке с этой координатой. Если фиксировать время t, то уравнение волны описывает пространственные смещения частиц струны по всей ее длине в этот момент времени (струна имеет форму синусоиды). Оба аргумента – пространственный (kx) и временной (wt) – совместно описывают бегущую волну в пространстве и времени. Циклическая частота w = определяет сдвиг фазы в волне за единицу времени, волновое число k = определяет сдвиг фазы при перемещении волны на единицу длины.

Запишем уравнение плоской упругой волны в среде при произвольном направлении относительно системы отсчета. Допустим, плоская акустическая волна распространяется в упругой среде в направлении единичного вектора n относительно выбранной декартовой системы координат (рис. 1-26). В качестве начальной волновой поверхности выберем поверхность, проходящую через начало координат (на рисунке – это поверхность А). Колебания некоторой характеристики акустического поля h на начальной поверхности определится уравнением h_А = а sin (wt + j ).Через время t волновая поверхность сместится на расстояние l. Колебания h в любой точке этой новой поверхности, 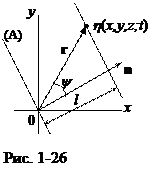определяемой радиус-вектором r, запишется в виде:

Скалярное произведение nr = r cos y = l, следовательно

Вектор k =knназывается волновым вектором, модуль которого равен волновому числу, и направленный перпендикулярно волновой поверхности. Таким образом, уравнение волны при произвольном направлении ее распространения запишется в виде:

Скалярноепроизведение kr = k_xx + k_yy + k_zz. Проекции волнового вектора можно представить через направляющие косинусы:

k_x = cosa, k_y = cosb, k_y = cosg,

1.2.2. Стоячие волны на струне

Стоячая волна формируется в результате интерференции многократно отраженных бегущих волн от точек закрепления струны.

Бегущая волна «1», перемещающаяся в положительном направлении оси 0x, описывается уравнением волны:

Отраженная бегущая волна «2», перемещающаяся в отрицательном направлении оси 0x, имеет вид:

Определим соотношение между начальными фазами j₁ и j₂. В точке закрепления струны «B» (x = 0) колебания струны отсутствует:

Это уравнение справедливо при выполнении двух условий:

Условие a₁ = a₂ означает, что отсутствуют потери энергии волны при отражении. Условие j₂= j ₁ + p указывает, что отраженная волна сдвинута по фазе от падающей волны на p радиан. Итак, уравнение бегущей волны «2» имеет вид: y₂ = a₂ sin (wt + kx + j ₁ + p).

Волна «2» отражается от опоры «B». Отраженная волна «3», которая перемещается в положительном направлении оси 0x, имеет вид:

Определим соотношение между начальными фазами j₁ и j_3. Вточке крепления струны «A» колебание струны отсутствует:

справедливо при выполнении двух условий:

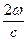
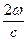
Волны «1» и «3» движутся в одну сторону. Результат сложения этих волн зависит от разности фаз между этими волнами. Итак, разность фаз волн «1» и «3» равна L. Если разность фаз равна целому числу полного угла 2p, т.е. если L = n2p (n = 1, 2, …), (28)

то волны «1» и «3» находятся в фазе, и их амплитуды складываются – наблюдается максимум интерференции этих волн. В противном случае волны будут гасить друг друга. Подставляя связь между круговой частотой и длиной волны w = в соотношение (28), получим:

L = n . (28 * )

Синфазное распространение волн «1» и «3» реализуется, если на длине струны укладывается целое число полуволн.

Если условие (28 * ) не выполняются, то при многократном отражении разность их фаз непрерывно изменяется, что приводит к уменьшению результирующей амплитуды, волны начинают гасить друг друга.

Уравнение стоячей волны. Результирующее колебание струны обусловлено интерференцией встречных волн. Обозначим результирующую амплитуду волн [при выполнении условия (28 * )], бегущих в положительном направлении оси 0x, через Y_(®), а в обратном направлении – через Y₍₎. Здесь: Y_(®) = a₁ + a₃ + a₅ + … ; Y₍₎= a₂ + a₄ + a₆ + … Вследствие потерь энергии результирующие амплитуды Y_(®)и Y₍₎ имеют конечное значение и не равны друг другу. Уравнение результирующей волны, бегущей в положительном направлении оси 0x, имеет вид:

Уравнение результирующей волны, бегущей в отрицательном направлении оси 0x, имеет вид:

Прибавим и вычтем вспомогательную величину[Y_(®)×sin (wt + kx)], получим:

Уравнение (29) описывает волновой процесс в струне.

Проведем анализ уравнения.

1. При Y_(®) = Y₍₎ в уравнении (29) остается первый член, который описывает стоячую волну: y =-2Y_(®)sin kx ×cos wt. Второй член в (29) равен нулю. Амплитуда колебаний частиц струны 2Y_(®)sinkx определяется координатой этих частиц. В точках с координатами, отвечающими условию sin kx = 0, т.е. условию kx = np, колебания отсутствуют. Эти точки на струне называются узлами стоячей волны. Координаты узлов: т.к. k = , то

x_узел = n , n = 1, 2, 3, …

L = n = n , то n_n = n , или n_n = n т.к. c = .

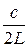
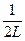
Определим максимумы интерференции встречных волн. В точках струны, отвечающих условию ÷sin kxê = 1, имеем максимумы амплитуды колебания в стоячей волне. Эти максимумы называются пучностями стоячей волны. Так как kx =(2n + 1) 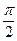, где n = 1, 2, …, то координаты пучностей определяются формулой x_пучн. = (2n + 1) .

График стоячей волны в отсутствии потерь приведен на рис. 1-28. Частицы струны между узлами колеблются в фазе. При переходе через узел фаза изменяется на p радиан (противофазные колебания частиц на соседних участках струны при переходе через узел).

В стоячей волне энергия не переносится, в узлах колебания отсутствуют. Однако в отсутствии потерь нет и необходимости компенсировать потери. В реальном же эксперименте потери неизбежны, поэтому Y_(®) ¹ Y₍₎, и бегущая волна вызывает небольшие колебания в узлах, вследствие чего узлы размываются.

1.2.3. Импеданс среды (на примере струны)

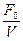
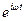
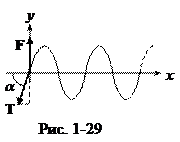
В § 1.1.7 выяснили, что феноменологический смысл механического импеданса колебательной системы определяется как внешняясила, которая необходима для сообщения колебательной системе единичную амплитудную скорость Z = . Определим импеданс струны как среды, в которой распространяется волна. Так как в струне распространяется поперечная волна, то этот импеданс естественно назвать поперечным импедансом. Подействуем на струну внешней гармонической силой F = F₀ в точке x = 0 в перпендикулярном направлении к струне. В этом случае уравнение бегущей волны имеет вид: y = a .

Пусть натяжение струны T. В вертикальном направлении имеем:

Следовательно, импеданс струны определяется выражением:

Z = = = .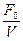

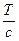
Фазовая скорость волны связанас натяжение T и плотностью струны r соотношением c = , поэтому можно записать:

Отметим, импеданс среды еще называют волновым сопротивлением среды.

1.2.4. Отражение и прохождение волны на границе двух сред

Источник