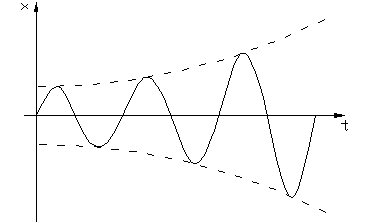
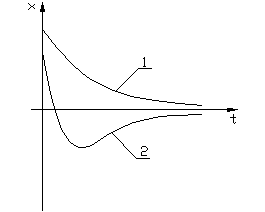
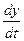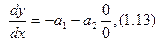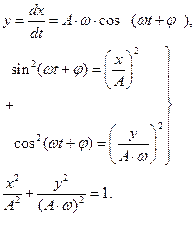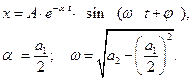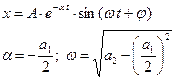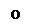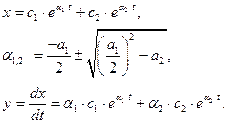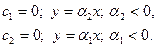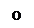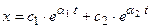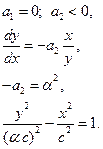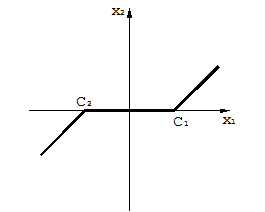Что такое фазовая плоскость

Фазовая плоскость

Фазовая плоскость — координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты), однозначно определяющие состояние системы второго порядка. [1] Фазовая плоскость является частным случаем фазового пространства, которое может иметь бо́льшую размерность.

В физике колебаний на оси абсцисс фазовой плоскости откладывается значения параметра x, а на оси ординат – первая производная x по времени (что, очевидно, связывает ось ординат с импульсом. См. Фазовое пространство). [2]

См. также

Источники

Полезное

Смотреть что такое «Фазовая плоскость» в других словарях:

фазовая плоскость — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN phase plane … Справочник технического переводчика

фазовая плоскость — fazinė plokštuma statusas T sritis automatika atitikmenys: angl. phase plane vok. Phasenebene, f rus. фазовая плоскость, f pranc. plan de phase, m … Automatikos terminų žodynas

фазовая плоскость — fazinė plokštuma statusas T sritis fizika atitikmenys: angl. phase plane vok. Phasenebene, f rus. фазовая плоскость, f pranc. plan des phases, m … Fizikos terminų žodynas

ФАЗОВАЯ ПЛОСКОСТЬ — плоскость R2, используемая для геометрич. интерпретации автономной системы двух обыкновенных дифференциальных уравнений 1 го порядка. Ф. п. частный случай фазового пространства. См. также Динамическая система (где эта интерпретация названа… … Математическая энциклопедия

Фазовая диаграмма — У этого термина существуют и другие значения, см. Фазовая плоскость. Фазовая диаграмма (диаграмма состояния) графическое отображение равновесного состояния бесконечной физико химической системы при условиях, отвечающих координатам рассматриваемой … Википедия

КОЛЕБАТЕЛЬНЫЕ РЕАКЦИИ — р ции, в ходе к рых концентрации промежут. соединений и скорость р ции испытывают колебания. Колебания м. б. периодическими, в этом случае значения c(t) колеблющихся концентраций (t время) можно представить рядом Фурье: где а n, bn коэффициенты… … Химическая энциклопедия

ФАЗОВОЕ ПРОСТРАНСТВО — совокупность всевозможных мгновенных состояний физич. (в широком смысле слова) системы, снабженная определенной структурой в зависимости от изучаемой системы и рассматриваемых вопросов. Ф. п. наз. также более конкретный объект пространство… … Математическая энциклопедия

Фазовое пространство — Двумерное фазовое пространство динамической системы (её развитие имеет вид расходящейся спирали) Фазовое пространство в математике и физике … Википедия

Phasenebene — fazinė plokštuma statusas T sritis automatika atitikmenys: angl. phase plane vok. Phasenebene, f rus. фазовая плоскость, f pranc. plan de phase, m … Automatikos terminų žodynas

fazinė plokštuma — statusas T sritis automatika atitikmenys: angl. phase plane vok. Phasenebene, f rus. фазовая плоскость, f pranc. plan de phase, m … Automatikos terminų žodynas

Источник

Фазовая плоскость

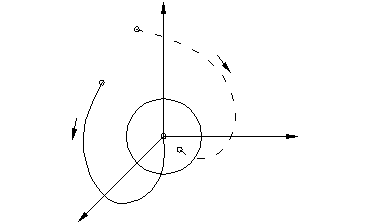
В физике колебаний на оси абсцисс фазовой плоскости откладывается значения параметра x, а на оси ординат — первая производная x по времени (что, очевидно, связывает ось ординат с импульсом. См. Фазовое пространство).Каждая точка фазовой плоскости отражает одно состояние системы и называется фазовой, изображающей или представляющей точкой. Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией. Через каждую точку фазовой плоскости проходит лишь одна фазовая траектория, за исключением особых точек. Стрелками на фазовых траекториях показывается перемещение изображающей точки с течением времени. Полная совокупность различных фазовых траекторий — это фазовый портрет. Он даёт представление о совокупности всех возможных состояний системы и типах возможных движений в ней. Фазовый портрет удобен для рассмотрения движений макроскопических и квантовых частиц.

Поскольку дифференцирование зашумленных функций относится к числу некорректно поставленных математических задач, то для практической реализации фазаграфии привлекаются специальные вычислительные процедуры фильтрации и регуляризации, обеспечившие надежную оценку производной наблюдаемого ЭКГ-сигнала.

Связанные понятия

В математике особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Особая точка векторного поля является положением равновесия или точкой покоя динамической системы, определяемой данным векторным полем: фазовая траектория с началом в особой точке состоит в точности из этой особой точки, а соответствующая ей интегральная кривая представляет собой прямую, параллельную оси времени.

В квантовой механике импульс, как и все другие наблюдаемые физические величины, определяется как оператор, который действует на волновую функцию.

Эта статья о физическом понятии. О более общем значении термина, см. статью СкалярСкалярная величина (от лат. scalaris — ступенчатый) в физике — величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д.Скалярная величина, или скаляр согласно математическому энциклопедическому словарю.

Статистическим ансамблем физической системы называется набор всевозможных состояний данной системы, отвечающих определённым критериям. Примерами статистического ансамбля являются.

О дискретном эквиваленте преобразования Лапласа см. Z-преобразование.В математике дискретный оператор Лапласа — аналог непрерывного оператора Лапласа, определяемого как отношения на графе или дискретной сетке. В случае конечномерного графа (имеющего конечное число вершин и рёбер) дискретный оператор Лапласа имеет более общее название: матрица Лапласа.

Источник

Фазовое пространство и фазовая плоскость

Этот метод применим для систем с уравнениями не более второго порядка.

Переходные процессы, вызванные какими-либо начальными отклонениями координат (при отсутствии внешних воздействий), описываются нелинейными дифференциальными уравнениями динамики в нормальной форме

(1.2.1)

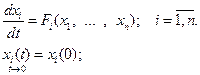
где x_i – координаты состояния системы, 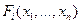— нелинейные функции.

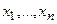
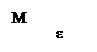Если координаты состояния x_i принять за координаты n-мерного пространства, то любой комбинации переменных соответствует определенное состояние или фаза системы, поэтому пространство называют фазовым.

x3,…, xn
x2
x1	Рис. 1.2.1

Точку М вn-мерном пространстве, характеризующую действительное (настоящее) состояние системы, называют изображающей. Изменению состояния системы соответствует движение точки 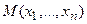по траектории, называемой фазовой. Совокупность фазовых траекторий называют фазовым портретом системы.

Для асимптотически устойчивых систем точка М движется по фазовым траекториям к началу координат.

В случае устойчивых систем точка М движется в область e вокруг начала координат.

По фазовым портретам системы можно судить об устойчивости движения.

Поскольку изображение n-мерного пространства практически невозможно, то наиболее широко распространен метод фазовой плоскости (n=2). Уравнения (1.2.1) при этом имеют вид:

; (1.2.2)

; (1.2.3)

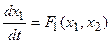
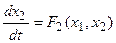
Дифференциальное уравнение фазовых траекторий получим, исключая время из уравнений (1.2.2 и 1.2.3), путём деления уравнения (1.2.3) на уравнение (1.2.2)

; (1.2.4)

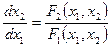
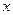
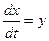
Большую информативность фазовых портретов даёт применение в качестве координат переменных и скорости её изменения , причём переменная у откладывается по оси ординат.

Система уравнений (1.2.4) при этом преобразуется к виду:

(1.2.5)

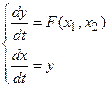
Фазовая плоскость с этой системой координат обладает следующими свойствами:

а) в верхней полуплоскости (рис.1.2.2) направление движения по траекториям слева направо, т.е. в сторону увеличения x, так как там скорость y>0, а в нижней полуплоскости, наоборот, – справа налево

б) ось x пересекается фазовыми траекториями под прямым углом, т.к. в точках пересечения скорость y=0, т.е. имеет место максимум или минимум величины x.

1.3. Типы особых точек и фазовые траектории линейных систем

Рассмотрим линейную систему, движение в которой описывается уравнением:

Решим уравнение (1.8) относительно старшей производной

Введем новую переменную

, =

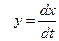
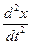
Разделим (1.10) на (1.11) и получим дифференциальное уравнение (ДУ) фазовых траекторий

В точках, соответствующих установившемуся состоянию ( x=0, y=0), получаем согласно уравнению (1.12) выражение

то есть неопределенное направление касательных к интегральным кривым. Эти точки называют особыми и они классифицируются, т.е. им присвоены названия.

Уравнению (1.8) соответствуют корни характеристического уравнения

(1.14)

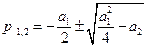
В зависимости от знаков и величины коэффициентов a₁ и а₂ возможны шесть случаев корней характеристического уравнения и соответствующих им фазовых траекторий.

Рассмотрим эти случаи подробнее:

1) a₁=0, a₂>0 – корни чисто мнимые.

Линейная система на границе устойчивости (в системе возникают незатухающие колебания).

2) a₁>0, a₂>0, дискриминант D 0, дискриминант D 0, a₂>0, дискриминант D>0 – корни вещественные, отрицательные.
Линейная система устойчива, процессы апериодические.

5) a₁ 0, дискриминант D>0 – корни вещественные, положительные.
Линейная система неустойчива, процессы апериодические.

6) a₁>0, a₂ 0 – корни вещественные, разных знаков. Линейная система неустойчива, процессы апериодические.

Рассмотрим фазовые траектории для каждого случая в отдельности.

1. Если рассматривать движение от оси абсцисс, то можно записать , , а величины А и определяются начальными условиями.

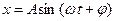
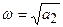
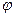
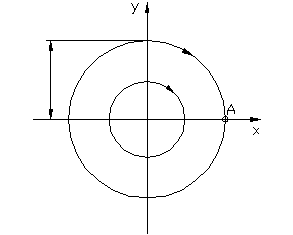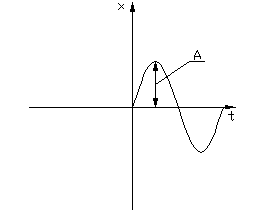
Незатухающим колебаниям в системе (рис.1.3.1а) соответствует движение изображающей точки М (рис.1.3.1б) по замкнутым траекториям эллиптического вида.

Точка О (x=0; y=0) – особая точка, центр.

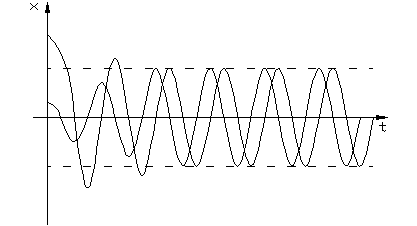
2. Корни комплексные с отрицательными вещественными частями

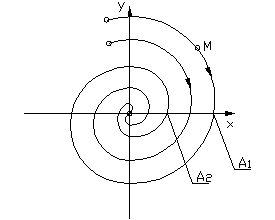
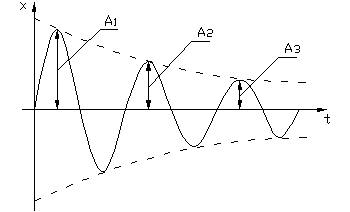
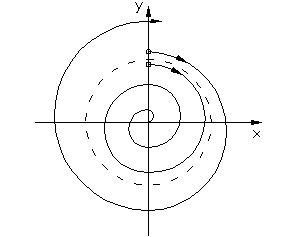
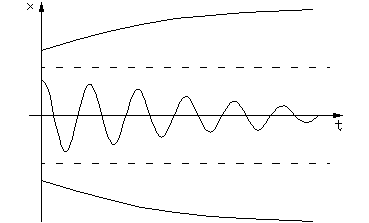
Затухающим колебаниям (рис.1.3.2а) в системе на фазовой плоскости (рис.1.3.2.б) соответствуют спиралевидные траектории, по которым изображающая точка стремится к началу координат. Точка О – особая точка – устойчивый фокус.

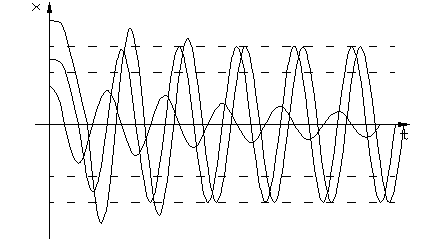
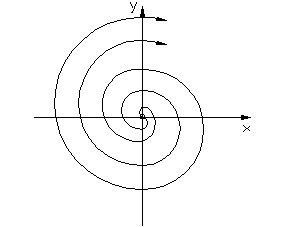
3. Корни комплексные с положительными вещественными частями.

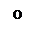Расходящимся колебаниям в системе на фазовой плоскости соответствуют спиралевидные траектории, по которым изображающая точка удаляется от начала координат. Особая точка О – неустойчивый фокус.

4. Корни вещественные, отрицательные.

Переходные процессы апериодические двух типов: монотонные (1) и с перерегулированием (2).

Монотонные процессы получаются при выполнении условий:

Соответствующие им фазовые траектории имеют вид прямых линий (рис.1.3.4б).

Особая точка О – устойчивый узел.

Фазовые траектории, имеющие точку равновесия в виде устойчивого узла, соответствуют апериодическому затухающему переходному процессу.

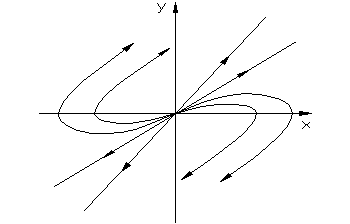
5. Корни вещественные, положительные.

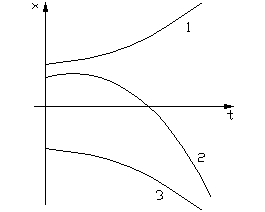
Выражения такие же, как в предыдущем случае, только α меняет знак

Движение изображающей точки направлено от точки равновесия системы к бесконечной удаленной точке фазовой плоскости. В этом случае положение равновесия системы неустойчивое.

Особая точка О – неустойчивый узел.

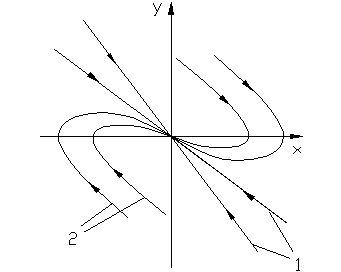
6. Корни вещественные разных знаков.

Процессы апериодические неустойчивые (рис.1.3.6а).

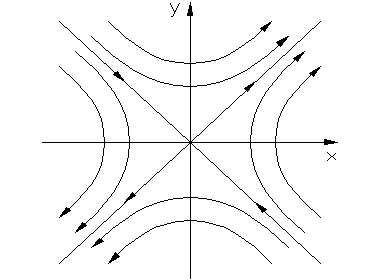
Где С- постоянная интегрирования.

Фазовые траектории имеют вид гипербол.

Особая точка О называется «седло».

Седло всегда неустойчиво.

1.4. Особые линии в нелинейных системах

Во многих случаях реальные САУ можно считать линейными лишь при малых отклонениях перемененных от их заданных значений в установившемся состоянии. При этом их фазовые портреты соответствуют особым точкам линейных систем. При больших отклонениях из-за наличия нелинейностей характер движений и фазовые портреты могут существенно отличаться от портретов линейных систем, при этом возможны следующие случаи:

1. Устойчивый граничный периодический режим с амплитудой колебаний а₁.

При малых начальных отклонениях система может оказаться неустойчивой. Поэтому согласно линейной теории колебания начинают расходиться, но из-за наличия нелинейности их амплитуда ограничивается предельной величиной а₁. При больших начальных отклонениях система становится устойчивой и колебания затухают, но не до нуля, а до а₁. Т.е. система генерирует колебания с постоянной амплитудой и частотой, которые называют автоколебаниями.

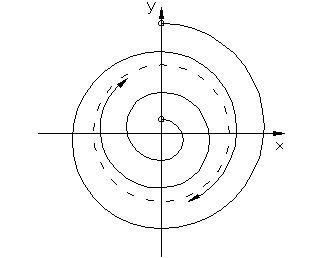
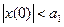
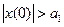
Картина фазовых траекторий, соответствующая такому случаю имеет вид (рис.1.4.1б).

Вблизи начала координат имеют место спирали как в неустойчивой линейной системе с особой точкой «неустойчивый фокус». Но далее они расходятся не до бесконечности, а приближаются асимптотически к некоторому замкнутому контуру ограниченных размеров.

К нему же приближаются спирали вне контура (устойчивый фокус). Т.е. на фазовом портрете нелинейной системы наблюдаются несколько особых точек линейных систем.

Устойчивым автоколебаниям на фазовой плоскости соответствует замкнутая траектория, к которой стремится изображающая точка, независимо от амплитуды начальных отклонений. Эта замкнутая траектория представляет первый тип особых линий и называется устойчивый предельный цикл. Размеры предельного цикла по осям координат представляют амплитуду колебаний а₁ и скорость её изменения. Для нахождения периода колебаний нужно решить дифференциальные уравнения системы.

2. Неустойчивый граничный периодический режим с амплитудой а₂. Равновесное состояние (х=0) системы устойчиво в « малом», т.е. и неустойчиво в «большом», т.е. . Здесь граничным процессом является неустойчивый периодический режим собственного движения системы с амплитудой а₂.

Рис. 1.4.2 б

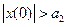
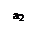Система устойчива в «малом» и неустойчива в «большом», неустойчивому периодическому режиму соответствует 2-ой тип особых линий – неустойчивый предельный цикл.

3. Если переходные процессы имеют вид (рис.1.4.3 а), то на фазовой плоскости им соответствуют два предельных цикла (ПЦ): неустойчивый ПЦ с амплитудой а₁ (рис.1.4.3б) и устойчивый ПЦ с амплитудой а₂.

а2

а1

Рис. 1.4.3 а

Рис. 1.4.3 б бю

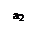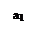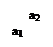В соответствии с рис.1.4.3 б система устойчива в «малом» и автоколебательна в «большом».

4. Апериодические процессы.

В случае апериодических процессов также возможны устойчивые и неустойчивые предельные циклы, при этом при различных амплитудах начальных отклонений процессы могут становиться либо колебательными, либо апериодическими.

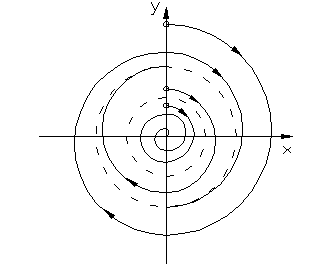
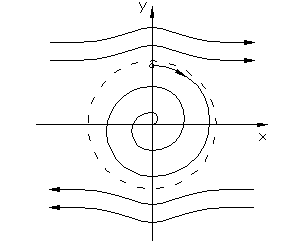
В нелинейной системе при больших отклонениях переменных колебательные процессы могут переходить в апериодические (рис. 1.4.4 а,). На фазовой плоскости наблюдается неустойчивый ПЦ (рис.1.4.4.б).

Система устойчивы в «малом» и неустойчива в «большом».

5. Система согласно линейной теории находится на границе устойчивости.

.

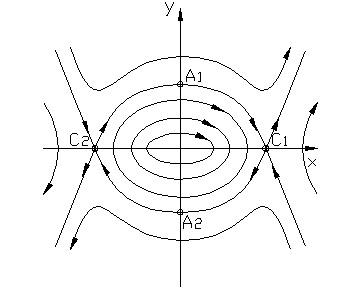
Линии и , разделяющие фазовые траектории разных типов называют сепаратрисами – третий вид особых линий.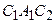

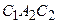
6. Для ряда нелинейных систем с зонами нечувствительности (рис.1.4.6.а), люфтом, сухим трением характерно отличие от рассмотренных случаев, состоящее в том, что в них приближение к линейной системе наступает, при достаточно больших отклонениях переменных, т.е. их можно рассматривать как линейные в «большом», а не в «малом».

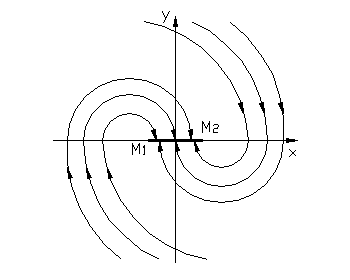
Наличие зоны нечувствительности проявляется в том, что установившемуся состоянию равновесия при данной нагрузке соответствует не одна точка на фазовой плоскости (рис.1.4.6.б), а отрезок состояний равновесия, т.е. изображающая точка попадает не в начало координат, а на отрезок покоя М₁М₂, при этом система не обладает асимптотической устойчивостью. Длина этого участка зависит от ширины зоны нечувствительности.

Глава 2. Фазовая плоскость систем, описываемых уравнениями с неаналитической правой частью

В дифференциальных уравнениях с неаналитической правой частью, последняя не раскладывается в ряды по степеням аргументов (х,у).

2.1. Исследование системы со скользящим режимом

Рассмотрим систему, которая содержит объект с самовыравниванием, безынерционный чувствительный элемент, усилитель мощности (золотник) и серводвигатель постоянной скорости.

В общем случае объект управления с самовыравниванием описывается уравнением:

— постоянная времени,

— коэффициент самовыравнивания,

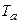
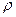
— если r>0 – объект статически устойчив, и задачей регулятора является обеспечение требуемого качества управления;

-если r S`(τ), то колебания затухающие, система устойчива.

Источник