что такое базовый случай рекурсивной функции
Рекурсия. Занимательные задачки
В этой статье речь пойдет о задачах на рекурсию и о том как их решать.
Кратко о рекурсии
Рекурсия достаточно распространённое явление, которое встречается не только в областях науки, но и в повседневной жизни. Например, эффект Дросте, треугольник Серпинского и т. д. Один из вариантов увидеть рекурсию – это навести Web-камеру на экран монитора компьютера, естественно, предварительно её включив. Таким образом, камера будет записывать изображение экрана компьютера, и выводить его же на этот экран, получится что-то вроде замкнутого цикла. В итоге мы будем наблюдать нечто похожее на тоннель.
В программировании рекурсия тесно связана с функциями, точнее именно благодаря функциям в программировании существует такое понятие как рекурсия или рекурсивная функция. Простыми словами, рекурсия – определение части функции (метода) через саму себя, то есть это функция, которая вызывает саму себя, непосредственно (в своём теле) или косвенно (через другую функцию).
Задачи
При изучении рекурсии наиболее эффективным для понимания рекурсии является решение задач.
Любой алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационном виде и наоборот. Останется вопрос, надо ли это, и насколько это будет это эффективно.
Для обоснования можно привести такие доводы.
Для начала можно вспомнить определение рекурсии и итерации. Рекурсия — это такой способ организации обработки данных, при котором программа вызывает сама себя непосредственно, либо с помощью других программ. Итерация — это способ организации обработки данных, при котором определенные действия повторяются многократно, не приводя при этом к рекурсивным вызовам программ.
После чего можно сделать вывод, что они взаимно заменимы, но не всегда с одинаковыми затратами по ресурсам и скорости. Для обоснования можно привести такой пример: имеется функция, в которой для организации некого алгоритма имеется цикл, выполняющий последовательность действий в зависимости от текущего значения счетчика (может от него и не зависеть). Раз имеется цикл, значит, в теле повторяется последовательность действий — итерации цикла. Можно вынести операции в отдельную подпрограмму и передавать ей значение счетчика, если таковое есть. По завершению выполнения подпрограммы мы проверяем условия выполнения цикла, и если оно верно, переходим к новому вызову подпрограммы, если ложно — завершаем выполнение. Т.к. все содержание цикла мы поместили в подпрограмму, значит, условие на выполнение цикла помещено также в подпрограмму, и получить его можно через возвращающее значение функции, параметры передающееся по ссылке или указателю в подпрограмму, а также глобальные переменные. Далее легко показать, что вызов данной подпрограммы из цикла легко переделать на вызов, или не вызов (возврата значения или просто завершения работы) подпрограммы из нее самой, руководствуясь какими-либо условиями (теми, что раньше были в условии цикла). Теперь, если посмотреть на нашу абстрактную программу, она примерно выглядит как передача значений подпрограмме и их использование, которые изменит подпрограмма по завершению, т.е. мы заменили итеративный цикл на рекурсивный вызов подпрограммы для решения данного алгоритма.
Задача по приведению рекурсии к итеративному подходу симметрична.
Подводя итог, можно выразить такие мысли: для каждого подхода существует свой класс задач, который определяется по конкретным требованиям к конкретной задаче.
Более подробно с этим можно познакомиться тут
Так же как и у перебора (цикла) у рекурсии должно быть условие остановки — Базовый случай (иначе также как и цикл рекурсия будет работать вечно — infinite). Это условие и является тем случаем к которому рекурсия идет (шаг рекурсии). При каждом шаге вызывается рекурсивная функция до тех пор пока при следующем вызове не сработает базовое условие и произойдет остановка рекурсии(а точнее возврат к последнему вызову функции). Всё решение сводится к решению базового случая. В случае, когда рекурсивная функция вызывается для решения сложной задачи (не базового случая) выполняется некоторое количество рекурсивных вызовов или шагов, с целью сведения задачи к более простой. И так до тех пор пока не получим базовое решение.
Тут Базовым условием является условие когда n=1. Так как мы знаем что 1!=1 и для вычисления 1! нам ни чего не нужно. Чтобы вычислить 2! мы можем использовать 1!, т.е. 2!=1!*2. Чтобы вычислить 3! нам нужно 2!*3… Чтобы вычислить n! нам нужно (n-1)!*n. Это и является шагом рекурсии. Иными словами, чтобы получить значение факториала от числа n, достаточно умножить на n значение факториала от предыдущего числа.
В сети при обьяснении рекурсии также даются задачи нахождения чисел Фибоначчи и Ханойская башня
Рассмотрим же теперь задачи с различным уровнем сложности.
Попробуйте их решить самостоятельно используя метод описанный выше. При решении попробуйте думать рекурсивно. Какой базовый случай в задаче? Какой Шаг рекурсии или рекурсивное условие?
Поехали! Решения задач предоставлены на языке Java.
A: От 1 до n
Дано натуральное число n. Выведите все числа от 1 до n.
Задачи по Python с решениями
Свежие записи
Рекурсия. Базовый случай и рекурсивный случай
На этом шаге рассмотрим понятие базового и рекурсивного случая.
Так как рекурсивная функция вызывает сама себя, программисту легко ошибиться и написать функцию так, что возникнет бесконечный цикл. Предположим, вы хотите написать функцию для вывода обратного отсчета:
Ее можно записать в рекурсивном виде:
Введите этот код и выполните его. И тут возникает проблема: эта функция
выполняется бесконечно!
Когда вы пишете рекурсивную функцию, в ней необходимо указать, в какой
момент следует прервать рекурсию. Вот почему каждая рекурсивная
функция состоит из двух частей: базового случая и рекурсивного случая.
В рекурсивном случае функция вызывает сама себя. В базовом случае
функция себя не вызывает (чтобы предотвратить зацикливание).
Добавим базовый случай в функцию countdown:
Теперь функция работает так, как было задумано. Это выглядит примерно
так:
Архив с примером на языке С++ можно взять здесь.
Архив с примером на языке Pascal можно взять здесь.
На следующем шаге продолжим рассматривать рекурсию.
Понимание рекурсии с помощью JavaScript
Russian (Pусский) translation by Ilya Nikov (you can also view the original English article)

Введение
Некоторые проблемы более естественным образом решаются с помощью рекурсии. Например, последовательность, подобная последовательности Фибоначчи, имеет рекурсивное определение. Каждое число в последовательности представляет собой сумму двух предыдущих чисел в последовательности. Проблемы, которые требуют, чтобы вы построили или пересекли древовидную структуру данных, также могут быть решены с помощью рекурсии. Обучение думать рекурсивно даст вам мощное умение решать такие проблемы.
В этом уроке я шаг за шагом приведу несколько рекурсивных функций, чтобы увидеть, как они работают, и показать методы, которые вы можете использовать для систематического определения рекурсивных функций.
Содержание:
Что такое рекурсия?
Вы берете линию один и говорите им «пожалуйста, держитесь». Затем вы берете линию два и ставите их на удержание. Затем вы поднимаете линию три и помещаете их в режим ожидания. Наконец, вы отвечаете на четвертую строку и говорите с вызывающим. Когда вы закончите с четвертым абонентом, вы повесите трубку и возьмете третий звонок. Когда вы закончите с третьим вызовом, вы повесите трубку и возьмете второй звонок. Когда вы закончите со вторым вызовом, вы повесите трубку и заберете первый звонок. Когда вы закончите этот звонок, вы можете, наконец, положить телефон.
Каждый из телефонных звонков в этом примере подобен рекурсивному вызову функции. Когда вы получаете звонок, он помещается в стек вызовов (в терминах кода). Если вы не можете выполнить звонок сразу, вы переводите вызов на удержание. Если у вас есть вызов функции, который не может быть сразу оценен, он остается в стеке вызовов. Когда вы можете ответить на звонок, он подбирается. Когда ваш код способен оценивать вызов функции, он выгружается из стека. Соблюдайте эту аналогию, просматривая приведенные ниже примеры кода.
Рекурсия с цифрами
Предположим, что у вас есть функция, которая будет суммировать числа от 1 до n. Например, если n = 4, сумма будет равна 1 + 2 + 3 + 4.
Сначала мы определяем базовый случай. Обнаружение базового случая можно также рассматривать как поиск случая, когда проблема может быть решена без рекурсии. В этом случае, когда n равно нулю. 0 не имеет частей, поэтому наша рекурсия может остановиться, когда мы достигнем 0.
Это то, что происходит на каждом шагу:
Это еще один способ увидеть, как функция обрабатывает каждый вызов:
Аргумент должен измениться в рекурсивном случае и приблизит вас к основному случаю. Этот аргумент должен быть протестирован в базовом случае. В предыдущем примере, поскольку мы вычитаем один из рекурсивного случая, мы проверяем, равен ли аргумент нулю в нашем базовом случае.
Задача
Рекурсия со списками
Повторение в списке похоже на повторение по числу, за исключением того, что вместо сокращения числа на каждом шаге мы уменьшаем список на каждом шаге, пока не дойдем до пустого списка.
Рассмотрим функцию sum, которая принимает список как входные данные и возвращает сумму всех элементов в списке. Это реализация для суммы функции:
Когда вы повторяетесь в списке, проверьте, не пуст ли он. В противном случае сделайте рекурсивный шаг в сокращенной версии списка.
Задача
Построение списков
Здесь функция eq возвращает true, если оба входа одинаковы. Функция cons использует элемент и список как входные данные и возвращает новый список с добавленным элементом к началу.
Мы будем проверять, совпадает ли первый элемент в списке с элементом, который мы хотим удалить. Если это так, удалите первый элемент из списка и верните новый список. Если первый элемент не равен элементу, который мы хотим удалить, мы берем первый элемент в списке и добавляем его на рекурсивный шаг. Рекурсивный шаг будет содержать список с удаленным первым элементом.
В ситуации, когда нам нужно создать список, мы берем первый элемент и добавляем его в рекурсивную часть нашего списка.
Задача
Обзор
Рекурсия похожа на итерацию. Любая функция, которую вы можете определить рекурсивно, также может быть определена с помощью циклов. Другие вещи, которые следует учитывать при использовании рекурсии, повторяются во вложенных списках и оптимизируют рекурсивные вызовы.
Отличным ресурсом для продолжения изучения рекурсии является книга The Little Schemer. Она учит вас мыслить рекурсивно, используя формат вопросов и ответов.
Рекурсия для неискушённых
Рекурсия для неискушённых
Вместо предисловия
Сейчас настало такое время, что в программирование, и в разработку интерфейсов в частности, стали приходить люди, не имеющие академического образования в области разработки ПО. Для малого и среднего бизнеса это, наверное, хорошо. Не нужно раскошеливаться на программистов, уже имеющих минимум 4 года работы за плечами. Но вот суровый энтерпрайз в этом отношении менее лоялен. Компиляция, интерпретация, AST, полиморфизм, SOLID, фасад, рекурсия — близкие выпускнику-программисту понятия, и в суровом энтерпрайзе он чувствует себя как минимум не одиноким.
Иная же ситуация с нами, реакт-программистами (да-да, и я тоже). Наступает момент, когда разработка интерфейсов требует не только вёрстки и создания «тупых» компонентов, но и знания фундаментальных инструментов программирования. И, к сожалению, такие метаморфозы часто не под силу стремящемуся из реакт-программистов в классические программисты. Литература, которая есть по фундаментальным основам программирования, безэмоциональна и беспощадна к новичкам. Для студентов-программистов ситуация иная, т.к. они варятся в этом «соку» несколько лет, и очередной бестселлер от дяди Боба или SICP не покажется им чем-то инопланетным.
Я попытаюсь без лишнего официоза, и при этом уделяя время деталям, познакомить всех причастных к проблеме «реакт-программистов» с одной из самых фундаментальных концепций программирования — рекурсией.
О значимости
Если суровый энтерпрайз — значит работа с данными. Если данные — то, скорее всего, в виде деревьев. Для работы с деревьями компьютерный бог не придумал ещё ничего лучше рекурсии. Но для начала нам нужно узнать врага в лицо, понять, как он работает изнутри. Ниже об этом.
Иди, вон, на кошках матрёшках тренируйся
Не переживайте — числа Фибоначчи, факториалы и прочие бояны — все будут рассмотрены. Матрёшка, а точнее процесс её изготовления идеально подходит для визуализации концепции рекурсии и процессов, происходящих внури неё. Напоминаю, что главной характеристикой матрёшки является количество матрёшек внутри — то есть вложенность, глубина матрёшки. Обозначим эту величину как n.
Как только работа закончена, матрёшку возвращают к предыдущему подмастерью, затем к предыдущему предыдущего и так до тех пор, пока не будут собраны все матрёшки.

Вот как может выглядеть этот процесс уже на JS:
Важно первым же делом проверить, а не базовый ли это случай? Не последняя ли матрёшка? Иначе рискуем рухнуть на питомник. Базовый случай всегда проверяется первым. Если нет, то строгаем матрёшки дальше.
Да, как можно заметить, подвызов всегда проще вызова. Т.е наш алгоритм идёт к уменьшению сложности до тех пор, пока вычисление уже не потребуется, т.к. уже нечего вычислять.
Декларативность
Нужно сказать пару слов о том, какая польза от рекурсии, если уже есть циклы. Уильям из Оккама недоволен.
В математике есть специальное обозначение для суммы нескольких чисел — Σ (сигма).
«Верни новый массив» — map()
«Преврати массив в Мегазорда» — reduce()
Напомню, что каждый из этих методов корнями уходит в ФП, где в основе всего лежит рекурсия. Всё иммутабельно, читабельно. Да и вообще стоит сказать, что есть языки программирования (Haskell вот), где вообще нет не только переменных, но и циклов. Только рекурсия, только хардкор!
— А что хочешь, то и пиши.
Как удачно выхваченная из контекста «Дневного дозора» фраза описывает рекурсию! «Что хочешь [получить], то и пиши». Рекурсия гораздо более юзерфрендли. Нам проще думать и рассуждать концепциями рекурсии. Декларативность рекурсии — важный, если не важнейший её плюс. Когда-нибудь нейросети смогут не только подражать Летову, но и писать код в суровом энтерпрайзе. Но пока с кодом работают люди, приоритетнее будет его читабельность и поддержка, а не скорость исполнения.
Ещё пара примеров, и двинемся дальше. Например, мы хотим найти сумму чисел в массиве:
Классика декларативного жанра: мы не пишем подробно, что именно нужно сделать с каждым элементом. Мы хотим результат в зависимости от условий. Что хочу получить, то и пишу.
Ну и высший уровень — это использовние более сильных абстракций над рекурсией:
Одна строка, ничего лишнего.
И ещё раз о деревьях, но уже подробнее. Собственно говоря, для деревьев пока не придумали ничего лучше рекурсии. Из полезного инструмента рекурсия превращается в жемчужину, когда мы имеем дело с деревьями.
Стандартный боян: нужно реализовать функцию, принимающую дерево и возвращающую массив листьев.
Мы хотим получить что-то такое:
И это ещё детский сад. На уровнях три и более начинается самый настоящий шабаш макарон и черных техник. И это мы только пытаемся получить массив листьев, ни о каких манипуляциях с полученным массивом не идёт и речи.
То же самое, но уже рекурсивно:
Вот и всё, и это решение работает для любых уровней вложенности.
Ещё раз обращу внимание: рекурсия — это не панацея и не серебрянная пуля от всех проблем. Существуют проблемы, которые гораздо проще решаются циклами. Более того, чаще всего рекурсивное решение менее производительно (об этом далее).
Без лишних слов, самый большой недостаток рекурсии: Uncaught RangeError: Maximum call stack size exceeded
Вот сейчас самое время заглянуть под капот и понять, почему же это происходит. Тут нам вновь стоит обратиться в столярную мастерскую.
Случаются заказы, когда, например, не было указано базовое условие или нам нужна матрёшка планковской длины, и тогда подмастерий набивается в мастерскую так много, что стены и перекрытия не выдерживают и мастерская падает на кошачий питомник.
К сожалению, в реальном мире ещё не придумали способ предотвратить такую кОтастрофу, кроме как уволить всех подмастерий и не делать матрёшек вообще. Во фронтенде немного иначе: RangeError — это защита JS-движка от падения нашей программы. Как только движок видит, что стек начинает странно расти, выполнение программы прерывается. Движок выбрасывает эту ошибку, предотвращая переполнение памяти.
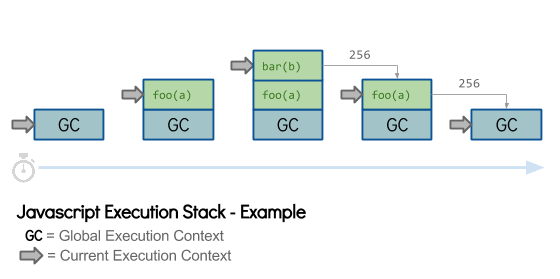
Разбираться в этом нужно с понимания того, что такое стек вызова. Это среда, в которой выполняются функции. Каждый вызов функции влечёт за собой выделение фрагмента (фрейма) памяти. Фрейм содержит определённую информацию о текущем состоянии выполнения функции, включая значения любых переменных. Причина, по которой эта информация должна храниться во фрейме, состоит в том, что функция может вызывать другую функцию, которая приостанавливает текущую функцию. Когда другая функция заканчивается, движку необходимо восстановить точное состояние с момента его приостановки.
Давайте визуализируем этот процесс в общем (без циклов/рекурсий) случае.
Диаграммы такого вида украдены мною отсюда.
Когда функция закачивает свою работу, её фрейм удаляется, выпадает из стека.
Вот, кажется, вся теория по стеку, которая нам нужна. Теперь посмотрим, как ведет себя стек при работе с циклами и рекурсиями.
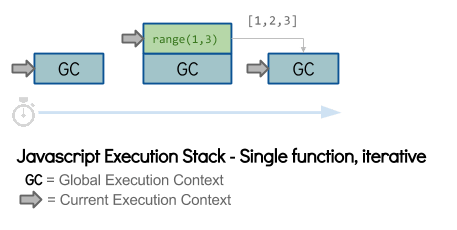
Есть функция, возвращающая нам массив чисел, находящийся между заданными точками:
Ничего удивительного, алгоритм работает просто и эффективно расходует память (создался только один фрейм).
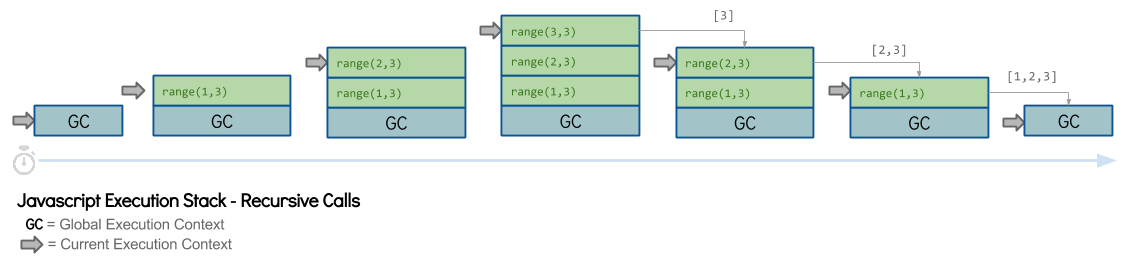
Иная ситуация будет, если мы перепишем функцию в рекурсивный вид:
Стек начинает расти. Ну и что? Чтобы это стало проблемой, мы должны получить тысячи вызовов в контексте. В современных реалиях такая ситуация практически невозможна. Но только не в случае с рекурсией.
В общем-то ещё не произошло ничего страшного, но движок, анализируя лавинообразный рост стека понимает, что что-то пошло не так, и останавливает выполнение программы.
Пора озвучить главный недостаток рекурсии: расход памяти. Далее будут описаны способы избежать роста стека и гибели кошек заодно.
Хвостовые вызовы
Надо сказать, что сама идея хвостовых вызовов не нова и напрямую не связана ни с рекурсией, ни с JS. Еще в 1960-х годах, когда компьютеры были великанами, было сделано важное наблюдение — если любой вызов является последней операцией перед возвратом из функции, то стек нам не нужен. Если рекурсивный вызов является последней операцией перед выходом из вызывающей функции, и результатом вызывающей функции должен стать результат, который вернёт рекурсивный вызов, то сохранение контекста уже не имеет значения — ни параметры, ни локальные переменные использоваться уже не будут, а адрес возврата уже находится в стеке. Ещё раз: если вызов bar из baz происходит в самом конце выполнения baz (иначе говоря «в хвосте»), то стек вызовов для baz не нужен вовсе.
Хвостовой вызов выглядит так, и никак иначе (чистый хвостовой вызов aka Proper Tail Call aka PTC):
… не хвостовые вызовы.
Приведение кода к хвостовому вызову называется оптимизацией хвостового вызова (далее по тексту TCO — Tail Call Optimization). TCO по умолчанию есть во многих языках, активно использующих рекурсию — например в Haskell. Там компилятор, видя вызов в «хвосте» (tail call position), применяет оптимизацию, приводя рекурсию к циклу.
Непременно нужно отметить, что TCO-версия получена с помощью Babel и лишь отчасти отражает действительный результат оптимизации компилятором. Но суть передана на 100% верно: рекурсия будет превращена в цикл. Реальный результат в виде ассемблерного кода слишком низкоуровневый, чтобы человек смог его осилить.
Получается, что ТCO в случае рекурсии решает главную проблему — потребление памяти. Это не значит, что программа будет работать быстрее, зачастую хвостовые вызовы работают медленее обычных. И в этом плане TCO не является оптимизацией в её привычном понимании — оптимизацией скорости работы. Но TCO позволяет нам использовать рекурсию там, где это необходимо, не беспокоясь о переполнении стека. А это важнее скорости, ибо, как уже писалось, рекурсия гораздо более декларативна: Что хочу получить, то и пишу.
Ну и конечно же, в мире фронтенда TCO не было до ES6) Вспоминается старик Крокфорд:
Any sufficiently interesting JavaScript library contains an ad hoc, informally-specified, bug-ridden, slow implementation of half of Haskell.
«Любая достаточно интересная библиотека JavaScript содержит забагованную, плохо документированную, медленную реализацию половины Haskell».
Тут, в общем-то, впору заканчивать статью: используйте Elm во фронтенде и не парьтесь насчет TCO, иммутабельности и типизации — всё идёт из коробки.
… продолжение для тех, кому Elm почему-то не подошёл
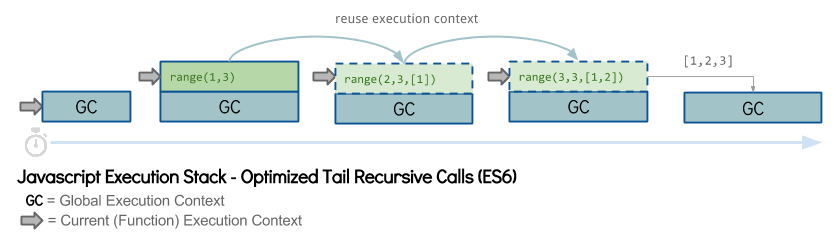
С приходом ES6 появилась возможность TCO и для JavaScript:
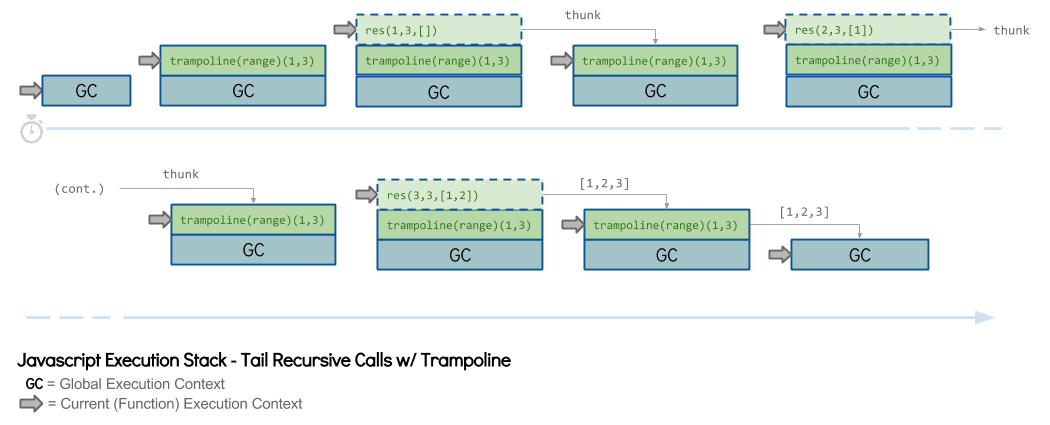
И посмотрим, как же теперь будет выглядеть использование стека:
Пунктир — это TCO. Как видно из диаграммы, нам теперь не нужны все фреймы вызовов, важен только последний, хвостовой. Происходит переиспользование текущего контекста для доступа к переменным прошлых вызовов. Стек больше не растёт.
Однако что-то пошло не так, и поддержка TCO была выпилена из 8-ой ноды. Спорное решение, и судьба TCO в дальнейшем неизвестна(
Если хотите эффективно использовать рекурсию у себя в проектах — либо оставайтесь на шестой ноде, либо используйте …
…трамплины
Суть метода заключается в создании утилиты (трамплина), представляющей собой функцию высшего порядка. Основа работы этой функции — ленивые вычисления: вычисления откладываются до того момента, пока не понадобится их результат.
Идет проверка того, что нам возвращается — функция (рекурсивные вызовы) или результат (последняя матрёшка)? Как только нам возвращается не функция, цикл прекращает работу, трамплин срабатывает и возвращает искомое значение.
У этого подхода есть ряд преимуществ…
Т.е. необходимо переписать функцию в такой вид:
И посмотрим на диаграмму его выполнения:
К слову, вот ещё более каноничный, в реалиях ES6, вариант трамплина:
Заключение
Выводов сделано достаточно по ходу статьи, но один из них стоит подчеркнуть ещё раз.
Рекурсия — это не серебряная пуля и не панацея. На всякий случай напоминаю, что читаемость кода является нашей главной целью. Если рекурсия, наряду с описанными здесь стратегиями, приводит к тому, что код становится сложнее для понимания, то не используйте рекурсию; найдите другое решение.
Рекурсия в Python
Рекурсия — одна из фундаментальных концепций информатики, она важна как для программистов, так и для специалистов по обработке данных. Мало того, что многие алгоритмы сортировки и поиска рекурсивны, но каждое собеседование по Python будет включать некоторые вопросы, основанные на рекурсии. Это отмечает, что рекурсия является ключевой концепцией, которую необходимо пересмотреть перед любым собеседованием по кодированию.
Сегодня мы поможем вам освежить свои навыки рекурсивного программирования на Python и рассмотрим 6 практических задач, чтобы получить практический опыт.
Что такое рекурсия?
Рекурсия — это концепция в информатике, когда функция вызывает саму себя и выполняет цикл до тех пор, пока не достигнет желаемого конечного условия. Он основан на математической концепции рекурсивных определений, которая определяет элементы в наборе с точки зрения других элементов в наборе.
Каждая рекурсивная реализация имеет базовый случай, когда желаемое состояние было достигнуто, и рекурсивный случай, когда желаемое состояние не было достигнуто, и функция переходит на другой рекурсивный шаг.
Поведение в рекурсивном случае перед вызовом рекурсивной функции, внутренний самовызов, повторяется на каждом шаге. Поэтому рекурсивные структуры полезны, когда вы можете решить более серьёзную проблему (базовый случай), выполнив повторяющиеся подзадачи (рекурсивный случай), которые постепенно перемещают программу к базовому случаю.
Это приводит к поведению, аналогичному циклам for или while, за исключением того, что рекурсия приближается к целевому условию, в то время как for циклы выполняются заданное количество раз, а while циклы выполняются до тех пор, пока условие больше не будет выполняться.
Другими словами, рекурсия декларативна, потому что вы устанавливаете состояние, которого хотите достичь, а for/ while циклы являются итеративными, потому что вам нужно установить количество повторений.
Рекурсивные решения лучше всего подходят, когда проблема имеет чёткие подзадачи, которые необходимо повторить, и если вы не уверены, сколько раз вам нужно будет выполнить цикл с итеративным решением.
Например, если вы хотите создать программу-функцию факториала, которая находит факториал неизвестного числа.
Прямая против косвенной рекурсии
До сих пор мы обсуждали только прямую рекурсию, когда рекурсивная функция явно вызывает себя на своём рекурсивном шаге. Существует также косвенная рекурсия, когда рекурсивный вызов удаляется из функции, но всё ещё выполняется в результате исходного рекурсивного шага.
Например, functionAзвонки functionB, которые потом звонят function Aснова.
Плюсы и минусы рекурсии в Python
Все языки программирования поддерживают рекурсию, однако не все одинаково оптимизированы.
Итерация часто является предпочтительной в Python и считается более «питонической» из-за встроенных оптимизаций. Как правило, рекурсивные решения предпочтительнее итеративных решений при больших вычислениях, поскольку рекурсия часто приводит к меньшему количеству кода и более высокой производительности при масштабировании.
Плюсы
Минусы
Я не добавил удобочитаемости ни в один из столбцов, поскольку некоторые разработчики считают рекурсию более понятной, в то время как другие находят вложенное поведение запутанным. В конечном счёте, это индивидуально для каждой проблемы и разработчика.
Рекурсия в Python
Теперь давайте более подробно рассмотрим рекурсивные функции в Python.
Ниже приведён пример программы, которая рекурсивно печатает шаблон: 10 5 0 5 10.