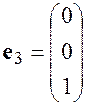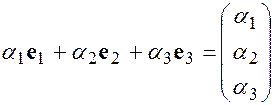что такое базисная строка и столбец

Что такое базисная строка и столбец

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Теорема о базисном миноре матрицы Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

§ 3. Теорема о базисном миноре матрицы

Указанные n равенств (1.42) удобно записать в виде одного равенства

Всякий раз, когда будет встречаться равенство (1.43), мы будем понимать его в смысле n равенств (1.42).
Введем теперь понятие линейной зависимости строк.
Определение. Строки A=(a₁,a₂. a_n), В = (b₁, b₂. b_n). С = (с₁, с₂. с_n) назовем линейно зависимыми, если найдутся такие числа α, β. γ не все равные нулю, что справедливы равенства

Указанные n равенств (1.44) удобно записать в виде одного равенства

а это и означает, что строка А является линейной комбинацией строк В. С.
2) Достаточность. Пусть одна из строк (например, А) является линейной комбинацией остальных строк. Тогда найдутся числа

Минором k-го порядка матрицы А будем называть определитель k- г о порядка с элементами, лежащими на пересечении любых k строк и любых k столбцов матрицы А. (Конечно, k не превосходит наименьшее из чисел т и п.)
Предположим, что хотя бы один из элементов а_ij матрицы А отличен от нуля. Тогда найдется такое целое положительное число r, что будут выполнены следующие два условия: 1) у матрицы А имеется минор r-го порядка, отличный от нуля, 2) всякий минор

(г + 1)-го и более высокого порядка (если таковые существуют) равен нулю.
Число г, удовлетворяющее требованиям 1) и 2), назовем рангом матрицы А ( р анг матрицы А, все элементы которой — нули, по определению равен нулю). Тот минор r-го порядка, который отличен от нуля, назовем базисным минором (конечно, у матрицы А может быть несколько миноров r-го порядка, отличных от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, назовем соответственно базисными строками и базисными столбцами.
Докажем следующую основную теорему.
Теорема 1.6 (теорема о базисном миноре). Базисные строки (базисные столбцы) линейно независимы. Любая строка (любой столбец) матрицы А является линейной комбинацией базисных строк (базисных столбцов).
Доказательство. Все рассуждения проведем для строк.
Если бы базисные строки были линейно зависимы, то по теореме 1.5 одна из этих строк являлась бы линейной комбинацией других базисных строк, и мы могли бы, не изменяя величины базисного минора, вычесть из этой строки указанную линейную комбинацию и получить строку, целиком состоящую из нулей, а это противоречило бы тому, что базисный минор отличен от нуля. Итак, базисные строки линейно независимы.
Докажем теперь, что любая строка матрицы А является линейной комбинацией базисных строк. Так как при произвольных переменах строк (или столбцов) определитель сохраняет свойство равенства нулю, то мы, не ограничивая общности, можем считать, что базисный минор находится в левом верхнем углу матрицы (1.47), т.е. расположен на первых г строках и первых г столбцах. Пусть j — любое число от 1 до n, а k — любое число от 1 до m.
Убедимся в том, что определитель (г + 1)-го порядка

(для всех j = 1, 2. n). Учитывая, что в последних равенствах алгебраическое дополнение c_r+1 = A_kj совпадает с заведомо отличным от нуля базисным минором, мы можем поделить каждое из этих равенств на c_r+1. Но тогда, вводя обозначения

Источник

Линейные комбинации строк и столбцов. Базисные строки и столбцы. Линейная независимость. Ранг матрицы. Вычисление ранга

Лекция 12

Свойство 6. Определитель треугольной матрицы равен произведению диагональных элементов.

=.

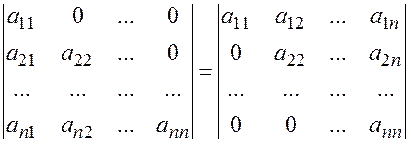
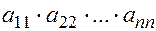
нижний треугольный верхний треугольный

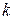
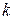
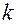
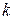
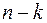
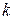
Определение. Минором -ого порядка матрицы называется детерминант матрицы порядка , образованный элементами, стоящими на пересечении выбранных строк и столбцов. Каждая матрица имеет столько миноров данного порядка, сколькими способами можно выбрать номера строк и столбцов. Если матрица квадратная, то каждому минору – огопорядка сопоставляется дополнительный минор, который по определению есть определитель матрицы порядка (), составленный из элементов, оставшихся после вычеркивания строк и столбцов.

Цель: изучить понятие линейной комбинации и линейной независимости строк и столбцов матрицы, методы вычисления ранга и определения базисного минора.

В теме «матрицы и действия над ними» мы ввели понятия матрицы строки и матрицы столбца,

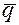
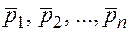
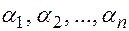
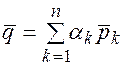
Определение. Столбец назовем линейной комбинацией столбцов одинаковой высоты, если при некоторых числах имеет место равенство:

(12.1)

Или в развернутом виде:

.

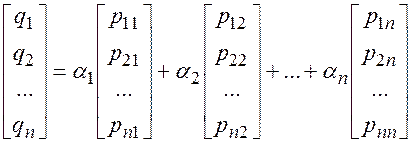
В силу определения умножения матриц на число и операции сложения последнее равенство можно представить в виде системы равенств, составленных для каждого элемента:

;

;

.

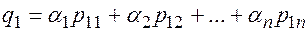
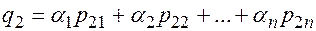
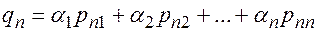
По аналогии с линейной комбинацией введем понятие линейной независимости строк и столбцов матрицы. Пусть 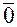— столбец у которого все элементы равны нулю.

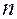
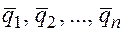
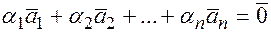
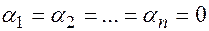
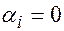
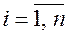
Определение. Система из столбцов называется линейно независимой, если из равенства следует, . В противном случае, если не все (), система столбцов линейно зависима.

Все утверждения записанные для столбцов, справедливы и для строк матрицы.

, ,

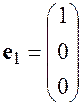
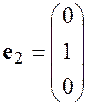
линейно независимы, т.к. их линейная комбинация

равна нулевому столбцу, только в случае, когда 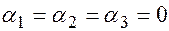, т.е. является тривиальной.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показать\скрыть

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Если система является неопределённой, указать базисное решение.

Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.

Источник

Линейная зависимость и независимость строк (столбцов) матрицы

Столбец называется линейной комбинацией столбцов одинаковых размеров, если

Если столбцы в (3.1) имеют вид

то матричному равенству (3.1) соответствуют поэлементные равенства

Аналогично формулируется определение линейной комбинации строк одинаковых размеров.

Здесь и далее символом о обозначается нулевой столбец соответствующих размеров.

1. Один столбец тоже образует систему: при — линейно зависимую, а при линейно независимую.

Пример 3.1. Используя определение, установить линейную зависимость или линейную независимость систем столбцов

2) Столбцы линейно независимы, так как равенство

Свойства линейно зависимых и линейно независимых столбцов матриц

Понятия линейной зависимости и линейной независимости определяются для строк и столбцов одинаково. Поэтому свойства, связанные с этими понятиями, сформулированные для столбцов, разумеется, справедливы и для строк.

1. Если в систему столбцов входит нулевой столбец, то она линейно зависима.

2. Если в системе столбцов имеется два равных столбца, то она линейно зависима.

4. Система из 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAiXFYMbEhAcBBoPDQoeAQ0I3cqgAAALZJREFUKM+VktsSwyAIRDWKiFf+/2uLSZvEhkxaXnTGs7KsGvN3UYrwC+ffa3D8zCMlxo+QlyfcNmg7v7A/t7VBux/jzkOe54lJURw8ZrHvop0UdM8P+3axGc89aqQ7XuxbjzybMkEUqPLAIPP6/u0g1OYUHnMpTQs02KLxq/0p0Y1O0al+RvqOCcv51CeZF1UeJBjhacoT6PJehTd9k/R7gdgPul7ei3itcWeYPp/sqv4fRhnzAuOaBpbDogV3AAAAAElFTkSuQmCC» /> столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.

5. Любые столбцы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система столбцов, содержащая линейно зависимую подсистему, линейно зависима.

Докажем, например, последнее свойство. Так как система столбцов линейно зависима, то существуют числа не все равные 0, что

Пример 3.3. Рассмотреть всевозможные системы, образованные из столбцов

Исследовать каждую систему на линейную зависимость.

Рассмотрим системы, содержащие по два столбца:

– каждая из четырех систем и линейно зависима, так как содержит нулевой столбец (свойство 1);

– система линейно зависима, так как столбцы пропорциональны (свойство 3): ;

– каждая из пяти систем и линейно независима, так как столбцы непропорциональные (см. утверждение примера 3.2).

Рассмотрим системы, содержащие три столбца:

– каждая из шести систем и линейно зависима, так как содержит нулевой столбец (свойство 1);

– системы линейно зависимы, так как содержат линейно зависимую подсистему (свойство 6);

– системы и линейно зависимы, так как последний столбец линейно выражается через остальные (свойство 4): и соответственно.

Наконец, системы из четырех или из пяти столбцов линейно зависимы (по свойству 6).

Источник

Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.

В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме «Матрицы. Виды матриц. Основные термины». Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.

Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:

Например, рассмотрим такую матрицу:

Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:

Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.

Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.

Для примера рассмотрим такую матрицу:

Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.

Введём ещё одно понятие – окаймляющий минор.

Для примера обратимся к такой матрице:

Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:

Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.

Для примера рассмотрим квадратную матрицу пятого порядка:

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник