что такое амплитудный спектр функции
Спектральный анализ сигналов
Не так давно товарищ Makeman описывал, как с помощью спектрального анализа можно разложить некоторый звуковой сигнал на слагающие его ноты. Давайте немного абстрагируемся от звука и положим, что у нас есть некоторый оцифрованный сигнал, спектральный состав которого мы хотим определить, и достаточно точно.
Под катом краткий обзор метода выделения гармоник из произвольного сигнала с помощью цифрового гетеродинирования, и немного особой, Фурье-магии.
Итак, что имеем.
Файл с отсчетами оцифрованного сигнала. Известно, что сигнал представляет собой сумму синусоид со своими частотами, амплитудами и начальными фазами, и, возможно, белый шум.
Будем решать данную задачу на Java.
Матчасть
Как я уже говорил, структура сигнала заведомо известна: это сумма синусоид и какая-то шумовая составляющая. Так сложилось, что для анализа периодических сигналов в инженерной практике широко используют мощный математический аппарат, именуемый в общем «Фурье-анализ». Давайте кратенько разберём, что же это за зверь такой.
Немного особой, Фурье-магии
Не так давно, в 19 веке, французский математик Жан Батист Жозеф Фурье показал, что любую функцию, удовлетворяющую некоторым условиям (непрерывность во времени, периодичность, удовлетворение условиям Дирихле) можно разложить в ряд, который в дальнейшем получил его имя — ряд Фурье.
В инженерной практике разложение периодических функций в ряд Фурье широко используется, например, в задачах теории цепей: несинусоидальное входное воздействие раскладывают на сумму синусоидальных и рассчитывают необходимые параметры цепей, например, по методу наложения.
Существует несколько возможных вариантов записи коэффициентов ряда Фурье, нам же лишь необходимо знать суть.
Разложение в ряд Фурье позволяет разложить непрерывную функцию в сумму других непрерывных функций. И в общем случае, ряд будет иметь бесконечное количество членов.
Дальнейшим усовершенствованием подхода Фурье является интегральное преобразование его же имени. Преобразование Фурье.
В отличие от ряда Фурье, преобразование Фурье раскладывает функцию не по дискретным частотам (набор частот ряда Фурье, по которым происходит разложение, вообще говоря, дискретный), а по непрерывным.
Давайте взглянем на то, как соотносятся коэффициенты ряда Фурье и результат преобразования Фурье, именуемый, собственно, спектром.
Небольшое отступление: спектр преобразования Фурье — в общем случае, функция комплексная, описывающая комплексные амплитуды соответствующих гармоник. Т.е., значения спектра — это комплексные числа, чьи модули являются амплитудами соответствующих частот, а аргументы — соответствующими начальными фазами. На практике, рассматривают отдельно амплитудный спектр и фазовый спектр.

Рис. 1. Соответствие ряда Фурье и преобразования Фурье на примере амплитудного спектра.
Легко видно, что коэффициенты ряда Фурье являются ни чем иным, как значениями преобразования Фурье в дискретные моменты времени.
Однако, преобразование Фурье сопоставляет непрерывной во времени, бесконечной функции другую, непрерывную по частоте, бесконечную функцию — спектр. Как быть, если у нас нет бесконечной во времени функции, а есть лишь какая-то записанная её дискретная во времени часть? Ответ на этот вопрос даёт дальнейшей развитие преобразования Фурье — дискретное преобразование Фурье (ДПФ).
Дискретное преобразование Фурье призвано решить проблему необходимости непрерывности и бесконечности во времени сигнала. По сути, мы полагаем, что вырезали какую-то часть бесконечного сигнала, а всю остальную временную область считаем этот сигнал нулевым.
Математически это означает, что, имея исследуемую бесконечную во времени функцию f(t), мы умножаем ее на некоторую оконную функцию w(t), которая обращается в ноль везде, кроме интересующего нас интервала времени.
Если «выходом» классического преобразования Фурье является спектр – функция, то «выходом» дискретного преобразования Фурье является дискретный спектр. И на вход тоже подаются отсчёты дискретного сигнала.
Остальные свойства преобразования Фурье не изменяются: о них можно прочитать в соответствующей литературе.
Нам же нужно лишь знать о Фурье-образе синусоидального сигнала, который мы и будем стараться отыскать в нашем спектре. В общем случае, это пара дельта-функций, симметричная относительно нулевой частоты в частотной области.

Рис. 2. Амплитудный спектр синусоидального сигнала.
Я уже упомянул, что, вообще говоря, мы рассматриваем не исходную функцию, а некоторое её произведение с оконной функцией. Тогда, если спектр исходной функции — F(w), а оконной W(w), то спектром произведения будет такая неприятная операция, как свёртка этих двух спектров (F*W)(w) (Теорема о свёртке).
На практике это означает, что вместо дельта-функции, в спектре мы увидим что-то вроде этого:

Рис. 3. Эффект растекания спектра.
Этот эффект именуют также растеканием спектра (англ. spectral leekage). А шумы, появляющиеся вследствие растекания спектра, соответственно, боковыми лепестками (англ. sidelobes).
Для борьбы с боковыми лепестками применяют другие, непрямоугольные оконные функции. Основной характеристикой «эффективности» оконной функции является уровень боковых лепестков (дБ). Сводная таблица уровней боковых лепестков для некоторых часто используемых оконных функций приведена ниже.
| Оконная функция | Уровень боковых лепестков (дБ) |
| Окно Дирихле (прямоугольное окно) | -13 дБ |
| Окно Ханна | -31.5 дБ |
| Окно Хэмминга | -42 дБ |
Основной проблемой в нашей задаче является то, что боковые лепестки могут маскировать другие гармоники, лежащие рядом.

Рис. 4. Отдельные спектры гармоник.
Видно, что при сложении приведённых спектров, более слабые гармоники как бы растворятся в более сильной.

Рис. 5. Чётко видна лишь одна гармоника. Нехорошо.
Другой подход к борьбе с растеканием спектра состоит в вычитании из сигнала гармоник, создающих это самое растекание.
То есть, установив амплитуду, частоту и начальную фазу гармоники, можно вычесть её из сигнала, при этом мы уберём и «дельта-функцию», соответствующую ей, а вместе с ней и боковые лепестки, порождаемые ей. Другой вопрос состоит в том, как же точно узнать параметры нужной гармоники. Недостаточно просто взять нужные данные из комплексной амплитуды. Комплексные амплитуды спектра сформированы по целым частотам, однако, ничто не мешает гармонике иметь и дробную частоту. В этом случае, комплексная амплитуда как бы расплывается между двумя соседними частотами, и точную её частоту, как и другие параметры, установить нельзя.
Для установления точной частоты и комплексной амплитуды нужной гармоники, мы воспользуемся приёмом, широко применяемым во многих отраслях инженерной практики – гетеродинирование.
Посмотрим, что получится, если умножить входной сигнал на комплексную гармонику Exp(I*w*t). Спектр сигнала сдвинется на величину w вправо.
Этим свойством мы и воспользуемся, сдвигая спектр нашего сигнала вправо, до тех пор, пока гармоника не станет ещё больше напоминать дельта-функцию (то есть, пока некоторое локальное отношение сигнал/шум не достигнет максимума). Тогда мы и сможем вычислить точную частоту нужной гармоники, как w0 – wгет, и вычесть её из исходного сигнала для подавления эффекта растекания спектра.
Иллюстрация изменения спектра в зависимости от частоты гетеродина показана ниже.

Рис. 6. Вид амплитудного спектра в зависимости от частоты гетеродина.
Будем повторять описанные процедуры до тех пор, пока не вырежем все присутствующие гармоники, и спектр не будет напоминать нам спектр белого шума.
Затем, надо оценить СКО белого шума. Хитростей здесь нет: можно просто воспользоваться формулой для вычисления СКО:
Автоматизируй это
Пришло время для автоматизации выделения гармоник. Повторим ещё разочек алгоритм:
1. Ищем глобальный пик амплитудного спектра, выше некоторого порога k.
1.1 Если не нашли, заканчиваем
2. Варируя частоту гетеродина, ищем такое значение частоты, при которой будет достигаться максимум некоторого локального отношения сигнал/шум в некоторой окрестности пика
3. При необходимости, округляем значения амплитуды и фазы.
4. Вычитаем из сигнала гармонику с найденной частотой, амплитудой и фазой за вычетом частоты гетеродина.
5. Переходим к пункту 1.
Алгоритм не сложный, и единственный возникающий вопрос — откуда же брать значения порога, выше которого будем искать гармоники?
Для ответа на этот вопрос, следует оценить уровень шума еще до вырезания гармоник.
Построим функцию распределения (привет, мат. cтатистика), где по оси абсцисс будет амплитуда гармоник, а по оси ординат — количество гармоник, не превышающих по амплитуде это самое значение аргумента. Пример такой построенной функции:

Рис. 7. Функция распределения гармоник.
Теперь построим еще и функцию — плотность распределения. Т.е., значения конечных разностей от функции распределения.

Рис. 8. Плотность функции распределения гармоник.
Абсцисса максимума плотности распределения и является амплитудой гармоники, встречающейся в спектре наибольшее число раз. Отойдем от пика вправо на некоторое расстояние, и будем считать абсциссу этой точки оценкой уровня шума в нашем спектре. Вот теперь можно и автоматизировать.
Практическая часть
Я не претендую на звание эксперта Java, и представленное решение может быть сомнительным как по части производительности и потреблению памяти, так и в целом философии Java и философии ООП, как бы я ни старался сделать его лучше. Написано было за пару вечеров, как proof of concept. Желающие могут ознакомиться с исходным кодом на GitHub.
Единственной сложностью стала генерация PDF отчёта по результатам анализа: PDFbox ну никак не хотел работать с кириллицей. К слову, не хочет и сейчас.
В проекте использовались библиотеки:
JFreeChart – отображение графиков
PDFBox – построение отчёта
JLatexMath – рендер Latex формул
В итоге, получилась довольно массивная программа (13.6 мегабайт), удобно реализующая поставленную задачу.
Есть возможность как вырезать гармоники вручную, так и доверить эту задачу алгоритму.
Что такое амплитудный спектр? Как связаны спектры периодического сигнала и одиночного импульса?
Классификация сигналов.
Что такое амплитудный спектр? Как связаны спектры периодического сигнала и одиночного импульса?
Амплитудным спектром называют набор амплитуд всех гармоник, который обычно представляют диаграммой в виде набора вертикальных линий, длины которых пропорциональны (в выбранном масштабе) амплитудным значениям гармонических составляющих, а место на горизонтальной оси определяется частотой (номером гармоники) данной составляющей.
4. Назначение и виды модуляции.
Модуляцией называется процесс управления одним или несколькими параметрами колебаний высокой частоты в соответствии с законом передаваемого сообщения. При модуляции происходит процесс наложения одного колебания (передаваемого сообщения) на другое колебание (несущая). Частота несущих колебаний должна быть на один и более порядков выше частоты модулирующего сигнала.
Сигнал при частотной и фазовой модуляции. билет №4
ЧМ-модулируемый параметр-частота гармонических колебаний, превращение которых зависит от времени и пропорц. значению модулируемого сигнала. ФМ-изменение в несущей начальной фазы.
Назначения и классификация линейных цепей.
Линейные цепи бывают пассивные и активные. Определяющим свойством линейных цепей является то, что их параметры и характеристики не зависят от амплитуды сигнала. Одна и та же цепь может быть линейной и нелинейной в зависимости от величины входного сигнала.
Прохождение сигнала через линейные цепи.
Электрические фильтры нижних частот.
Пропускает низкочастотные сигналы и не пропускает высокочастотные.
Полосовые фильтры.
Пропускает сигнал в определенном диапазоне частот.
Режекторные фильтры.
Для формировки режекторного фильтра надо включить фильтр НЧ и фильтр ВЧ параллельно.
— двойной Т-образный мост
Активные фильтры
Волноводы.
Волновод — искусственный или естественный канал, способный поддерживать распространяющиеся вдоль него волны, поля которых сосредоточены внутри канала или в примыкающей к нему области.
Основное свойство волновода — существование в нём дискретного (при не очень сильном поглощении) набора нормальных волн (мод), распространяющихся со своими фазовыми и групповыми скоростями. Почти все моды обладают дисперсией, то есть их фазовые скорости зависят от частоты и отличаются от групповых скоростей.
Объёмные резонаторы.
Объёмный резона́тор — устройство, основанное на явлении резонанса, в котором вследствие граничных условий возможно существование на определенных длинах волн добротных колебаний в виде бегущей или стоячей волны. В соответствии с уравнениями Максвелла переменное электрическое поле порождает переменное магнитное поле, и наоборот. Между электрическим и магнитным полями происходит непрерывный обмен энергией. Если каким-либо образом ограничить некоторый объём пространства отражающими стенками, препятствующими потере энергии из этого объёма за счет излучения, то в этом объёме на некоторых длинах волн, определяемых размерами устройства можно возбудить электромагнитные колебания. Если полый резонатор образован металлическими стенками, то он также часто называется закрытым резонатором. Объёмные СВЧ резонаторы могут быть также заполнены диэлектриком. Существуют также открытые диэлектрические резонаторы, без металлических стенок, в которых волна отражается от границ диэлектрика за счет эффекта полного внутреннего отражения — резонаторы с модами «шепчущей галереи». В связи с тем, что электрические и магнитные поля почти не выходят за пределы границ объёмного резонатора, их добротность чрезвычайно высока (10000 и более).
Генерация ВЧ колебаний.
Генератор высокочастотных колебаний на транзисторе
Первая четверть периода. Положительно заряженная пластина конденсатора, соединенная с коллектором, разряжается. Ток в колебательном контуре возрастает до максимального значения. В катушке связи возникает индукционный ток такого направления, что база имеет отрицательный потенциал относительно эмиттера. Переходы база — коллектор и эмиттер — база прямые. Транзистор открыт. Энергия от источника поступает через транзистор в колебательный контур (ключ замкнут).
Вторая четверть периода. Ток в контуре убывает. Верхняя пластина заряжается отрицательно. В катушке связи ток меняет направление. На базе положительный потенциал. Переход коллектор—база обратный. Тока в цепи нет (ключ разомкнут).
Третья четверть периода. Конденсатор разряжается. Ток растет до максимального значения, направлен от нижней пластины к верхней. В катушке связи ток направлен так, что база получает положительный потенциал. Переход база — коллектор обратный. Тока в цепи нет (ключ разомкнут).
Четвертая четверть периода. Ток в контуре, не меняя направления, убывает. Верхняя пластина заряжается положительно.
В катушке связи ток меняется по направлению. Заряд на базе отрицательный. Переходы база — коллектор и эмиттер — база прямые. Энергия поступает от источника в колебательный контур (ключ замкнут).
Таким образом, происходят незатухающие электромагнитные колебания за счет поступления энергии от источника в колебательный контур в течение 1/2 Т.
Амплитудная модуляция.
Частотный модулятор.
Воздействие на частоту переменного напряжения наиболее просто осуществить в месте его возникновения, поэтому частотные модуляторы, как правило, объединены с источником модулируемого напряжения.
В низкочастотной электронике частоту формируемого генератором напряжения изменяют главным образом путем изменения параметров частотоопределяющих элементов автогенератора: емкости, индуктивности и сопротивлений.
Амплитудный демодулятор.
Амплитудным детектором (АД) называется устройство, предназначенное для получения на выходе напряжения, изменяющегося в соответствии с законом модуляции амплитуды входного гармонического сигнала. Процесс детектирования амплитудно-модулированных (АМ) сигналов вида
где ua(t)=Uc[1+max(t)], ma £ 1 – коэффициент глубины модуляции; Uc – амплитуда несущего колебания с частотой ωc, заключается в воспроизведении модулирующего сообщения x(t) с наименьшими искажениями. Спектр сообщения x(t) сосредоточен в области низких частот (частот модуляции), а спектр сигнала uc (t) – в области частоты ωc, значение которой обычно намного превышает значение наивысшей частоты модуляции. Преобразование спектра при демодуляции возможно только в устройствах, выполняющих нелинейное или параметрическое преобразование входного сигнала uc(t).
Частотный демодулятор.
Демодуляторы ЧМ сигналов также могут быть реализованы как на цифровых, так и на аналоговых устройствах. Один из вариантов аналогового демодулятора использует представление ЧМ сигнала в виде суммы двух АМ сигналов. Такая схема получила название двухполосной схемы приема по огибающей (рис. 2.6). Входной сигнал преобразуется усилителем-ограничителем УО в прямоугольные импульсы (рис. 2.9, б).
В формирователе импульсов сброса ФИС выделяются короткие импульсы, соответствующие каждому периоду входного сигнала из импульсов, изображенных на рис. 2.9, б. Короткие импульсы подаются поочередно на делители частоты (рис. 2.9, в и г), устанавливая их в начальное состояние (обозначено точками на рис. 2.9, д и е). Импульсы на выходе делителей при приеме средней частоты fcp изображены на рис. 2.9, д и е. В этом случае между сигналами на выходе делителей сдвиг по фазе равен четверти периода, причем знак сдвига фаз меняется после поступления каждого импульса сброса. Сигналы с выходов делителей поступают на вход фазового детектора ФД (выполненного в виде сумматора по mod2), на выходе которого возникает последовательность импульсов (рис. 2.9,ж), ширина каждого из которых зависит от соотношения фаз сигналов на выходах делителей.
Классификация сигналов.
Что такое амплитудный спектр? Как связаны спектры периодического сигнала и одиночного импульса?
Амплитудным спектром называют набор амплитуд всех гармоник, который обычно представляют диаграммой в виде набора вертикальных линий, длины которых пропорциональны (в выбранном масштабе) амплитудным значениям гармонических составляющих, а место на горизонтальной оси определяется частотой (номером гармоники) данной составляющей.
4. Назначение и виды модуляции.
Модуляцией называется процесс управления одним или несколькими параметрами колебаний высокой частоты в соответствии с законом передаваемого сообщения. При модуляции происходит процесс наложения одного колебания (передаваемого сообщения) на другое колебание (несущая). Частота несущих колебаний должна быть на один и более порядков выше частоты модулирующего сигнала.
Амплитудно-частотная характеристика (АЧХ). Спектр сигнала.
При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы и как с ними работать? В этом нам и предстоит сегодня разобраться 🙂 Кроме того, мы рассмотрим важнейшее понятие — амплитудно-частотную характеристику (АЧХ) сигналов.
Гармонические и негармонические сигналы.
Здесь A — амплитуда сигнала, w — циклическая частота, а \phi — начальная фаза. Вы спросите — а как же синус? Разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sin\alpha = cos(\frac<\pi><2>\medspace-\medspace \alpha) — то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний 🙂
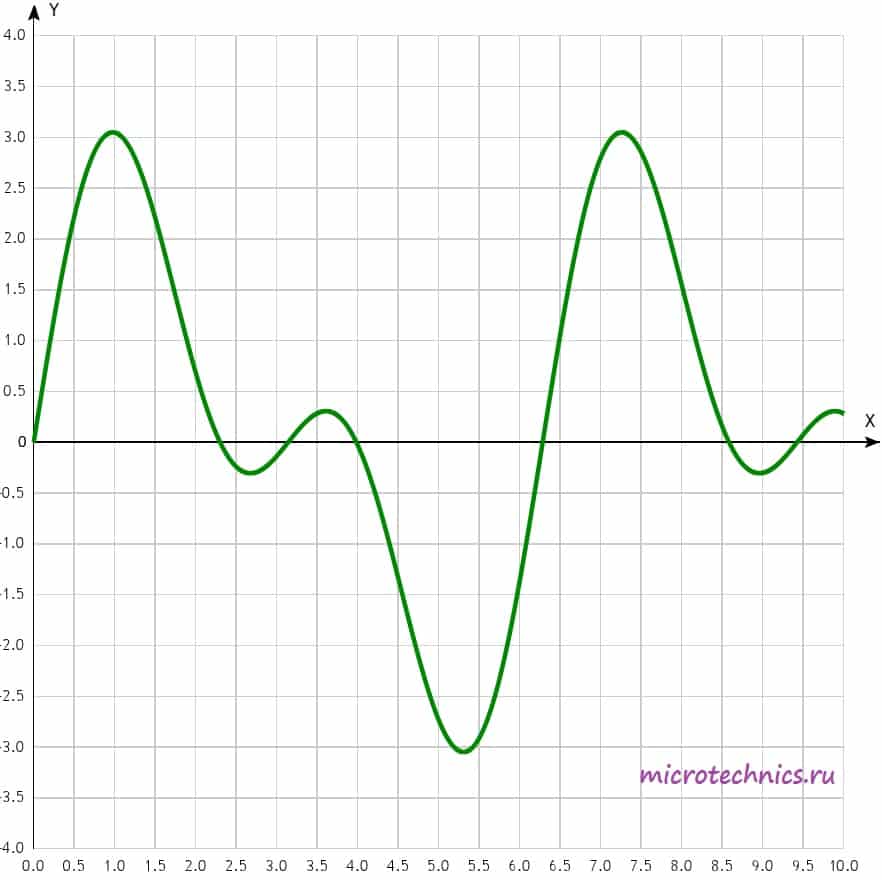
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
Как видите, несмотря на «нестандартную» форму, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть методики состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что давайте рассмотрим практический пример и разберемся чуть подробнее 🙂 Для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
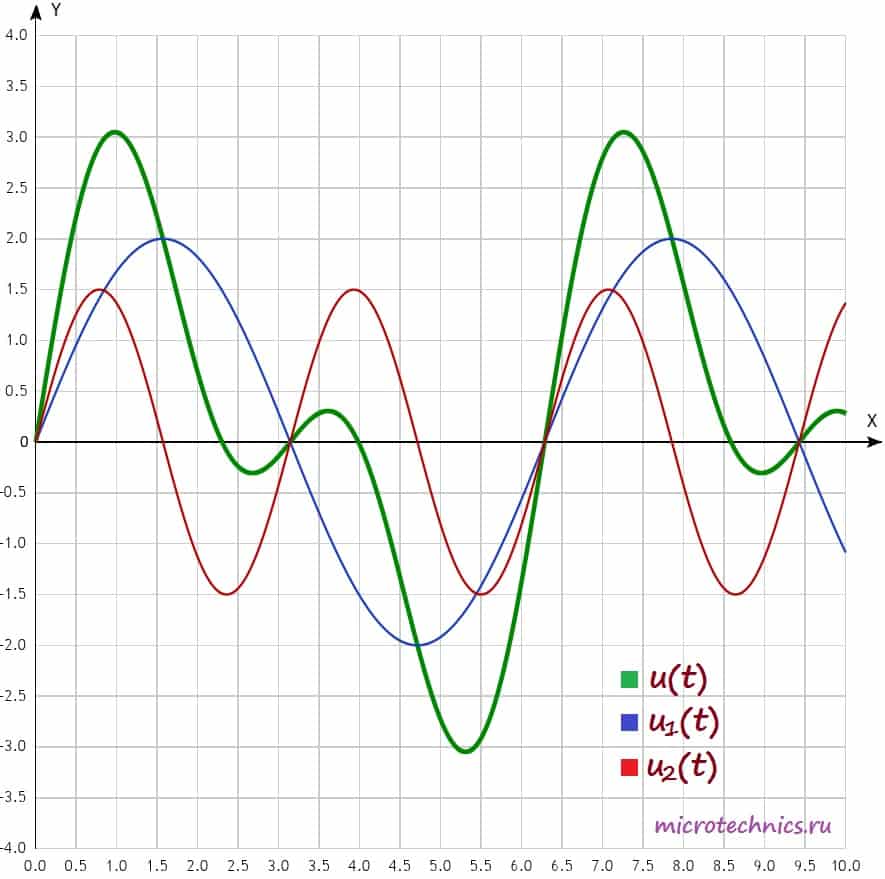
Давайте изобразим все эти сигналы на одном графике:
В этой формуле U_k — амплитуда, а \phi_k — начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и видим в этой формуле 🙂 U_0 — это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите — среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0.
Амплитудный спектр сигнала.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:
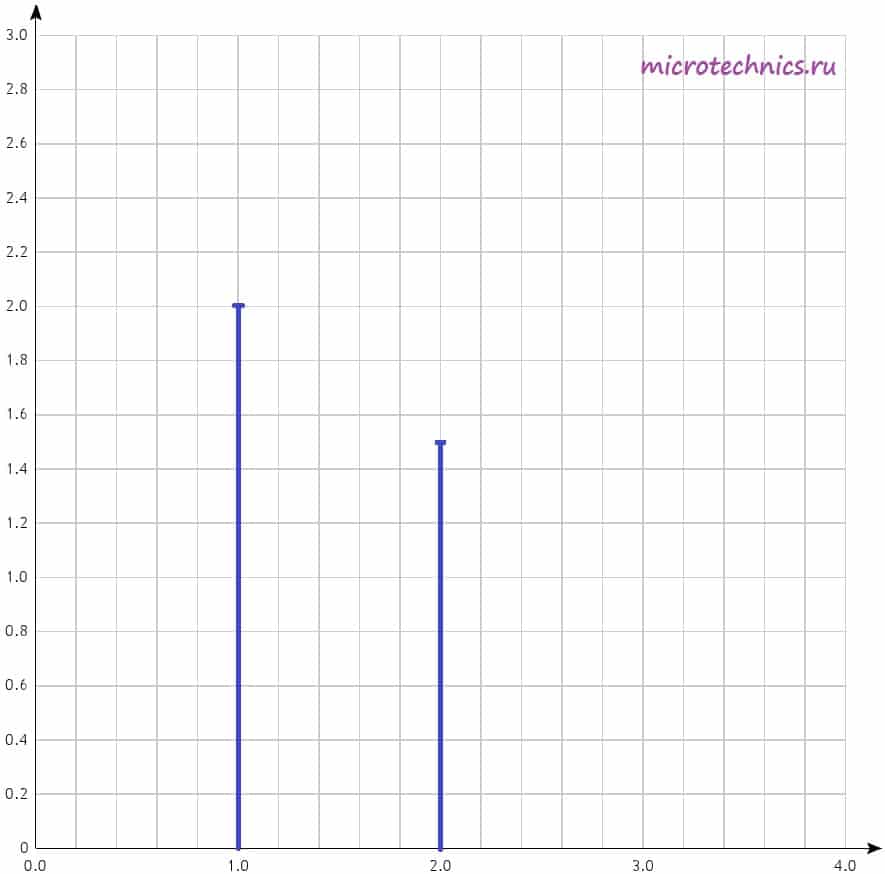
Давайте рассмотрим амплитудный спектр поподробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
По горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси — амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались! Давайте перейдем к следующей теме сегодняшней статьи — к понятию амплитудно-частотной характеристики.
Амплитудно-частотная характеристика (АЧХ).
АЧХ является важнейшей характеристикой многих цепей и устройств — фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Что же она показывает?
АЧХ — это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но нас сейчас интересует, в первую очередь, аудио-сигнал, и выглядит он следующим образом:
Как видите, ни о какой периодичности здесь не идет и речи! Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи 🙂 Просто примем тот факт, что они позволяют нам осуществить такое преобразование с аудио-сигналом.
Соответственно, мы можем построить диаграмму амплитудного спектра звукового сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте обсудим этот момент чуть поподробнее…
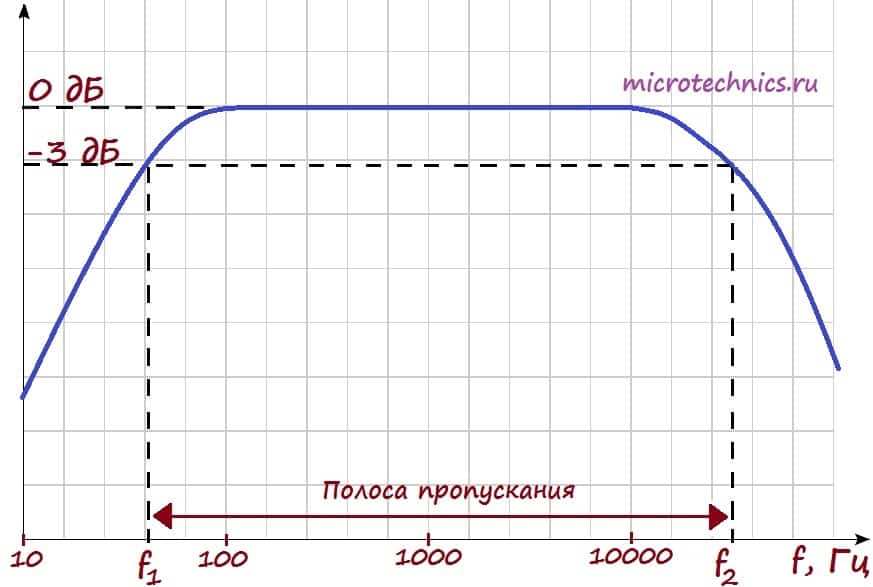
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:
Разберемся поэтапно, что же тут изображено… Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы откладываем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.
По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.
Практические примеры АЧХ аудио-устройств.
Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:
Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье 🙂
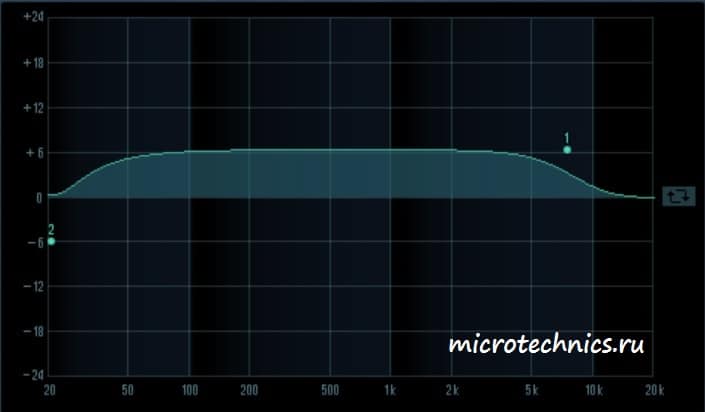
В завершении статьи посмотрим на пару АЧХ, полученных в программном эквалайзере:
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.
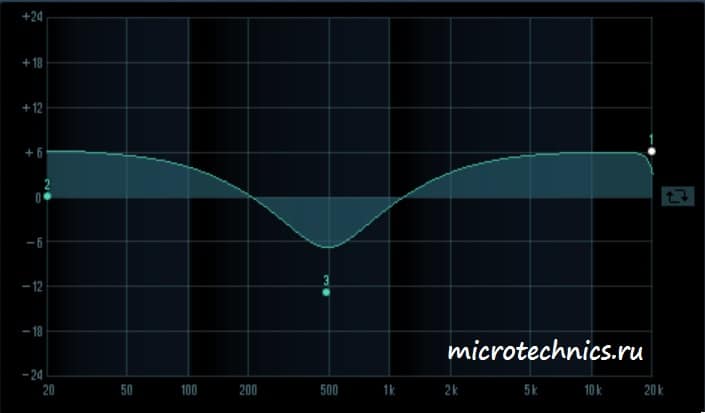
А здесь ситуация совсем другая — низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.
А здесь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов 🙂
На этом мы заканчиваем нашу сегодняшнюю статью… Спасибо за внимание и ждем вас на нашем сайте снова!