что такое амплитуда гармонических колебаний

Что такое амплитуда гармонических колебаний

Ускорение — вторая производная координаты по времени.

где х» — вторая производная координаты по времени.

При свободных колебаниях координата х изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.

Гармонические колебания

Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями.

Амплитуда колебаний

Амплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия.

Амплитуда определяется начальными условиями, а точнее энергией, сообщаемой телу.

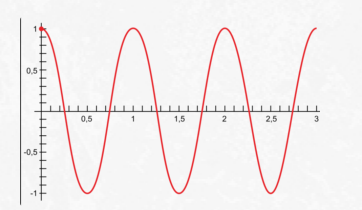
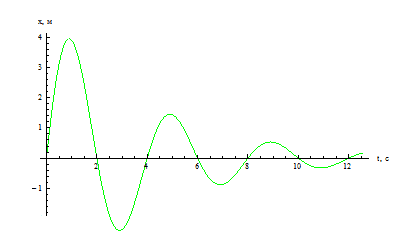
График зависимости координаты тела от времени представляет собой косинусоиду.

Тогда уравнение движения, описывающее свободные колебания маятника:

Период и частота гармонических колебаний.

При колебаниях движения тела периодически повторяются.
Промежуток времени Т, за который система совершает один полный цикл колебаний, называется периодом колебаний.

В Международной системе единиц (СИ) единица частоты называется герцем (Гц) в честь немецкого физика Г. Герца.

Число колебаний за 2π с равно:

Величина ω₀ — это циклическая (или круговая) частота колебаний.
Через промежуток времени, равный одному периоду, колебания повторяются.

Частоту свободных колебаний называют собственной частотой колебательной системы.
Часто для краткости циклическую частоту называют просто частотой.

Зависимость частоты и периода свободных колебаний от свойств системы.

1. для пружинного маятника

Собственная частота колебаний пружинного маятника равна:

Она тем больше, чем больше жесткость пружины k, и тем меньше, чем больше масса тела m.
Жесткая пружина сообщает телу большее ускорение, быстрее меняет скорость тела, а чем тело массивнее, тем медленнее оно изменяет скорость под влиянием силы.

Период колебаний равен:

Период колебаний пружинного маятника не зависит от амплитуды колебаний.

2. для нитяного маятника

Собственная частота колебаний математического маятника при малых углах отклонения нити от вертикали зависит от длины маятника и ускорения свободного падения:

Период же этих колебаний равен:

Период колебаний нитяного маятника при малых углах отклонения не зависит от амплитуды колебаний.

Период колебаний возрастает с увеличением длины маятника. От массы маятника он не зависит.

Чем меньше g, тем больше период колебаний маятника и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут за сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета (высота 200 м). И это только за счет уменьшения ускорения свободного падения с высотой.

Источник

Гармонические колебания

теория по физике 🧲 колебания и волны

Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.

Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.

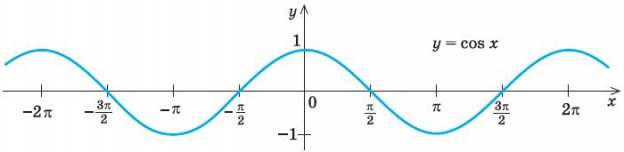
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.

Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.

Уравнение движения гармонических колебаний

Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:

Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.

Тогда первая производная примет вид:

Вторая производная примет вид:

Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:

Само уравнение движения, описывающего свободные колебания, примет вид:

Период и частота гармонических колебаний

Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:

Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.

Зависимость частоты и периода свободных колебаний от свойств системы

Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:

Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:

Отсюда период и частота колебаний соответственно равны:

Отсюда период и частота колебаний математического маятника соответственно равны:

Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.

Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.

Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.

Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?

Искомое число колебаний равно отношению времени к периоду колебаний:

Период колебаний для математического маятника определяется формулой:

Фаза колебаний

Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).

Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.

Можно изобразить на графике зависимость координаты колеблющейся точки не от времени, а от фазы. В этом случае графиком также будет являться косинусоида (или синусоида), но аргументом функции будет не время (период), а фаза, выражающаяся в радианах (см. рис.).

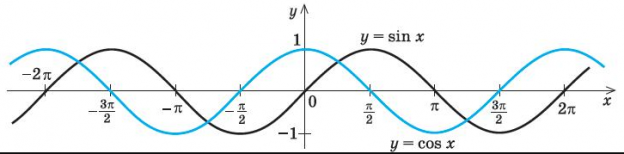
Выбор закона зависит от условий задачи. Если колебания начинаются с того, что тело выводят из положения равновесия и отпускают, удобнее пользоваться косинусоидальным законом, поскольку в начальный момент времени косинусоида показывает, что это тело отклонено максимально, а не находится в положении равновесия. Если для того чтобы начались колебания, совершают толчок, удобнее использовать синусоидальный закон, так как начальному моменту времени на синусоиде соответствует положение равновесия.

Превращение энергии при гармонических колебаниях

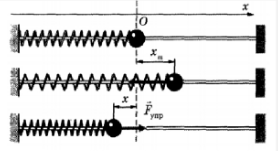
Чтобы описать превращения энергии при гармонических колебаниях, условимся, что силой трения будем пренебрегать. Для описания обратимся к рисунку ниже.

Точке О на рисунке соответствует положение равновесия шарика. Если его оттянуть на расстояние x_max, равное амплитуде, пружина получит потенциальную энергию, которая примет в этом положении максимальное значение, равное:

Когда шарик отпускают, возникает сила упругости, под действием которой шарик устремляется влево. По мере уменьшения расстояния между точкой максимального отклонения и положением равновесия уменьшается и потенциальная энергия. Но в это время увеличивается кинетическая энергия шарика. Когда шарик проходит через положение равновесия в первый раз, его потенциальная энергия становится равной нулю, а кинетическая энергия обретает максимальное значение (скорость в этот момент времени тоже максимальна):

После прохождения точки О расстояние между шариком и положением равновесия снова увеличивается, и потенциальная энергия растет. Кинетическая же энергия при этом уменьшается. А в крайнем положении слева она становится равной нулю, в то время как потенциальная энергия снова примет максимальное значение.

Так как мы условились пренебрегать трением, данную колебательную систему можно считать изолированной. Тогда в ней должен соблюдаться закон сохранения энергии. Согласно ему, полная механическая энергия системы равна:

В действительности свободные колебания всегда затухают, так как в колебательной системе действует сила трения. И часть механической энергии рассеивается в виде тепла. Пример графика затухающих колебаний выглядит следующим образом:

Пример №2. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. Найдите отношение кинетической энергии груза к его потенциальной энергии системы в момент, когда груз находится в точке, расположенной посередине между крайним положением и положением равновесия.

Так как груз находится посередине между крайним положением и положением равновесия, его координата равна половине амплитуды:

В это время потенциальная энергия груза будет равна:

Согласно закону сохранения энергии, кинетическая энергия в это время равна:

Полная механическая энергия системы равна максимальной потенциальной энергии:

Тогда кинетическая энергия равна:

Следовательно, отношение кинетической энергии к потенциальной будет выглядеть так:

Резонанс

Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называют вынужденными.

Работы силы над такой системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.

Особый интерес вызывают вынужденные колебаний в системе, способной совершать свободные колебания. Примером такой системы служат качели. Их не получится отклонить на большой угол всего лишь одним толчком. Если их толкать то в одну, то в другую сторону, тоже ничего не получится. Но если подталкивать качели всякий раз, как они сравниваются с нами, можно раскачать их очень сильно. При этом не нужно прикладывать большую силу, но на это понадобится время. Причем после каждого такого толчка амплитуда колебаний качелей будет увеличиваться до тех пор, пока не достигнет своего максимального значения. Такое явление называется резонансом.

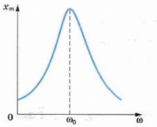
Резонанс — резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний.

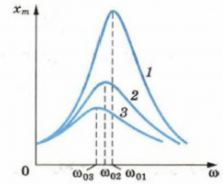
Графически явление резонанса можно изобразить как резкий скачок графика вверх (см. рис. выше). Причем высота «зубца», или амплитуда колебаний, будет зависеть от величины сил трения. Чем больше сила трения, тем меньше при резонансе возрастает амплитуда вынужденных колебаний. Это можно продемонстрировать графиками на рисунке ниже. Графику 1 соответствует минимальное трение, графику 3 — максимальное.

На явлении резонанса основан принцип работы частотомера — устройства, предназначенного для измерения частоты переменного тока. Он состоит из набора упругих пластин, которые закреплены на одной планке. Каждая пластина обладает определенной собственной частотой колебаний, которая зависит от упругих свойств, длины и массы. Собственные колебания пластин известны. Под действием электромагнита планка, а вместе с ней и пластины совершают вынужденные колебания. Но лишь та пластина, собственная частота которой совпадает с частотой колебаний планки, будет иметь большую амплитуду колебаний. Таким образом, определяется частота переменного тока.

Пример №3. Автомобиль движется по неровной дороге, на которой расстояние между буграми равно приблизительно 8 м. Период свободных колебаний автомобиля на рессорах 1,5 с. При какой скорости автомобиля его колебания в вертикальной плоскости станут особенно заметными?

Колебания автомобиля в вертикальной плоскости будут заметны тогда, когда частота наезда на бугры сравняется с частотой свободных колебаний автомобиля на рессорах. Поскольку частота обратно пропорциональна периоду, можно сказать, что резонанс будет достигнут тогда, когда автомобиль будет наезжать на бугры каждые 1,5 секунды. Зная расстояние между буграми и время, можем вычислить скорость:

Источник

Амплитуда, период, частота колебаний.

Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша­рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах, санти­метрах и т. д. На графике колебаний амплитуда определяется как макси­мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша­ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Другими словами, период колебаний (Т) — это время, за которое совершается одно полное ко­лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы­рем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей­ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес­ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю­щихся величин, например, для затухающих колебаний.

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.

Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

.

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

.

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Источник

Механические колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Гармонические колебания.

Выясним смысл входящих в эту формулу величин.

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Рис. 2. Закон косинуса

Рис. 3. Закон синуса

Уравнение гармонических колебаний.

Теперь дифференцируем полученное равенство (4) :

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Пружинный маятник.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4 ). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

Тогда соотношение (8) принимает вид:

Циклическая частота колебаний пружинного маятника, таким образом, равна:

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

Математический маятник.

Рис. 5. Математический маятник

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

Если маятник занимает положение как на рисунке (т. е. 0′ alt=’x>0′ /> ), то:

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

Итак, при любом положении маятника имеем:

Следовательно, циклическая частота колебаний математического маятника равна:

Отсюда период колебаний математического маятника:

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6 ).

Рис. 6. Затухающие колебания

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Рис. 7. Резонанс

Источник